Положительный ряд сходится тогда и только тогда, когда последовательность его частичных сумм ограничена.

Стремится к нулю при : .

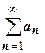сходится 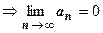. Обратное неверно. Пример – гармонический ряд.

Доказательство. Если , то и , но , следовательно .

С проверки выполнения условия 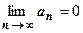надо начинать решение любой задачи на исследование сходимости ряда: если это условие не выполняется, то ряд заведомо расходится. Это условие необходимо, но не достаточно для сходимости ряда: общий член гармонического ряда (18.1.2) 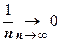, однако этот ряд расходится.

Введём понятие остатка ряда.

Определение. Остатком ряда (18.2.1) после n-го члена называется ряд .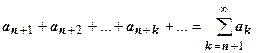

18.1.2.2. Если сходится ряд (18.2.1), то сходится любой его остаток, Обратно, если сходится какой-нибудь остаток ряда, то сходится и сам ряд.

Доказательство. Пусть 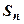- частичные суммы ряда (18.2.1); обозначим k-ую частичную сумму остатка 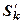: 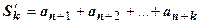. Тогда 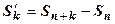. Устремим 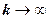, считая n фиксированным числом. Ряд (18.2.1) сходится, т.е. существует конечный 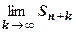, следовательно существует конечный предел 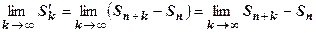, т.е. остаток сходится. Обратное утверждение доказывается также. Так как 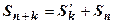, то из существования конечного предела 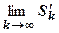следует существование конечного предела 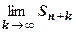, т.е. из сходимости остатка следует сходимость ряда.

Житейский вывод из этого свойства: отбрасывание конечного числа начальных членов ряда или добавление в его начало нескольких новых членов не влияет на сходимость ряда.

18.1.2.3. Если ряд сходится, то сумма его остатка после n-го члена стремится к нулю при .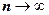

Доказательство. Пусть S - сумма исходного ряда (18.2.1), 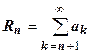- сумма его остатка. Из равенства 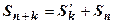следует 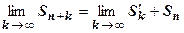, т.е. 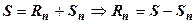. Отсюда .

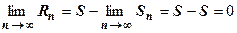Здесь тоже можно сделать житейский вывод. Из предыдущего свойства следует, что сходимость ряда определяется сходимостью его остатка, т.е. хвостом ряда, а сумма S ряда, как следует из равенства 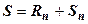, определяется пределом 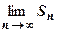, т.е. началом ряда.

18.1.2.4. Если все члены сходящегося ряда умножить на одно и то же число с, то сходимость ряда сохранится, а сумма умножится на с.

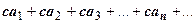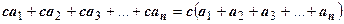Доказательство. Частичная сумма ряда есть ; по свойству предела .

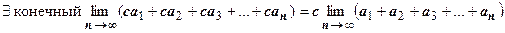18.1.2.5. Два сходящихся ряда 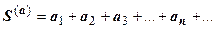и 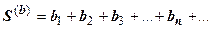можно почленно складывать и вычитать; ряд 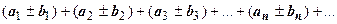также сходится, и его сумма равна .

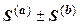Доказательство и этого свойства - прямое следствие свойств пределов для частичных сумм: .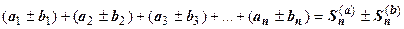

18.1.3. Сходимость рядов с положительными членами (положительных рядов). Термином "положительный ряд" мы будем называть числовой ряд с неотрицательными членами: 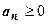для 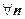. Для таких рядов частичная сумма 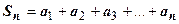является возрастающей функцией аргумента n. Монотонно возрастающая функция имеет конечный предел тогда и только тогда, когда она ограничена сверху, поэтому сразу сформулируем признак сходимости положительных рядов:

Положительный ряд сходится тогда и только тогда, когда последовательность его частичных сумм ограничена.

В случае, когда последовательность частичных сумм положительного ряда неограничена, будем говорить, что его сумма равна .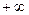

При доказательстве расходимости гармонического ряда мы, по существу, доказали, что последовательность его частичных сумм неограничена. В качестве другого примера прямого применения этого признака рассмотрим ряд Дирихле (или обобщённый гармонический ряд)

. (18.3.1)

Если s<1, то 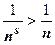, и, так как частичные суммы 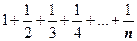неограничены, то суммы 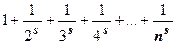и подавно неограничены, т.е. при s<1 ряд (18.3.1) расходится. Пусть теперь s>1. Как и для гармонического ряда сгруппируем члены в частичной сумме по степеням числа 2: …+ .

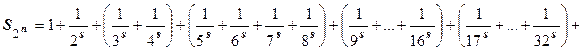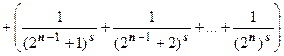Структура каждой скобки: 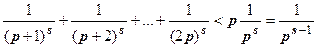, поэтому 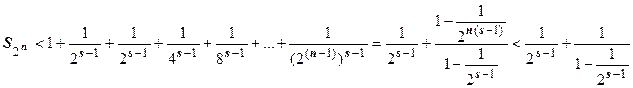(мы воспользовались формулой для частичной суммы геометрической прогрессии). Последовательность ограничена; ряд сходится.

Итак, ряд Дирихле (18.3.1) сходится при s>1, расходится при s 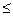1. Дальше мы дадим более простое доказательство этого факта, основанное на интегральном признаке Коши.