Разложение колебаний по системам
ОРТОГОНАЛЬНЫХ ФУНКЦИЙ
Бесконечную систему функций 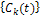 называют ортогональной на отрезке
называют ортогональной на отрезке 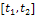 , если выполняются равенства
, если выполняются равенства
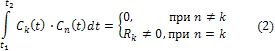
причем n=0, 1, 2,...и k=0, 1,2, ...
Первое из равенств означает попарную ортогональность функций системы, второе – то, что никакая из функций не равна тождественно нулю.
Величина 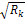 называется нормойфункции
называется нормойфункции 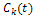
Если все 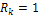 , система функций является ортонормированной.
, система функций является ортонормированной.
Простейшем примером системы, ортогональной на любом отрезке длиной 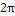 может служить совокупность тригонометрических функций кратных аргументов
может служить совокупность тригонометрических функций кратных аргументов
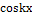 и
и 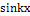 , при k=0,1,2,…. (3)
, при k=0,1,2,…. (3)
Заданное (аналитически или графически) колебание 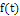 можно
можно
разложить в ряд
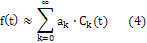
по упорядоченной системе ортогональных функций 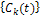 , если возможно подобрать такую совокупность постоянных коэффициентов
, если возможно подобрать такую совокупность постоянных коэффициентов 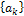 , что разность между f(t )и суммой конечного числа членов ряда
, что разность между f(t )и суммой конечного числа членов ряда
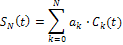
будет достаточна, мала. Предполагается, что область задания колебания f(t ) находится внутри отрезка ортогональности 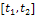 .
.
Одним из возможных критериев качества разложения (сходимости) является интегральная (усредненная) оценка квадрата этой разности:
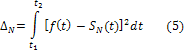
Если при увеличении количества N суммируемых членов ряда  монотонно убывает и может быть сделана сколь угодно малой, то систему ортогональных функций
монотонно убывает и может быть сделана сколь угодно малой, то систему ортогональных функций 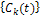
 считают полной, а ряд (4) называют сходящимся в среднем к функции f(t). При такой сходимости функция
считают полной, а ряд (4) называют сходящимся в среднем к функции f(t). При такой сходимости функция 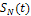
 аппроксимирующая заданную f(t)
аппроксимирующая заданную f(t)  , может кратковременно значительно отклоняться от f(t)
, может кратковременно значительно отклоняться от f(t)  , и существенным является лишь интегральный эффект. Кстати, для большинства задач электротехники вполне достаточно сходимости со средним, которая всегда имеет место для колебаний конечной энергии.
, и существенным является лишь интегральный эффект. Кстати, для большинства задач электротехники вполне достаточно сходимости со средним, которая всегда имеет место для колебаний конечной энергии.
Для определения значений коэффициентов 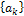
 , обеспечивающих минимальную величину
, обеспечивающих минимальную величину  , приравняем к нулю частные производные по этим коэффициентам
, приравняем к нулю частные производные по этим коэффициентам
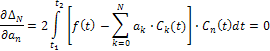
и получим систему из N уравнений, так как n=1, 2,…N. Осуществив преобразования каждого уравнения этой системы с учётом свойства ортогональности (2), установим, что
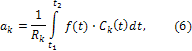
Ряд (4), в котором коэффициенты определены по формуле (6) , называют обобщенным рядом Фурье по системе функций 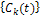
 . Поскольку при этом
. Поскольку при этом 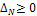
 , из выражения (5) можно получить важную "энергетическую" оценку для функций f(t)с интегрируемым квадратом
, из выражения (5) можно получить важную "энергетическую" оценку для функций f(t)с интегрируемым квадратом
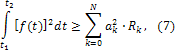
которую называют неравенством Бесселя. Равенство здесь имеет место в пределе (при 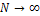 ), если система функций
), если система функций 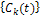 полна.
полна.
Важной задачей математического анализа является выяснение условий, когда обобщенный ряд Фурье сходится к f(t) в обычном
смысле, т.е. поточечно:
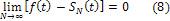
В частности, при использовании ортогональной системы тригонометрических функций ответ на этот вопрос дает теорема Дирихле.
Пусть f(t) в пределах отрезка 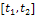
 ограниченной длины удовлетворяет так называемым условиям Дирихле:
ограниченной длины удовлетворяет так называемым условиям Дирихле:
-Отрезок 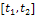
 можно разбить на конечное число частей так, что внутри каждой части f(t) монотонна и непрерывна;
можно разбить на конечное число частей так, что внутри каждой части f(t) монотонна и непрерывна;
-Во всех точках нарушения непрерывности существуют пределы слева  и справа
и справа 
Тогда ряд (4) сходится и имеет место равенство:
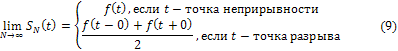
Следовательно, во всех точках непрерывности выражение (4) переходит в точное равенство.
Теперь возможен иной способ получения формулы (6). Умножим обе части выражения (4) на С (t)  и произведем интегрирование:
и произведем интегрирование:
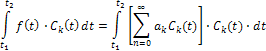
В силу свойств ортогональности, в правой части останется только одно
Слагаемое 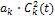 . Откуда следует (6).
. Откуда следует (6).
Если функциюf(t) продолжить на всю осьпериодически с периодом Т=t1– t2, то утверждение теоремы Дирихле будет справедливо для всех 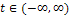 .
.
Как правило, функцииf(t), описывающие реальные колебания, которые встречаются в электротехнике и электронной технике, удовлетворяют условиям Дирихле, и специальных исследований не требуется.
Выбор наиболее рациональной ортогональной системы функций зависит от цели, преследуемой при разложении сложной функции в ряд. В задачах аппроксимации колебаний основным требованием является обеспечение наиболее быстрой сходимости ряда, т.е.наименьшего числа N членов рада (при заданной допустимой погрешности). Применяются разнообразные ортогональные системы функции: полиномы Чебышева, Эрмита, Лежандра, функции Бесселя и другие.
Однако часто решающими при выборе система функции являются простота физического воспроизведения (генерирования) этих функций и удобство последующего использования их при решении других задач. Этим требованиям удовлетворяет система основных тригонометрических (гармонических) функций. Поэтому гармонический анализ получил широкое распространение во всех отраслях современней науки к техники.
