Ранг матрицы. Теорема Кронекера-Капелли.

Основные определения и понятия

Совокупность уравнений вида

(1),

называется системой т линейных уравнений с п неизвестными. Здесь а_ij – коэффициенты при неизвестных, х_i – неизвестные, b_j – свободные члены системы (i = 1,2,…, n, j = 1,2,…, m).

Если из коэффициентов системы составить матрицы:

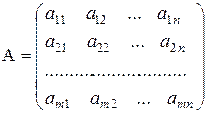– основную матрицу системы,

Х= – матрицу-столбец неизвестных,

В = 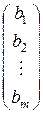– матрицу-столбец свободных членов,

то система (1) может быть записана в виде равносильного ей матричного уравненияАХ = В.

Наряду с перечисленными матрицами для СЛУ (1) рассматривают матрицу

,

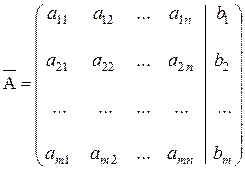которую называют расширенной матрицей системы.

Определение 1.

Решениемсистемы (1) называется упорядоченная совокупность п действительных чисел a₁, a₂, ..., a_п, при подстановке которых в систему вместо х₁, х₂,…, х_n соответственно, каждое уравнение этой системы обращается в верное равенство.

Система называется совместной, если она имеет хотя бы одно решение, в противном случае система несовместна.

Если система линейных уравнений имеет единственное решение, то её называют определённой, если совместная система имеет более одного решения, то её называют неопределённой.

Исследовать систему – значит, выяснить

1) является ли эта система совместной?

2) если система совместна, сколько решений она имеет (т.е. определенная система или неопределенная)?

Решить систему – значит, исследовать ее и в случае совместности найти все решения этой системы.

С помощью перечисленных выше матриц можно исследовать и решать заданную СЛУ.

Рассмотрим частные виды СЛУ.

Решение «квадратных» СЛУ.

Пусть т = п, т.е. число уравнений системы равно числу ее неизвестных

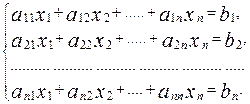(2)

В этом случае основная матрица системы (2) есть квадратная матрица, поэтому такие системы также называют «квадратными». Рассмотрим методы исследования и решения таких систем.

I. Матричный метод.

Как уже отмечалось, с помощью матриц

, , ,

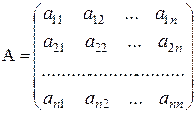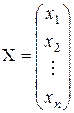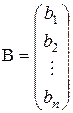система (2) может быть записана в виде матричного уравнения АХ = В. Если матрица А невырожденная, то для нее существует обратная матрица А^–1. Умножая обе части равенства АХ = В на А^–1 слева, получим

(А^–1А)Х = А^–1В Þ ЕХ = А^–1В Þ Х = А^–1В.

Эта формула и выражает суть матричного метода решения «квадратной» системы.

Таким образом, если основная матрица «квадратной» СЛУ невырожденная, то система совместна и, чтобы найти решение этой системы, достаточно обратную матрицу для основной матрицы системы умножить слева на столбец свободных членов. При этом, т.к. обратная матрица для заданной единственна, то СЛУ имеет единственное решение.

Пример

Найти решение системы линейных уравнений

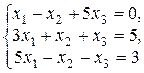
с помощью обратной матрицы.

Решение. Рассмотрим основную матрицу системы

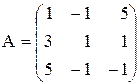
и вычислим её определитель:

.

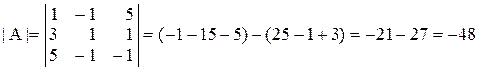Так как , то заданная система совместна и имеет единственное решение, а матрица А имеет обратную матрицу 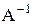. Решение системы найдем по формуле

,

где Х= 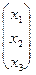- матрица-столбец неизвестных, В= 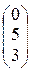– матрица-столбец свободных членов данной системы. Матрица 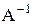для матрицы А была найдена в примере 1.6:

.

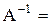
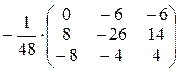Тогда решение данной системы имеет вид

Х=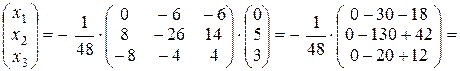

.

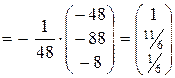Отсюда .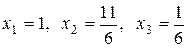

Проверка: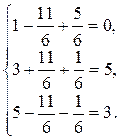

Таким образом, тройка чисел 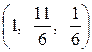является решением заданной системы.

Заметим, что если основная матрица СЛУ вырожденная, то вопрос о совместности системы остается открытым, но матричный метод применять уже нельзя.

II. Правило Крамера.

В основе метода лежит теорема:

Теорема (Крамера)

Если в «квадратной» СЛУ определитель |A| основной матрицы системы отличен от нуля, то система имеет единственное решение и неизвестные х_i могут быть найдены по формулам

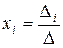, (3)

где D = |A| ¹ 0 – определитель основной матрицы системы, а Di - определитель, получаемый из определителя D заменой его i-го столбца столбцом свободных членов.

Определитель D = |A| называют главным определителем системы, определители Di – побочными.

Доказательство: Так как D = |A| ¹ 0, то Х = А^–1В, откуда получаем

Х= = . =

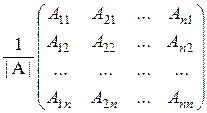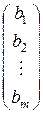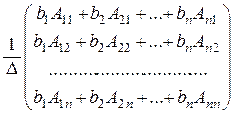= , откуда .

Рассмотрим определитель

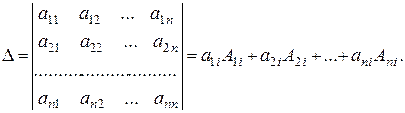
Если в этом определителе заменить i-й столбец столбцом свободных членов, то получим определитель

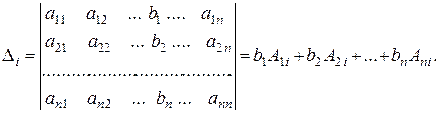
Следовательно, = 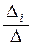. ЧТД.

Замечание. Формулы 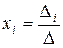дают возможность исследовать совместность СЛУ:

Если D ¹ 0, то система совместна и определенна.

Если D = 0, но хотя бы один D_i ¹ 0, то система несовместна.

Если D = 0 и все D_i = 0, то система может быть совместной, но неопределенной, а может быть и несовместной.

Пример

Доказать совместность системы линейных уравнений

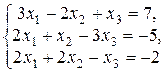
и решить её методом Крамера.

Решение. Чтобы проверить, совместна ли система, рассмотрим основную матрицу системы

А=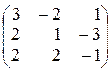

и найдем её определить

.

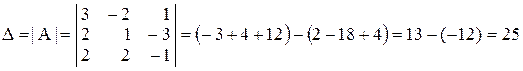Так как 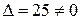, то данная система совместна и имеет единственное решение. Найдем это решение по формулам Крамера

.

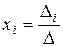Для этого вычислим вспомогательные определители , .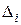

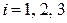Определитель D₁ получим из определителя D заменой первого столбца 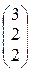столбцом свободных членов :

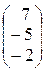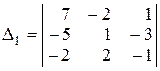= (– 7–10 –12) – (–2 – 42 –10) = –29 + 54 = 25.

Определитель D₂ получим из определителя D заменой второго столбца столбцом свободных членов:

.

И, наконец, определитель D₃ получим из определителя D заменой второго столбца столбцом свободных членов:

.

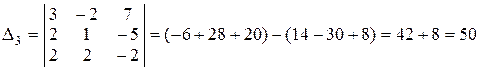Тогда получим искомое решение

, , .

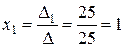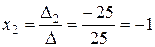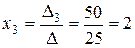Сделаем проверку:

Таким образом, найденная тройка чисел (1; –1; 2) удовлетворяет всем уравнениям заданной системы линейных уравнений и, следовательно, является решением этой системы.

Решение произвольных СЛУ

Рассмотрим СЛУ

(1)

где т ¹ п., такую систему называют «прямоугольной». В этом случае применить матричный метод или правило Крамера невозможно (определитель прямоугольной матрицы не определен). Метод решения прямоугольной системы основан на преобразовании этой системы к равносильной ей системе более простого вида.

Определение 2.

Две СЛУ называются равносильными (эквивалентными), если каждое решение одной из них является решением другой и наоборот.

Перечислим преобразования, которые можно производить над уравнениями СЛУ с целью приведения ее к равносильной системе:

· перестановка местами уравнений в системе; · умножение любого уравнения системы на число, отличное от нуля; · прибавление к обеим частям одного уравнения системы соответствующих частей другого; · отбрасывание уравнения, в котором все коэффициенты при неизвестных и свободный член равны нулю.

(6)

Один из методов решения произвольных систем, называемый методом Гаусса, состоит в том, что с помощью преобразований прямоугольная СЛУ приводится к равносильной ей системе треугольного вида

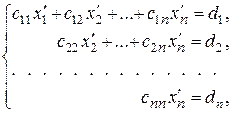(4)

или усеченного треугольного вида (трапециевидной формы)

(5)

Такие системы легко исследовать и решить. Здесь неизвестные 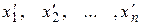– это неизвестные х_1­, х₂, ..., х_п, может быть, переставленные местами, а k £ n, k £ m .

Эти системы специального вида получают так: выбирают какое-либо уравнение и неизвестное 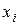в нем, поставив это уравнение и неизвестное на первое место в системе (т.е. считают 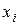= 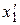), исключают выбранное неизвестное из остальных уравнений, обращая коэффициенты при этом неизвестном в ноль. Затем выбирают неизвестное 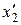, оставляют его в двух первых уравнениях на втором месте и исключают из остальных, и так далее.

Если в результате преобразований получились уравнения вида

0х_к + 0х_к+1 +...+ 0х_n = d , d ¹ 0,

то система несовместна, т.к. никакая совокупность чисел (a₁, a₂, a₃,…, a_п) этому уравнению не удовлетворяет.

Если таких уравнений в преобразованной системе нет, то полученная система (а, следовательно, и исходная) совместна.

Если получена система вида (4), то её решение находят «обратным ходом»: из последнего уравнения находят 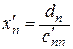, подставляя это значение в предпоследнее уравнение, находят 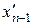, и так далее, вверх по системе, доходят до неизвестного х¢₁.

Если в результате преобразований получилась система вида (5), то поступают следующим образом.

Поскольку число уравнений системы (5) меньше числа неизвестных (k < n), то из этих уравнений можно найти только k неизвестных (коэффициенты при которых образуют отличный от нуля определитель, чаще всего это те, которые занимают первые k мест в уравнениях). Эти неизвестные называют базисными, их оставляют в левой части уравнений системы. Остальные неизвестные называют свободными, их переносят в правую часть уравнений и считают известными, принимающими произвольные значения:

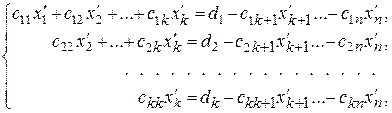
В результате получится система вида (4), из которой «обратным ходом» находят неизвестные 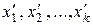как функции свободных неизвестных

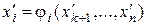
Так как свободным неизвестным можно придавать произвольные значения, то система имеет бесчисленное множество решений, а значит, и исходная система имеет бесчисленное множество решений.

Совокупность

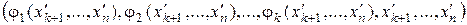
называется общим решением системы (5), и, следовательно, системы (1). Придавая в общем решении свободным неизвестным конкретные числовые значения, будем получать частное решение системы.

Реализация метода Гаусса не зависит ни от числа уравнений, ни от числа неизвестных в системе.

Рассмотрим расширенную матрицу`А исходной системы. Легко убедиться в том, что преобразования (6), приводящие систему линейных уравнений к треугольной или трапециевидной форме выполняются, по существу, над строками и столбцами этой матрицы:

§ перестановка строк;

§ умножение любой строки на число, отличное от нуля;

§ прибавление какой-либо строки матрицы, умноженной на число, к другой строке;

§ отбрасывание нулевой строки.

Поэтому вместо преобразований уравнений системы проводят соответствующие преобразования расширенной матрицы этой системы. Такие преобразования называются элементарными преобразованиями матрицы.

Рассмотрим пример. Решить систему методом Гаусса:

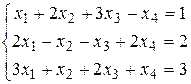
Запишем расширенную матрицу системы и произведем элементарные преобразования над строками этой матрицы:

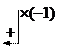
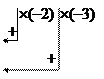
По последней матрице составим систему уравнений, равносильную исходной:

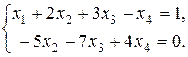
Поскольку в результате преобразований не получилось ни одного уравнения вида

0х_к + 0х_к+1 +...+ 0х_n = b , b ¹ 0,

то полученная система имеет решение. Так как неизвестных в этой системе больше чем уравнений, то разобьем эти неизвестные на базисные и свободные. За базисные возьмем два неизвестных системы, коэффициенты при которых образуют отличный от нуля определитель, это, например, х₁ и х₂ : 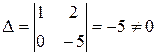. Остальные неизвестные х₃ и х₄ считаем свободными и перенесем их в правые части уравнений системы. Получим систему

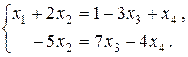
Чтобы записать все множество решений системы (общее решение), положим х₃ = с₁ , х₄ = с₂ , где с₁, с₂ – произвольные действительные числа. Получим

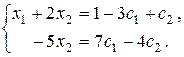
Из второго уравнения этой системы находим

.

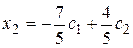Подставляя найденное значение х₂ в первое уравнение, найдем неизвестное х₁:

.

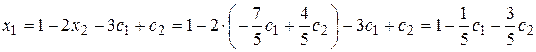Тогда можно записать

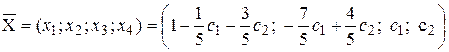, с₁, с₂ ÎR .

Эта матрица-строка и есть общеерешение заданной системы.

Придавая с₁ и с₂ любые числовые значения, можно получать частные решения:

при с₁ = 0, с₂ = 1 получим 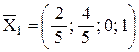– частное решение.

Другой пример. Рассмотрим систему

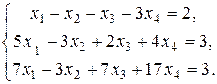
Возьмем расширенную матрицу этой системы и проведем над ней элементарные преобразования:

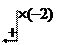
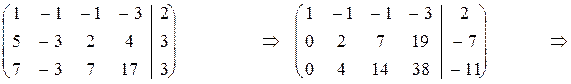
Þ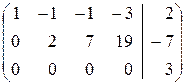

Запишем по полученной матрице систему линейных уравнений

.

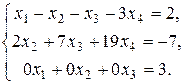Поскольку в результате преобразований получили уравнение вида

0х_к + 0х_к+1 +...+ 0х_n = b , b ¹ 0: ,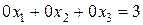

значит, исходная система решений не имеет.

Метод Гаусса является методом исследования и решения системы линейных уравнений. Во многих прикладных вопросах возникает необходимость только исследования системы. Это можно сделать с помощью понятия ранга матрицы системы и теоремы Кронекера-Капелли.

Ранг матрицы. Теорема Кронекера-Капелли.

Рассмотрим произвольную матрицу

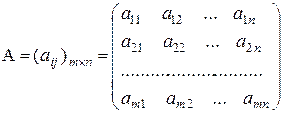
Выберем любые k строк и k столбцов этой матрицы (k £ min(m, n)) и из элементов, стоящих на пересечении выбранных строк и столбцов, составим определитель. Этот определитель называют минором k-го порядка матрицы А.

Например, для матрицы

А =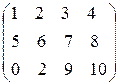

минорами второго порядка, например, являются определители: 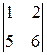, , 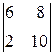а один из миноров третьего порядка имеет вид .

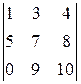Определение 3

Наивысший порядок отличных от нуля миноров матрицы А называется рангом этой матрицы.

Ранг матрицы А обозначается rangA или r(A).

Ранг матрицы обладает свойствами:

· для матрицы А = (а_ij)_m´n 0£ r(A) £ min(m, n), причем r(A) = 0 тогда и только тогда, когда А – нулевая матрица;

· для квадратной матрицы А порядка п r(A) = п тогда и только тогда, когда А – невырожденная;

· r(A) = r(A^т);

· ранг матрицы не изменится, если вычеркнуть из нее или приписать к ней нулевой ряд (т.е. строку или столбец, состоящие из одних нулей);

· ранг матрицы А_Э, полученной из матрицы А с помощью элементарных преобразований, равен рангу исходной матрицы А.

На свойствах ранга базируется следующий принцип вычисления ранга матрицы:

Заданную матрицу А элементарными преобразованиями приводят к виду

,

где c₁₁.c₂₂.c₃₃.... .c_kk ¹ 0, k £ m. Такую матрицу называют трапециевидной. Если k = m = п, то матрица А_Э – треугольная.

Так как матрица А_Э имеет отличный от нуля минор k -го порядка

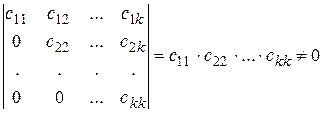
а все миноры более высоких порядков равны нулю (поскольку содержат нулевые строки), то r(А_Э) = k, а значит, и r(A) = r(А_Э) = k. Следовательно, ранг матрицы А равен числу ненулевых строк матрицы А_Э, полученной из матрицы А элементарными преобразованиями.

Справедлива следующая теорема

Теорема (Кронекера-Капелли)

Система линейных уравнений совместна тогда и только тогда, когда ранг r(A) основной матрицы системы равен рангу r( 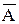) расширенной матрицы, т.е. 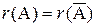(без доказательства).

Число r = 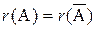называют рангом системы уравнений.

Исследование системы с помощью ранга можно проводить следующим образом:

1. Вычислить r(A) и r( 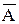); если r(A) ¹ r( 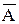), то система несовместна;

2. Если r(A) = r(`А) = r , то система совместна и

а) при r = п имеет единственное решение;

б) при r < n имеет бесчисленное множество решений. В этом случае r неизвестных СЛУ являются базисными, остальные 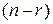неизвестных – свободными. Базисными неизвестными выбирают те, коэффициенты при которых в матрице А_Э образуют отличный от нуля минор (базисный минор).

Рассмотрим пример.

Пример

Исследовать СЛУ 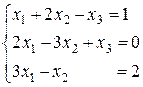и в случае совместности – решить.

Решение

Запишем расширенную матрицу системы и найдем ее ранг, преобразовав к трапециевидной форме

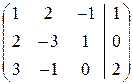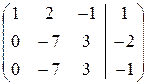`А= Þ Þ 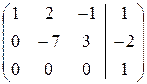= =`А_Э.

Ранг матрицы `А<sub>Э</sub> равен 3 (три ненулевые строки), а значит и r =3. Однако матрица, элементы которой стоят слева от вертикальной черты – есть матрица А<sub>Э</sub> для основной матрицы системы (которая записана в `А слева от вертикальной черты). А эта матрица имеет только две ненулевые строки, что означает r(А_Э) = r(А) = 2. Таким образом , r(A) ¹ r и в этом случае система несовместна.

Если же рассмотреть систему 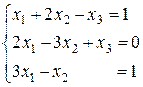, (изменен свободный член в последнем уравнении предыдущей системы), то нетрудно убедиться в ее совместности:

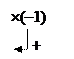
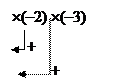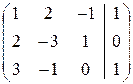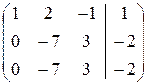`А= Þ Þ 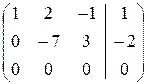= =`А_Э,

значит, r(A) = r = r = 2 – система совместна. Число неизвестных п = 3 и r < n, в этом случае система имеет множество решений.

Однородные СЛУ

Рассмотрим систему

.

Если хотя бы одно из чисел b_i, i = 1,2,…, m не равно нулю, то система называется неоднородной. Если же все b_i = 0, то система имеет вид

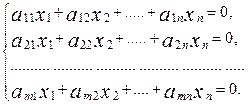(7),

и называется однородной.

Всякая однородная система совместна, так как имеет, по крайней мере, нулевое (тривиальное) решение х₁ = х₂ = …= х_п­ = 0. Следовательно, ранги основной и расширенной матрицы однородной системы равны:

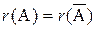=r.

Если ранг однородной системы равен числу неизвестных (r = n), то система (7) имеет единственное решение и это решение – тривиальное. Если ранг системы меньше числа неизвестных (r < n), то система имеет бесчисленное множество решений, значит, имеет нетривиальные решения. В этом случае общее решение однородной системы может быть найдено методом Гаусса.

Рассмотрим пример. Дана однородная система линейных уравнений

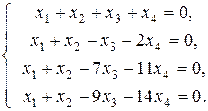
Требуется:

1) доказать, что система имеет нетривиальное решение;

2) записать общее решение этой системы уравнений и какое-либо нетривиальное частное решение.

Найдем сначала ранг системы (ранг основной матрицы), для чего преобразуем основную матрицу системы:

.

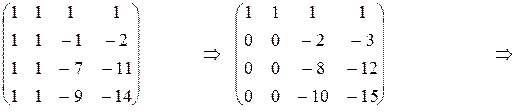
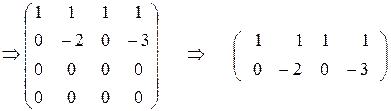Значит, r(A) = 2. Так как ранг системы меньше числа неизвестных, система имеет нетривиальные решения.

Чтобы найти общее решение системы, составим по полученной матрице систему уравнений, равносильную исходной системе. При этом учитываем тот факт, что в процессе преобразований матрицы мы поменяли местами второй и третий её столбцы, значит, в составляемой системе поменяются местами неизвестные х₂ и х₃:

.

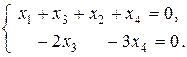Коэффициенты при неизвестных х₁ и х₃ образуют отличный от нуля определитель: , значит эти неизвестные можно взять в качестве базисных, тогда неизвестные х₂ и х₄ – свободные. Перепишем последнюю систему в виде

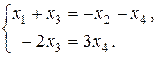(8)

Чтобы записать общее решение системы, положим х₂ = с₁ , х₄ = с₂ , где с₁, с₂ – произвольные действительные числа. Получим

.

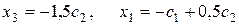Тогда общее решение однородной системы запишется в виде

где с₁ и с₂ - произвольные действительные числа.

Найдем какое-либо нетривиальное частное решение системы. Для этого придадим, постоянным 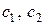произвольные значения, не равные одновременно нулю. Например, положим 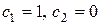, получим

.
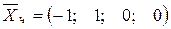