Вычисление погрешности измерения

Выясним, как будут влиять погрешности измерения отдельных величин на погрешность искомой величины. Пусть искомая величина W является функцией нескольких величин (x₁, x₂,…, x_n), измеряемых непосредственно в опыте:

W = f (x₁, x₂,…, x_n). (3)

Если бы ошибки в измерении x₁, x₂,…, x_n были бесконечно малыми, то погрешность в расчете величины W определялась бы ее полным дифференциалом:

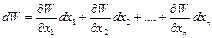. (4)

В действительности погрешности в измерениях x₁, x₂,…, x_n будут конечными величинами, поэтому максимально возможная относительная ошибка определяется как:

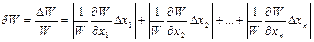. (5)

В соответствии с теорией погрешностей, принимая закон распределения погрешностей измеряемых величин нормальным, искомая величина относительной погрешности определяемой функции W = f (x₁, x₂,…, x_n) находится как среднеквадратическая

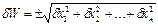, (6)

где δx₁, δx₂, …, δx_n – относительные погрешности величин x₁, x₂,…, x_n, которые измеряются при определении искомой величины W.

Пример

На экспериментальной установке (лабораторная работа № 22) методом проточного калориметрирования измеряется изобарная теплоемкость 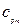воздуха.

В соответствии с выражением (1) путем измерений нужно определить подводимый тепловой поток Q_эл (Вт, Дж/с), массовый расход воздуха 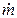и изменение его температуры Dt.

Класс точности вольтметра и амперметра известен и составляет 1,5 каждого прибора, т.е. при измерении силы тока I и напряжении U_эл на электронагревателе возможна ошибка (приведенная погрешность) 1,5 %, а погрешность определения теплового потока δQ_Эл=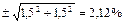

Измерение температур t₁ и t₂ осуществлялось по показаниям милливольтметра, подключенного в цепь термопар, с использованием градуировочного графика. Класс точности этого прибора неизвестен. В этом случае относительная погрешность показания милливольтметра определяется:

,

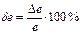где 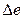- абсолютная погрешность - принимается равной половине цены деления шкалы прибора, в нашем случае с учетом чувствительности прибора составляет 5 мВ;

е - замеренные показания прибора, предположим е = 200 мВ;

тогда .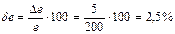

Затем по показанию милливольтметра по градуировочному графику 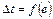определяется 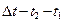. При этом допускается появление еще двух погрешностей:

по оси х ,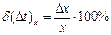

по оси y ,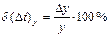

где на миллиметрованной бумаге Dx = 0,5 мм, Dy = 0,5 мм.

В данном примере на е = 200 мВ приходится х = 75 мм, а соответственно y = 57,5 мм.

Тогда , .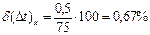

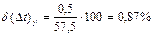Таким образом, только при измерении разности температур возможная погрешность измерения составила

.

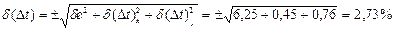Аналогично рассчитывается погрешность измерения объемного расхода:

,

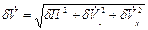где 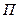- показания ротаметра.

Пусть 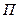=16 делениям, цена деления шкалы ротаметра 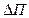=0,5, тогда 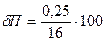=1,56%.

По градуировочному графику при 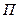=16 величина V_x = 160 мм и V_y = 84 мм, тогда 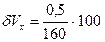= 0,31% и = 0,60%.

Таким образом погрешность определения объемного расхода будет равна 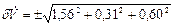=E1,70%.

Массовый расход воздуха рассчитывается по уравнению Клапейрона-Менделеева:

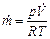, кг/с,

куда кроме объемного расхода воздуха еще входят измеряемые в опыте давление р (принимается равным барометрическому В, цена деления шкалы барометра 0,5 мм рт. ст.) и температура Т, определяемая по ртутному термометру с ценой деления 0,2 °С. Измеренные значения давления и температуры: B=755 мм.рт.ст., Т = 293 К. Тогда

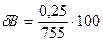= 0,033%; 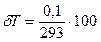=0,034%.

Следовательно, погрешность измерения массового расхода составит:

%.

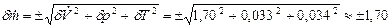Таким образом, с учетом всех ошибок при измерениях относительная среднеквадратическая погрешность определения теплоемкости составляет:

%.

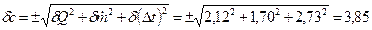Подробнее эти вопросы рассмотрены в/1/.

Лабораторная работа № 21