Завдання 5. знайти довжину дуги кривої
УКРАЇНСЬКА ДЕРЖАВНА АКАДЕМІЯ
ЗАЛІЗНИЧНОГО ТРАНСПОРТУ
Кафедра вищої математики
Інтегральне числення
Функцій однієї змінної
Виконав студент .
групи________________
_____________________
_____________________
Варіант № ___________
Перевірив____________
____________________
Харків 200
Навчальні завдання призначені для студентів загально-технічних спеціальностей. Розглянуті і рекомендовані до друку на засіданні кафедри вищої математики УкрДАЗТ, протокол № від 21 травня 2007 року .
Укладач
асист. Ю.С. Шувалова
Рецензент доцент О.О.Думіна
Загальні рекомендації
В зв'язку з невеликим обсягом аудиторних занять (лекційних і практичних) основним джерелом знань для студентів заочної форми навчання є не конспект лекцій, а підручник. Вивчення теоретичного матеріалу слід супроводжувати розв'язанням задач. Корисно для закріплення навичок, крім свого варіанта, виконати завдання ще кількох варіантів.
Дані навчальні завдання призначені для студентів загальнотехнічних спеціальностей.
Навчальні завдання призначені для виконання індивідуальних завдань, що наведені у методичних вказівках Думіна О.О., Осмаєв О.О., Шувалова Ю.С. «Інтегральне числення функцій однієї змінної та його застосування. Частини 1, 2» (далі [5]). Для успішного виконання навчальних завдань необхідно опрацювати методичні вказівки [5] в яких наведено теоретичний матеріал та приклади виконання завдань аналогічних тим, що пропонуються для самостійного розв’язання. Також для зручності в тексті навчальних завдань є посилання на формули та теореми наведені в [5]. Наприкінці наводяться умови індивідуальних завдань, та список літератури, якою можна користуватися при виконанні індивідуальних завдань.
Номери варіантів індивідуальних завдань видаються викладачем. Залік навчальних завдань згідно з учбовою програмою є необхідною умовою допуску студента до заліку або екзамену з курсу вищої математики. Навчальні завдання, що містить виконаний чужий варіант завдань, не заліковується.
Частина І
Завдання 1. Обчислити невизначений інтеграл за допомогою таблиці інтегралів:
Завдання 2. Обчислити невизначені інтеграли, зробивши заміну змінної:
а)
б)
Завдання 3. Обчислити невизначений інтеграл за допомогою формули інтегрування частинами

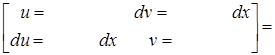
Завдання 4. Обчислити невизначені інтеграли від раціональних функцій:
а)
Підінтегральна функція є правильним/неправильним раціональним дробом
Розкладемо цей дріб на елементарні дроби з невизначеними коефіцієнтами:
Знайдемо невизначені коефіцієнти
Таким чином маємо інтеграл:
б)
Підінтегральна функція є правильним/неправильним дробом. Виділимо цілу частину цього дробу
Таким чином, ціла частина дробу дорівнює , а залишок від ділення
, тобто маємо інтеграл
Тепер підінтегральний вираз є сумою раціональної функції та правильного дробу. Спробуємо розкласти знаменник дробу на множники.
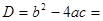
Оскільки дискримінант від’ємний, то дріб є елементарним дробом другого типу. Для його інтегрування обчислимо похідну знаменника, яку потім виділимо у чисельнику:
А також виділимо в знаменнику повний квадрат:
Таким чином, маємо три інтеграли
Розглянемо кожен інтеграл окремо, зробимо в кожному з них заміну змінної
Остаточно отримуємо:
в)
В знаменнику цієї правильної раціональної функції знаходиться двочлен у другому степені. Тому дріб розкладається на два елементарні дроби
Завдання 5. Обчислити невизначені інтеграли від тригонометричних функцій:
а)
б)
В цьому інтегралі доцільно використати універсальну тригонометричну підстановку, або можливо, якщо під знаком інтеграла є тільки комбінації функцій 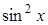 ,
, 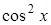 та
та 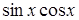 - заміну
- заміну 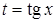
Завдання 6. Обчислити невизначені інтеграли від ірраціональних функцій:
а) Для обчислення цього інтеграла, замінимо підкорінний вираз таким чином, щоб після підстановки зникли всі корені:
б) Для обчислення інтеграла треба скористатися однією з тригонометричних або гіперболічних підстановок.
Завдання 7.
Обчислити визначені інтеграли:
a)
b)
c) За допомогою формули інтегрування частинами обчислимо інтеграл
d) За допомогою заміни змінної обчислимо інтеграл
Частина ІІ
Завдання 1. Обчислити або встановити розбіжність невласного інтеграла
Переконаємося, що даний в умові інтеграл дійсно є невласним інтегралом з необмеженими межами інтегрування (першого роду). Розглянемо підінтегральну функцію 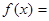 на проміжку інтегрування
на проміжку інтегрування 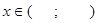 , та визначимо її особливості:
, та визначимо її особливості:
На заданому проміжку інтегрування функція 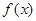 має особливості:
має особливості:
Обчислимо невизначений інтеграл окремо:
 =
=
Повертаючись до невласного інтеграла, за означенням маємо:
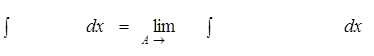
Висновок. Невласний інтеграл першого роду  збігається / розбігається.
збігається / розбігається.
Завдання 2. Обчислити або встановити розбіжність невласного інтеграла
Переконаємося, що даний в умові інтеграл дійсно є невласним інтегралом від необмеженої функції (другого роду). Розглянемо підінтегральну функцію 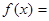 на проміжку інтегрування
на проміжку інтегрування 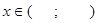 , та визначимо її особливості:
, та визначимо її особливості:
На заданому проміжку інтегрування функція 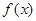 має лише одну особливість
має лише одну особливість 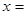
Обчислимо невизначений інтеграл окремо:
 =
=
Повертаючись до невласного інтеграла, за означенням маємо:
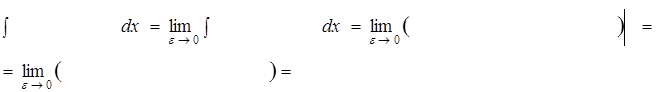
Висновок. Невласний інтеграл другого роду  збігається / розбігається.
збігається / розбігається.
Завдання 3. За допомогою ознак збіжності дослідити невласні інтеграли.
а)
Розглянемо підінтегральну функцію 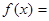 на проміжку інтегрування
на проміжку інтегрування 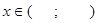 , та визначимо її особливості на цьому проміжку:
, та визначимо її особливості на цьому проміжку:
Розіб’ємо інтеграл на суму декількох інтегралів так, щоб у кожному була лише одна особлива точка. Дослідимо окремо кожен інтеграл на збіжність за допомогою ознак збіжності (см. [5] частина ІІ, теореми 1,2,3):
Висновок: невласний інтеграл  збігається / розбігається.
збігається / розбігається.
б) Розглянемо підінтегральну функцію 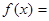 на проміжку інтегрування
на проміжку інтегрування 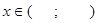 , та визначимо її особливості на цьому інтервалі:
, та визначимо її особливості на цьому інтервалі:
Дослідимо інтеграл на збіжність за допомогою ознак збіжності (см. [5] частина ІІ, теореми 1,2,3):
Висновок: невласний інтеграл  збігається / розбігається
збігається / розбігається
Завдання 3. Знайти площу фігури, обмеженої лініями
a)
Побудуємо схематично фігуру, площу якої потрібно знайти.
 По-перше, будуємо пряму
По-перше, будуємо пряму
| х | ||
| у |
По-друге, знайдемо точки перетину прямої та параболи
Отже маємо
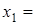 | 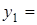 |
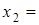 | 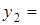 |
По-третє, будуємо параболу.
Для більш точної побудови знайдемо координати вершини параболи 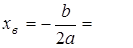 ,
, 
Оскільки коефіцієнт при 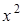 додатній/від’ємний , то вітки параболи спрямовані вверх/вниз.
додатній/від’ємний , то вітки параболи спрямовані вверх/вниз.
Схематично будуємо параболу з вершиною ( 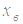 ;
; 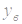 ) вітками вверх/вниз через точки перетину параболи з прямою (
) вітками вверх/вниз через точки перетину параболи з прямою ( 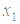 ;
; 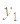 ), (
), ( 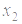 ;
; 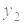 ).
).
За формулою (3) (см. [5] частина ІІ) знайдемо площу отриманої фігури
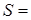
b)

Побудуємо фігуру, площу якої потрібно знайти. Знайдемо точки перетину кривих
За формулою (3) (см. [5] частина ІІ) знайдемо площу фігури
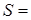
Завдання 4. Знайти довжину дуги кривої
a)
Обираємо зручну формулу (4) або (5) (см. [5] частина ІІ) для обчислення дуги кривої.
Знайдемо потрібні похідні
б)
Визначимо початкове 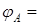 та кінцеве
та кінцеве 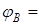 значення полярного кута.
значення полярного кута.
Обчислимо 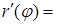
Підставляючи у формулу (6) (см [5] частина ІІ) знаходимо довжину дуги
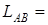
Умови індивідуальних завдань. Частина 1
Завдання 1. Обчислити невизначені інтеграли за допомогою таблиці інтегралів:
1. 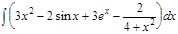 ; 2. ; 2. 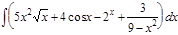 ; 3. ; 3. 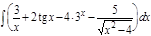 ; 4. ; 4. 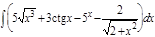 ; 5. ; 5. 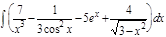 ; 6. ; 6. 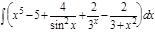 ; 7. ; 7. 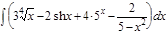 ; 8. ; 8. 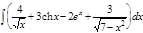 ; 9. ; 9. 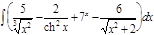 ; 10. ; 10. 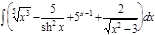 ; ; | 11. 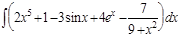 ; 12. ; 12. 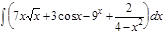 ; 13. ; 13. 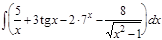 ; 14. ; 14. 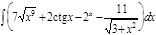 ; 15. ; 15. 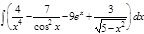 ; 16. ; 16. 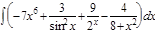 ; 17. ; 17. 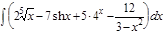 ; 18. ; 18. 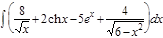 ; 19. ; 19. 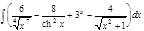 ; 20. ; 20. 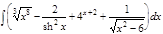 ; ; | 21. 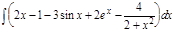 ; 22. ; 22. 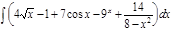 ; 23. ; 23. 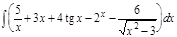 ; 24. ; 24. 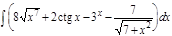 ; 25. ; 25. 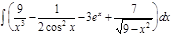 ; 26. ; 26. 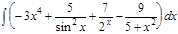 ; 27. ; 27. 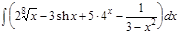 ; 28. ; 28. 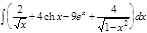 ; 29. ; 29. 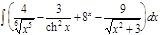 ; 30. ; 30. 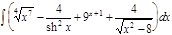 ; ; |
Завдання 2. Обчислити невизначені інтеграли, зробивши заміну змінної:
1.а) 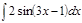 ; б) ; б) 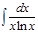 ; 2.а) ; 2.а) 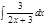 ; б) ; б) 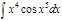 ; 3.а) ; 3.а) 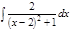 ; б) ; б) 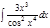 ; 4.а) ; 4.а) 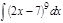 ; б) ; б) 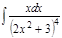 ; 5.а) ; 5.а) 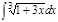 ; б) ; б) 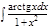 ; 6.а) ; 6.а) 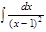 ; б) ; б) 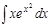 ; 7.а) ; 7.а) 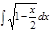 ; б) ; б) 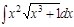 ; 8.а) ; 8.а) 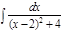 ; б) ; б) 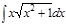 ; 9.а) ; 9.а) 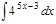 ; б) ; б) 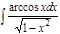 ; 10.а) ; 10.а) 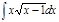 ; б) ; б) 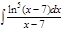 ; ; | 11.а) 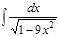 ; б) ; б) 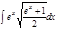 ; 12.а) ; 12.а) 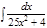 ; б) ; б) 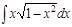 ; 13.а) ; 13.а) 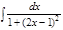 ; б) ; б) 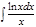 ; 14.а) ; 14.а)  ; б) ; б) 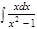 ; 15.а) ; 15.а) 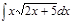 ; б) ; б) 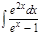 ; 16.а) ; 16.а) 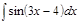 ; б) ; б) 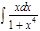 ; 17.а) ; 17.а) 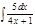 ; б) ; б) 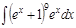 ; 18.а) ; 18.а) 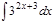 ; б) ; б) 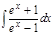 ; 19.а) ; 19.а) 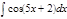 ; б) ; б) 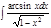 ; 20.а) ; 20.а) 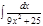 ; б) ; б) 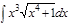 ; ; | 21.а) 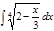 ; б) ; б) 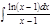 ; 22.а) ; 22.а) 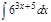 ; б) ; б) 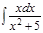 ; 23.а) ; 23.а) 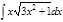 ; б) ; б) 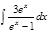 ; 34.а) ; 34.а) 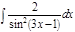 ; б) ; б) 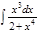 ; 25.а) ; 25.а) 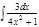 ; б) ; б) 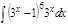 ; 26.а) ; 26.а) 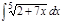 ; б) ; б) 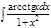 ; 27.а) ; 27.а) 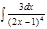 ; б) ; б) 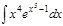 ; 28.а) ; 28.а) 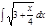 ; б) ; б) 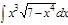 ; 29.а) ; 29.а) 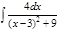 ; б) ; б) 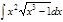 ; 30.а) ; 30.а) 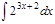 ; б) ; б) 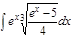 ; ; |
Завдання 3.Обчислити невизначені інтеграли за допомогою інтегрування частинами:
1. 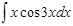 ; 2. ; 2. 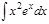 ; 3. ; 3. 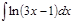 ; 4. ; 4. 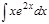 ; 5. ; 5. 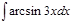 ; 6. ; 6. 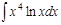 ; ; | 7 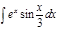 ; 8. ; 8. 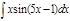 ; 9. ; 9. 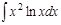 ; 10. ; 10. 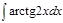 ; 11. ; 11. 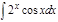 ; 12. ; 12. 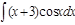 | 13. 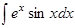 ; 14. ; 14. 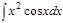 ; 15. ; 15. 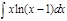 ; 16. ; 16. 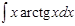 ; 17 ; 17 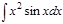 ; 18. ; 18. 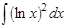 | 19. 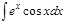 ; 20. ; 20. 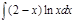 ; 21. ; 21. 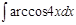 ; 22. ; 22. 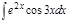 23. 23. 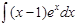 ; 24. ; 24. 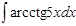 | 25. 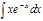 ; 26. ; 26. 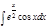 ; 27. ; 27. 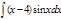 ; 28. ; 28. 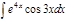 ; 29. ; 29. 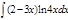 ; 30. ; 30. 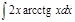 |
Завдання 4.Обчислити невизначені інтеграли від раціональних функцій:
1. а) 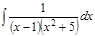 ; б) ; б) 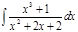 ; в) ; в) 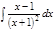 ; 2. а) ; 2. а) 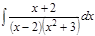 ; б) ; б) 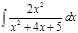 ; в) ; в) 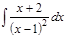 ; 3. а) ; 3. а) 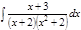 ; б) ; б) 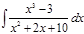 ; в) ; в) 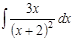 ; 4. а) ; 4. а) 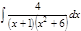 ; б) ; б) 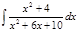 ; в) ; в) 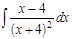 ; 5. а) ; 5. а) 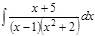 ; б) ; б) 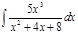 ; в) ; в) 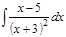 ; 6. а) ; 6. а) 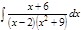 ; б) ; б) 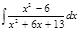 ; в) ; в) 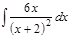 ; 7. а) ; 7. а) 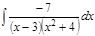 ; б) ; б) 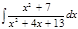 ; в) ; в) 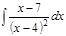 ; 8. а) ; 8. а) 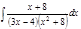 ; б) ; б) 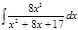 ; в) ; в) 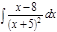 ; 9. а) ; 9. а) 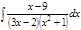 ; б) ; б) 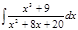 ; в) ; в) 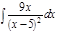 ; 10. а) ; 10. а) 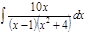 ; б) ; б) 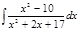 ; в) ; в) 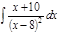 ; 11. а) ; 11. а) 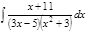 ; б) ; б) 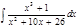 ; в) ; в) 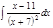 ; 12. а) ; 12. а) 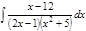 ; б) ; б) 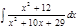 ; в) ; в) 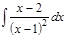 ; 13. а) ; 13. а) 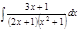 ; б) ; б) 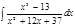 ; в) ; в) 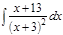 ; 14. а) ; 14. а) 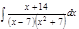 ; б) ; б) 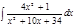 ; в) ; в) 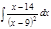 ; 15. а) ; 15. а) 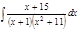 ; б) ; б) 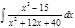 ; в) ; в) 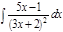 ; ; | 16. а) 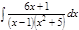 ; б) ; б) 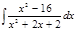 ; в) ; в) 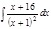 ; 17. а) ; 17. а) 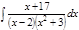 ; б) ; б) 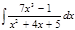 ; в) ; в) 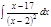 ; 18. а) ; 18. а) 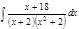 ; б) ; б) 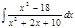 ; в) ; в) 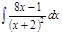 ; 19. а) ; 19. а) 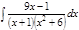 ; б) ; б) 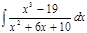 ; в) ; в) 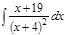 ; 20. а) ; 20. а) 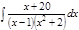 ; б) ; б) 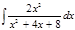 ; в) ; в) 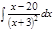 ; 21. а) ; 21. а) 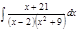 ; б) ; б) 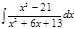 ; в) ; в) 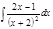 ; 22. а) ; 22. а) 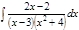 ; б) ; б) 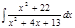 ; в) ; в) 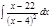 ; 23. а) ; 23. а) 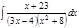 ; б) ; б) 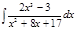 ; в) ; в) 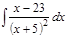 ; 24. а) ; 24. а) 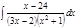 ; б) ; б) 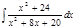 ; в) ; в) 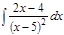 ; 25. а) ; 25. а) 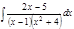 ; б) ; б) 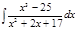 ; в) ; в) 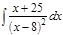 ; 26. а) ; 26. а) 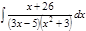 ; б) ; б) 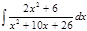 ; в) ; в) 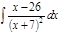 ; 27. а) ; 27. а) 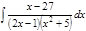 ; б) ; б) 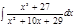 ; в) ; в) 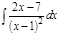 ; 28. а) ; 28. а) 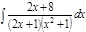 ; б) ; б) 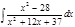 ; в) ; в) 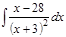 ; 29. а) ; 29. а) 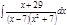 ; б) ; б) 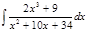 ; в) ; в) 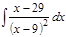 ; 30. а) ; 30. а) 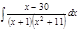 ; б) ; б) 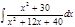 ; в) ; в) 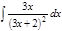 ; ; |
Завдання 5.Обчислити невизначені інтеграли від тригонометричних функцій:
1. а) 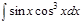 ; б) ; б) 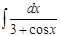 ; 2. а) ; 2. а) 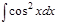 ; б) ; б) 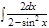 ; 3. а) ; 3. а) 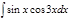 ; б) ; б) 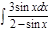 ; 4. а) ; 4. а) 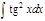 ; б) ; б) 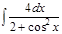 ; 5. а) ; 5. а) 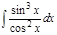 ; б) ; б) 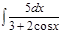 ; 6. а) ; 6. а) 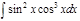 ; б) ; б) 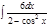 ; 7. а) ; 7. а) 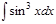 ; б) ; б) 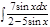 ; 8. а) ; 8. а) 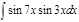 ; б) ; б) 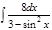 ; 9. а) ; 9. а) 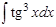 ; б) ; б) 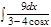 ; 10. а) ; 10. а) 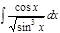 ; б) ; б) 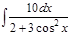 ; ; | 11. а) 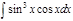 ; б) ; б) 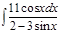 ; 12. а) ; 12. а) 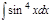 ; б) ; б) 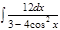 ; 13. а) ; 13. а) 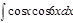 ; б) ; б) 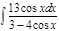 ; 14. а) ; 14. а) 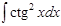 ; б) ; б) 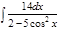 ; 15. а) ; 15. а) 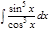 ; б) ; б) 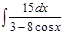 ; 16. а) ; 16. а) 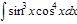 ; б) ; б) 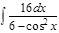 ; 17. а) ; 17. а) 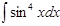 ; б) ; б) 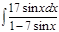 ; 18. а) ; 18. а) 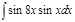 ; б) ; б) 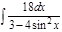 ; 19. а) ; 19. а) 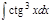 ; б) ; б) 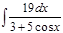 ; 20. а) ; 20. а) 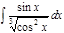 ; б) ; б) 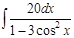 ; ; | 21. а) 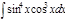 ; б) ; б) 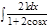 ; 22. а) ; 22. а) 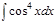 ; б) ; б) 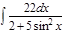 ; 23. а) ; 23. а) 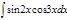 ; б) ; б) 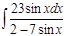 ; 24. а) ; 24. а) 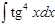 ; б) ; б) 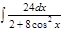 ; 25. а) ; 25. а) 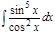 ; б) ; б) 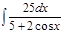 ; 26. а) ; 26. а) 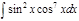 ; б) ; б) 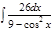 ; 27. а) ; 27. а) 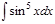 ; б) ; б) 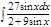 ; 28. а) ; 28. а) 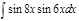 ; б) ; б) 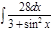 ; 29. а) ; 29. а) 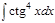 ; б) ; б) 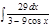 ; 30. а) ; 30. а) 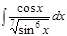 ; б) ; б) 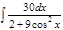 ; ; |
Завдання 6. Обчислити невизначені інтеграли від ірраціональних функцій:
1. а) 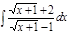 ; б) ; б) 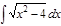 ; 2. а) ; 2. а) 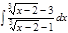 ; б) ; б) 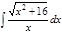 ; 3. а) ; 3. а) 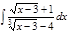 ; б) ; б) 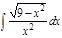 ; 4. а) ; 4. а) 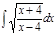 ; б) ; б) 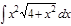 ; 5. а) ; 5. а) 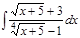 ; б) ; б) 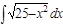 ; 6. а) ; 6. а) 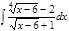 ; б) ; б) 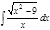 ; 7. а) ; 7. а) 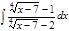 ; б) ; б) 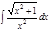 ; 8. а) ; 8. а) 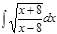 ; б) ; б) 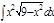 ; 9. а) ; 9. а) 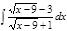 ; б) ; б) 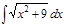 ; 10. а) ; 10. а) 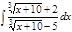 ; б) ; б) 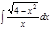 ; ; | 11. а) 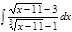 ; б) ; б) 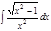 ; 12. а) ; 12. а) 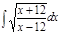 ; б) ; б) 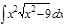 ; 13. а) ; 13. а) 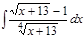 ; б) ; б) 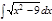 ; 14. а) ; 14. а) 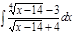 ; б) ; б) 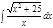 ; 15. а) ; 15. а) 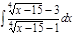 ; б) ; б) 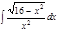 ; 16. а) ; 16. а) 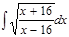 ; б) ; б) 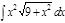 ; 17. а) ; 17. а) 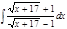 ; б) ; б) 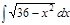 ; 18. а) ; 18. а) 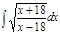 ; б) ; б) 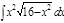 ; 19. а) ; 19. а) 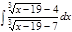 ; б) ; б) 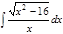 ; 20. а) ; 20. а) 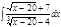 ; б) ; б) 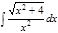 ; ; | 21. а) 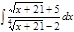 ; б) ; б) 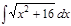 ; 22. а) ; 22. а) 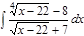 ; б) ; б) 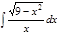 ; 23. а) ; 23. а) 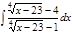 ; б) ; б) 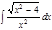 ; 24. а) ; 24. а) 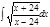 ; б) ; б) 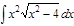 ; 25. а) ; 25. а) 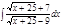 ; б) ; б) 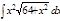 ; 26. а) ; 26. а) 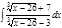 ; б) ; б) 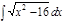 ; 27. а) ; 27. а) 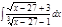 ; б) ; б) 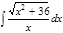 ; 28. а) ; 28. а) 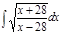 ; б) ; б) 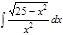 ; 29. а) ; 29. а) 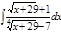 ; б) ; б) 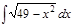 ; 30. а) ; 30. а) 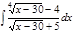 ; б) ; б) 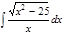 ; ; |
Завдання 7. Обчислити визначені інтеграли:
1. a) 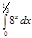 ; b) ; b) 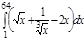 ; c) ; c) 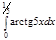 ; d) ; d) 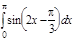 . 2. a) . 2. a) 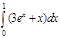 ; b) ; b) 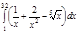 ; c) ; c) 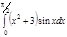 ; d) ; d) 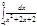 . 3. a) . 3. a) 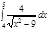 ; b) ; b) 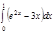 ; c) ; c) 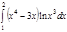 ; d) ; d) 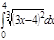 . 4.a) . 4.a) 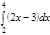 ; b) ; b) 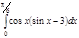 ; c) ; c) 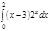 ; d) ; d) 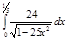 . 5.a) . 5.a) 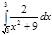 ; b) ; b) 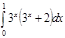 ;c) ;c) 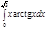 ; d) ; d) 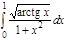 . 6. a) . 6. a) 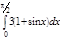 ; b) ; b) 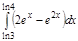 ; c) ; c) 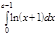 ; d) ; d) 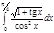 . 7.a) . 7.a) 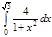 ; b) ; b) 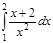 ; c) ; c) 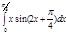 ; d) ; d) 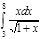 . 8.a) . 8.a) 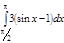 ; b) ; b) 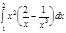 ; c) ; c) 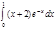 ; d) ; d) 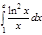 . 9.a) . 9.a) 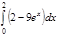 ; b) ; b) 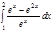 ; c) ; c) 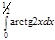 ; d) ; d) 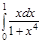 . 10.a) . 10.a) 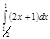 ; b) ; b) 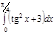 ; c) ; c) 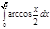 ; d) ; d) 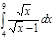 . 11.a) . 11.a) 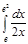 ; b) ; b) 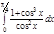 ; c) ; c) 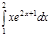 ; d) ; d) 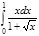 . 12. a) . 12. a) 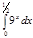 ; b) ; b) 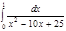 ; c) ; c) 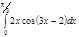 ; d) ; d) 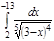 . 13.a) . 13.a) 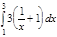 ; b) ; b) 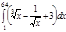 ; c) ; c) 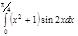 ; d) ; d) 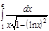 . 14. a) . 14. a) 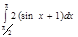 ;b) ;b) 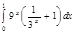 ;c) ;c) 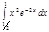 ;d) ;d) 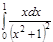 . 15. a) . 15. a) 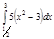 ;b) ;b) 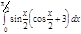 ; с) ; с) 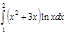 ; d) ; d) 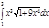 . . | 16.a) 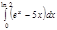 ; b) ; b) 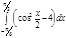 ; c) ; c) 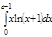 ; d) ; d) 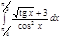 . 17.a) . 17.a) 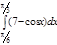 ; b) ; b) 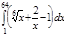 ; c) ; c) 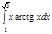 ; d) ; d) 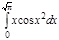 . 18.a) . 18.a) 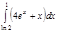 ; b) ; b) 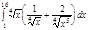 ; c) ; c) 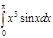 ; d) ; d) 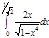 . 19.a) . 19.a) 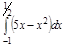 ; b) ; b) 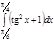 ; с) ; с) 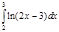 ; d) ; d) 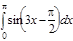 . 20.a) . 20.a) 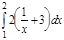 ; b) ; b) 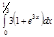 ; c) ; c) 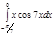 ; d) ; d) 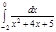 . 21.a) . 21.a) 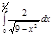 ; b) ; b) 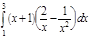 ; c) ; c) 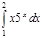 ; d) ; d) 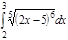 . 22.a) . 22.a) 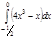 ; b) ; b) 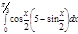 ; c) ; c) 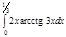 ; d) ; d) 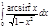 . 23.a) . 23.a) 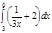 ; b) ; b) 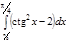 ; c) ; c) 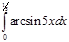 ; d) ; d) 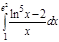 . 24.a) . 24.a) 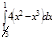 ; b) ; b) 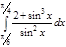 ; c) ; c) 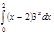 ; d) ; d) 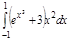 . 25.a) . 25.a) 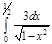 ; b) ; b) 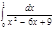 ; c) ; c) 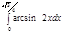 ; d) ; d) 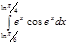 . 26.a) . 26.a) 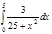 ; b) ; b) 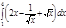 ; c) ; c) 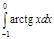 ;d) ;d) 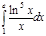 . 27. a) . 27. a) 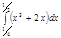 ;b) ;b) 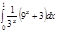 ; c) ; c) 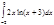 ; d) ; d) 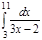 . 28.a) . 28.a) 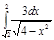 ; b) ; b) 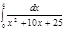 ; c) ; c) 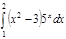 ; d) ; d) 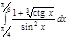 . 29.a) . 29.a) 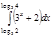 ; b) ; b) 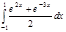 ; c) ; c) 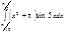 ; d) ; d) 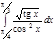 . 30.a) . 30.a) 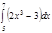 ; b) ; b) 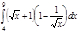 ; c) ; c) 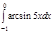 ; d) ; d) 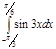 |
Частина 2.
Завдання 1. За допомогою визначення обчислити або встановити розбіжність невласних інтегралів з нескінченими межами інтегрування (першого роду):
1. 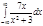 | 5. 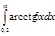 | 9. 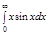 | 13. 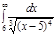 | 17. 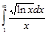 | 21. 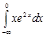 | 25. 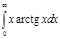 | 29. 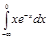 |
2. 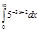 | 6. 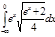 | 10. 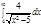 | 14. 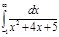 | 18. 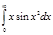 | 22. 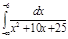 | 26. 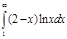 | 30. 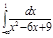 |
3. 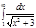 | 7. 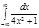 | 11. 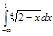 | 15. 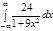 | 19. 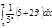 | 23. 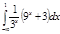 | 27. 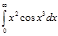 | |
4. 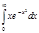 | 8. 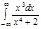 | 12. 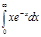 | 16. 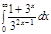 | 20. 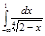 | 24. 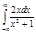 | 28. 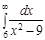 |
Завдання 2. За допомогою визначення обчислити або встановити розбіжність невласних інтегралів від необмеженої функції (другого роду):
1.  | 6. 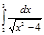 | 11. 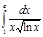 | 16. 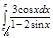 | 21. 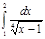 | 26. 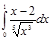 |
2. 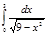 | 7. 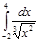 | 12. 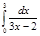 | 17. 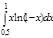 | 22. 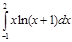 | 27. 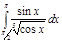 |
3. 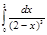 | 8. 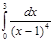 | 13. 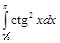 | 18. 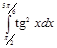 | 23. 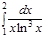 | 28. 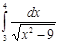 |
4. 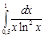 | 9. 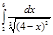 | 14. 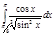 | 19. 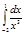 | 24. 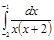 | 29. 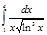 |
5. 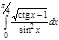 | 10. 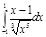 | 15. 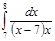 | 20. 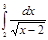 | 25. 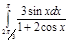 | 30. 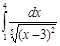 |
Завдання 3. За допомогою ознак збіжності дослідити на збіжність невласні інтеграли:
