Есептерді шығару мысалдары

1 мысал.Нүкте жиілігі n = 10 Гц гармоникалық тербеліс жасайды. Бастапқы кезде нүктенің максимал ығысуы x_max = 1 мм болды. Нүктенің тербеліс теңдеуін жазып, графигін сызыңыз.

Шешуі. Нүктенің тербеліс теңдеуін келесі түрде жазуға болады

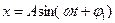(1)

немесе

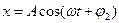(2)

мұндағы А – тербеліс амплитудасы; w - циклдік жиілік; t – уақыт; j₁ және j₂ – (1) немесе (2) жазу формаларына сәйкес келетін бастапқы фазалар.

Тербеліс амплитудасы анықтама бойынша мынаған тең

А = x_max (3)

Циклдік w жиілік пен n жиілік келесідей байланыста

w = 2pn (4)

Тербелістің бастапқы фазасы жазу формасына тәуелді. Егер (1) форманы қолдансақ, онда бастапқы фазаны t = 0 кезіндегі шартынан анықтауға болады

x_max= Аsinj₁,

осыдан

,

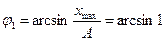немесе

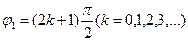
Тербеліс фазасының 2p–ге өзгеруі тербелмелі қозғалыстың күйін өзгертпейді, сондықтан

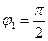(5)

Келесі формадағы жазу жағдайында

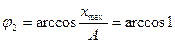
аламыз, немесе

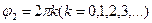
бірінші жағдайдағы сияқты келесіні анықтаймыз

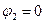(6)

(3) – (6) теңдеулерін ескерсек, тербеліс теңдеулері келесі түрге ие болады

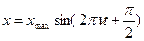
немесе

,

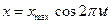мұндағы x_max = 1 мм = 10^{-3 м;} n = 10 Гц.

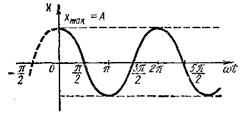
1сурет

Осы гармоникалық тербелістің графигі 1-суретте келтірілген.

2 мысал. Келесітеңдеулермен сипатталатын, бір бағыттағы екі тербеліс беттеседі

;

,

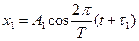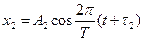мұндағы А₁ = 3 см; А₂ = 2 см; t₁ = 1/6 с; t₂ = 1/3 с; Т = 2 с.

Осы тербелістер беттесуінің векторлық диаграммасын құрыңыз, және қорытқы тербелістің теңдеуін жазыңыз.

Шешуі. Екі беттескен тербелістердің векторлық диаграммасын құру үшін, қандайда бір уақыт мезетін белгілеу керек. Әдетте, векторлық диаграмманы екі теңдеуді де канондық формаға 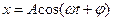келтіріп, t = 0 уақыт үшін құрады

;

.

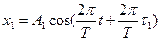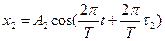Осыдан, беттесетін екі тербелістің де циклдік жиіліктері тең екендігі көрінеді

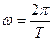. (1)

Бірінші j_1, және екінші j₂ тербелістердің бастапқы фазалары сәйкесінше тең

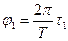(2)

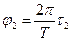(3)

(3) формулаларға мәндерін қойып, есептеулер жүргізгеннен кейін

;

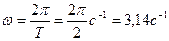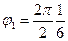рад = 30º,

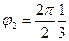рад = 60º.

2-суретт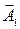е және 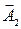векторларын сызамыз. Ол үшін А₁ = 3 см және А₂ = 2 см кесінділерін x өсіне j₁ = 30º және j₂ = 60º бұрыштарымен жүргіземіз. Қорытқы тербеліс беттесетін тербелістердің 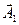және 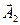амплитудаларының геометриялық қосындысына тең 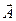амплитудамен және w жиілікпен өтеді

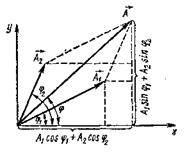
2 сурет.

= +

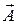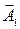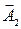
Косинустар теоремасы бойынша

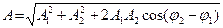(4)

Қорытқы тербелістің бастапқы фазасын векторлық диаграммадан да тікелей анықтауға болады

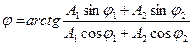(5)

(4) және (5) формулаларға мәндерін қойып, есептеулер жүргізгеннен кейін

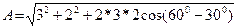см = 4,84 см.

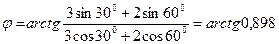= 42⁰,

немесе j = 0,735 рад.

Қорытқы тербеліс гармоникалық және жиілігі беттесетін тербелістердің жиілігіне тең болғандықтан, оны мына түрде жазуға болады

,

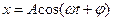мұндағы А = 4,84 см; w = 3,14 с^-1; j = 0,735 рад.

3 мысал. Жазық толқын түзу бойымен v = 20 м/с жылдамдықпен таралады. Осы түзуде, толқын көзінен x₁ = 12 м және x₂ = 15 м орналасқан екі нүкте тербеледі. Олардың фазалар айырмасы Dj = 0,75 p тең. Толқын ұзындығын l табыңыз, толқын теңдеуін жазыңыз және t = 1,2 с уақыт мезетіндегі көрсетілген нүктелердің, егер тербелістердің амплитудалары

А = 0,1 м болса, ығысуын анықтаңыз.

Шешуі. l толқын ұзындығына тең қашықтықта орналасқан нүктелер тербелістерінің фазалар айырмасы 2p-ге тең, ал бір-бірінен кезкелген Dx қашықтықта орналасқан нүктелер тербелісінің фазалар айырымы

Dj = (Dx/l)2p = ((x₂ – x₁)/l)2p.

Осы теңдікті l-ға қатысты шеше отырып келесіні анықтаймыз

l = .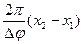

Осы теңдеуге енетін шамалардың сандық мәндерін қойып, есептегеннен кейін келесіні аламыз

l = 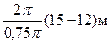= 8 м.

Жазық толқынның теңдеуін жазу үшін, w циклдік жиілікті анықтау қажет. 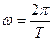(T – тербеліс периоды) және 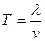болғандықтан

.

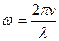Есептеулерді жүргізгеннен кейін

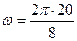с^-1 = 2p с^-1.

Тербелістің А амплитудасын, ω циклдік жиілігін және v толқынның таралу жылдамдығын біле отырып, осы жағдай үшін жазық толқынның теңдеуін жазуға болады

,

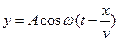мұндағы А = 0,1 м; 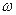= 2p с^-1; v = 20 м/с.

Көрсетілген нүктелердің y ығысуын анықтау үшін осы өрнекке t мен x-тің мәндерін қою жеткілікті

;

.

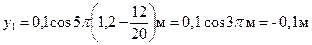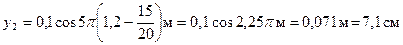4 мысал. Бұрышы аз шыны сынаға, оның қырларына перпендикуляр, толқын ұзындығы λ = 0,6 мкм параллель монохромат жарық сәулелер шоғы түседі. Осы кезде см-ге келетін пайда болған интерференциялық жолақтар саны m 10-ға тең. Сынаның α бұрышын анықтаңыз.

Шешуі. Сынаның қырларына перпендикуляр түскен сәулелер жоғарғы және төменгі қырларынан шығылады. Бұл сәулелер когерентті. Сондықтан сынаның беттерінде интерференциялық жолақтар байқалады. Сынаның бұрышы аз болғандықтан 1 және 2 шағылған сәулелер параллель болады (3 сурет).

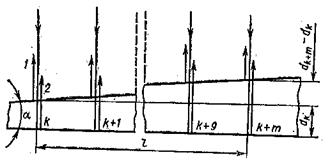Күңгірт жолақтар, сәулелердің жол айырымы жарты толқын ұзындығының жартысына тақ санынана тең сынаның бөліктерінде көрінеді

3 сурет

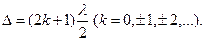(1)

Екі сәуленің 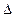жол айырымы, осы сәулелердің оптикалық жол айырымдарынан 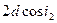және 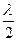толқын ұзындығының жартысынан құралады. 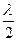шамасы 1 сәуленің оптикалық тығыз ортадан шағылған кезде пайда болтын қосымша жол айырымын көрсетеді. (1) формулаға 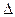жол айырымының мәнін қойып, келесіні аламыз

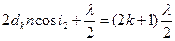(2)

мұндағы n – шынының сыну көрсеткіші (n=1,5); d_k – сынаның k номеріне сәйкес келетін күңгірт жолағы байқалған бөліктерінің қалыңдығы; i₂ – сыну бұрышы.

Түсу бұрышы нольге тең, ендеше сыну бұрышы да нольге тең болады, ал 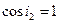. (2) теңдіктің оң жағында жақшаны ашып, ықшамдағаннан кейін

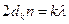(3)

k-ші номерлі күңгірт жолаққа сынаның d_k қалыңдығы, ал 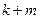-ші номерліге – d_k+m қалыңдығы сәйкес келсін. Онда 3 суреттен l қашықтықта m жолақ орналасатынын ескересек

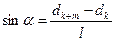(4)

(3) өрнектен d_k мен d_k+m –ны анықтайық және оларды (4) өрнекке қоямыз. Осыдан кейін, a аз бұрыш екенін ескерсек 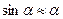, келесіні аламыз

.

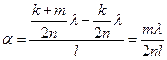Физикалық шамалардың сан мәндерін қойып, есептегеннен кейін

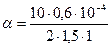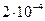рад= рад.

α –ны градуспен көрсетейік. Ол үшін радиан мен секунд арасындағы қатысты қолдануға болады: 1 рад = 206 265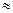^// 2,06·10^5// яғни

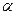= 2·­10^-4·2,06·10^5// = 41,2^//.

5 мысал. Дифракциялық тордың бетіне перпендикуляр бағытта монохромат жарық түседі. Тордың периоды d=2 мкм. Бұл тор қызыл (λ₁=0,7 мкм) және күлгін (λ₂=0,41 мкм) жарықтары үшін ең жоғары дифракциялық максимум нешінші ретті болады?

Шешуі. Дифракциялық тордың белгілі формуласының негізінде дифракциялық максимум ретінің өрнегін жазамыз

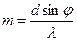, (1)

мұндағы d – тор периоды; j - дифракциялық максимум және торға түсірілген перпендикулярдың арасындағы бұрыш; l - монохромат жарықтың толқын ұзындығы. sinj 1-ден үлкен бола алмайтындықтан, бұл (1) формуладан шығады, m саны 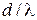-дан үлкен бола алмайды, яғни

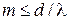(2)

(2) формулаға мәндерін қойып, келесіні аламыз

қызыл сәулелер үшін ;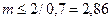

күлгін сәулелер үшін .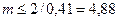

Егер максимумдар реті бүтін сан екенін ескерсек, онда қызыл түс үшін 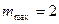және күлгін түс үшін 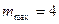болады.

6 мысал. Экранға екі S₁ және S₂ когерент жарық көздерінен сәулелер (λ=0,8 мкм түседі. Экранда интерференциялық бейне бақыланады. Сәулелердің біреуінің жолына перпендикуляр сабын қабықшасын (n=1,33) орналастырған кезде интерференциялық бейне қарама-қарсы жаққа өзгерді. Қабықшаның қандай ең минимал d_min қалыңдығында бұл жағдай орындалады?

Шешуі. Интерференциялық бейненің қарама-қарсы жаққа өзгеруі экранның интерференциялық максимум орналасқан бөліктерінде енді интерференциялық минимумдар орналасатынын білдіреді. Интерференциялық бейненің осындай ығысуы сәулелердің оптикалық жол айырымдарының тақ санға өзгеруі кезінде мүмкін болады, яғни

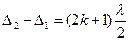(1)

мұндағы — қабықша болмаған жағдайдағы сәулелердің оптикалық жол айырымы; 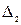— қабықша орнатылған жағдайдағы сәулелердің оптикалық жол айырымы; k=0, 1, 2, …

қабықшаның жұқа бөлігіне d_min k=0 сәйкес келеді. Осы кезде (1) мына түрге ие болады

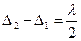(2)

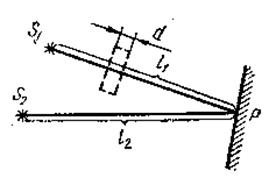
және 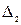оптикалық жол айырымын өрнектейік. 4-суреттен

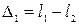(3)

4 сурет.

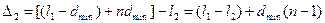(4)

және 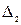өрнегін (2)-формулаға қоямыз

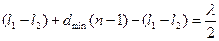(5)

немесе ,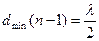

осыдан

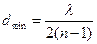
мәндерін қойып, келесіні табамыз

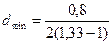мкм=1,21 мкм.

7 мысал.Табиғи жарық сәулесі сұйыққа батырылған шыны пластина бетіне түседі. Пластинадан шағылған сәуле түскен сәулемен φ=97° бұрыш жасайды (5сурет). Егер шағылған сәуле максимал поляризацияланған болса, сұйықтың сыну көрсеткішін п₁ анықтаңыз.

Шешуі. Брюстер заңы бойынша диэлектриктен шағылған жарық сәулесі, түсу бұрышының тангенсі салыстырмалы сыну көрсеткішіне сан жағынан тең болған жағдайда максимал поляризацияланған болады: 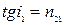, мұндағы n₂₁ —екінші ортаның (шыны) бірінші ортаға (сұйық) қатысты сыну көрсеткіші.

Салыстырмалы сыну көрсеткіші абсолют сыну көрсеткіштерінің қатынасына тең. Ендеше

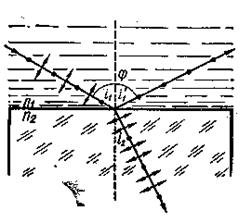
5 сурет

.

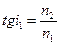Түсу бұрышы шағылу бұрышына тең болғандықтан

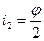және,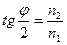

болады. Осыдан

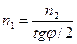
мәндерін қойып келесіні анықтаймыз

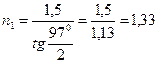
8 мысал. Екі N₁ және N₂ николь олардың жазықтықтарының арасындағы бұрыш α=60°. болатындай орналастырылған. Табиғи жарықтың интенсивтілігі I₀ неше есе кемитіндігін анықтаңыз: 1) N₁ бір никольдан өткен кезде; 2) екі никольдан өткен кезде. Никольда жарықтың жұтылу коэффициенті k =0.05. Жарықтың шағылуын ескермейміз.

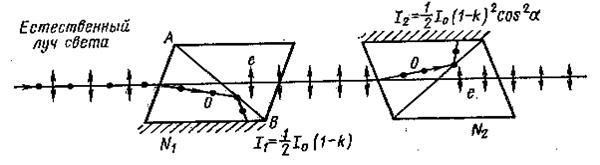
6 сурет.

Шешуі. 1. Табиғи жарық Николь призмасының қырына түсіп (6 сурет), қоссындырудың салдарынан екі сәулеге жіктеледі: қалыпты және қалыпты емес. Екі сәуле де интенсивтілік жағынан тең, және толығымен поляризацияланған. Қалыпты емес сәуленің тербелу жазықтығы сызба жазықтығында орналасқан (басты қима жазықтығы). Қалыпты сәуленің тербелу жазықтығы сызба жазықтығына перпендикуляр орналасқан. Қалыпты сәуле ОАВ шекарасынан толық ішкі шағылып, призманың күңгірт бетіне көшеді де онымен жұтылады. Қалыпты емес сәуле е өзінің интенсивтілігін кемітіп призма арқылы өтеді. Осылайша, бірінші призмадан өткен жарық интенсивтілігі

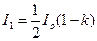
Жарықтың салыстырмалы интенсивтілігінің кемуін, бірінші никольға түскен табиғи жарықтың интенсивтілігінің I₀ поляризацияланған жарықтың интенсивтілігіне І₁ қатынасынан анықтаймыз

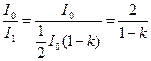(1)

(1) өрнекке мәндерін қойсақ, келесі шығады

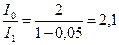
осылайша интенсивтілік 2,1 есе кемиді.

Шешуі.2. Жазық поляризацияланған интенсивтілігі І₁ жарық сәулесі N₂ екінші Никольға түседі және интенсивтіліктері тең емес екі сәулеге жіктеледі: қалыпты және қалыпты емес. Қалыпты сәуле призмамен толық жұтылады, сондықтан оның интенсивтілігін қарастырмаймыз. N₂ призмадан шыққан қалыпты емес сәуленің интенсивтілігі I₂ Малюс заңымен анықталады (екінші никольда жарықтың жұтылуын ескермегенде)

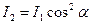
мұндағы α — поляризацияланған сәуледегі тербеліс жазықтығы мен N₂ никольдің өткізу бұрышының арасындағы бұрыш.

Екінші никольда жұтылудан интенсивтіліктің жоғалуын ескере отырып, келесіні анықтаймыз

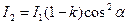
Жарықтың екі никольдан өткен кездегі интенсивтілігінің кемуін табиғи жарықтың интенсивтілігін I₀ екі никольдан өткен жарықтың интенсивтілігіне I₂ қатынасынан анықтаймыз

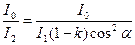
I₀/I₁ қатынасын (1) формуладағы өрнегімен алмастырсақ

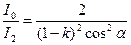
Мәндерін қойып, есептеулер

Осылайша, жарықтың екі никольдан өткеннен кейін оның интенсивтілігі 8,86 есе кемиді.

1.3. 5 – Кесте Бақылау жұмыстарының нұсқалары

Нұсқа	Есептерінің номерлері