Основы метода конечных элементов
Метод конечных элементов (МКЭ) состоит в том, что заданная система разбивается для расчета на отдельные элементы конечных размеров, объединяемых в заданную систему. Конечные элементы должны быть такой формы, которая доступна для исследования их напряженно- деформированного состояния под нагрузкой и силами взаимодействия между соседними элементами и соответствующими им перемещениями.
Элементы объединяются в заданную систему на основе условий равновесия и равенства деформаций и перемещений в местах соединения этих элементов (узлах).
Условия сопряжения элементов в узлах осуществляются на основе дополнительных допущений на стадии изучения конечных элементов.
Таким образом, в методе конечных элементов непрерывная система условно заменяется системой с конечным числом определяемых перемещений (с конечным числом степеней свободы), в которой внимание сосредоточено на анализе сил и перемещений узловых точек системы (узлов), позволяющем вести расчет не только стержневых систем, но и пластин, оболочек, объемных (массивных) тел. Следовательно, расчет таких систем сводится к решению алгебраических уравнений вместо дифференциальных.
Конечными элементами могут быть стержни или их участки в стержневых системах, элементы пластин (рис. 1) в виде треугольных и прямоугольных полей для пластин и оболочек, в виде тетраэдров и параллелепипедов для массивных тел.
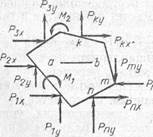 |
Рис. 1
Расчет может быть проведен по методу сил, когда за неизвестные принимаются силы взаимодействия между конечными элементами в местах их соединения, или по методу перемещений, когда за неизвестные принимаются перемещения узлов соединяемых элементов. Может быть применен и смешанный метод.
В методе сил неизвестные силы должны обеспечить равенство перемещений конечных элементов в местах их соединения (узлах), а в методе перемещений неизвестные перемещения—равновесия узлов. Однако нередко метод перемещений более удобен, чем остальные, и он в основном рассматривается далее. В расчетах по методу конечных элементов существенную роль играют матрицы податливости и матрицы жесткости. Если расчет проводится по методу сил, то применяется матрица податливости, а если по методу перемещений, то матрица жесткости.
Метод конечных элементов приложим к любым системам, в том числе и к стержневым, но все же его основное назначение — это расчет континуальных систем, пластин, оболочек и массивных тел и систем, составленных из них.
В стержневых системах, когда за неизвестные принимаются перемещения их узлов, расчет производится на основной системе метода перемещений: в этом случае метод конечных элементов представляет собой метод перемещений в особой матричной форме, без построения в основной системе исходных «единичных» эпюр, удобной для ЭВМ. Когда же в стержневых системах за неизвестные принимаются силы, расчет производится на основной системе метода сил, с особыми «узлами» системы в местах удаленных связей. В этом случае МКЭ приобретает обычную матричную форму с определением внутренних усилий в основной системе.
Если предварительное изучение конечных элементов о связи между усилиями, деформациями и перемещениями в узлах проведено точно и затем точно составлены условия сопряжения элементов, то метод будет точным. В остальных случаях, что обычно и бывает, метод приближенный. При этом, чем полнее в расчете отражены условия сопряжения элементов между собой, тем обычно метод точнее. В сложных случаях точность метода, как правило, повышается с увеличением числа конечных элементов, однако в этом случае растет число неизвестных, определение которых требует большего машинного времени для получения решений уравнений с приемлемой точностью.
Методом конечных элементов при наличии ЭВМ может быть рассчитана любая система, если выделяемые из нее конечные элементы доступны для предварительного изучения и если их число, достаточное для получения практически приемлемых результатов, не превысит при обработке возможности вычислительной машины.
