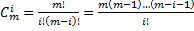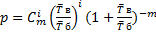Процессы гибели и размножения, финальные вероятности состояний.

Марковский процесс, протекающий в системе с конечным числом состояний в непрерывном времени называется процессом гибели и размножения, если его размеченный граф имеет вид:

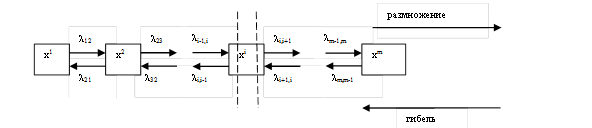
Особенность процесса проявляется также в том, что матрица плотностей вероятности является ленточной. Вероятности состояний p_i(t), определяющие эволюцию системы как систему дифференциальных уравнений Колмогорова: ;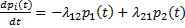

;

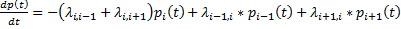
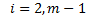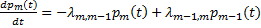
Процесс гибели и размножения как и всякий Марковский процесс имеет свойство стабилизироваться, в том смысле, что вероятности состояний стремятся к их стационарным (предельным) состояниям: 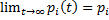. Утверждение:Если в системе с конечным множеством состояний протекают процессы гибели и размножения, то финальные вероятности состояний существуют и находятся по формулам:

.

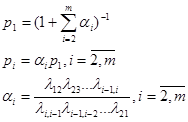Числитель – произведение наддиагональных элементов. Знаменатель - произведение поддиагональных элементов.

Финальные вероятности состояний находятся из системы у-ний, матрица которой имеет вид (пишем системы, обнуляя левые части и добавляя константы).

Матрица (коэффициентов при неизвестной) отвечает данной системе:

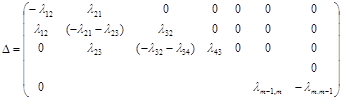II + I строки

Решаем систему методом исключения Гаусса, преобразуя матрицу с помощью эквивалентных действий.

1) Первое уравнение оставляем без изменений;

2) Ко второму уравнению добавляем первое;

3) К третьей строчке добавляю новую вторую;

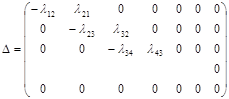
Убираем последнее уравнение и добавляем нормировочное равенство.

Записываем систему уравнений, отвечающую последней матрице:

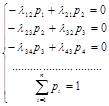
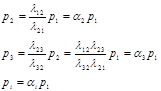
Получившееся выражение подставим в последнее нормировочное равенство: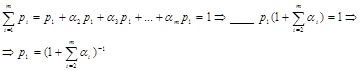

Иногда состояния системы целесообразно нумеровать не с 1 , а с 0. В этом случае расчетные формулы для вероятностей записываются в виде:

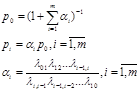
27. Процессы гибели и размножения в системе с m узлами, финальные вероятности состояний.

Имеется система с м узлами, каждый из который может выходить из строя независимо от других: на каждый узел действует пуасоновский поток отказов, событие – отказ узла. Среднее время безотказной работы узла - _б. Целесообразно рассматривать весь поток, т.к. можно говорить о его интенсивности. Отказавший узел сразу ремонтируют. На узел действует простой поток восстановлений, событие – конец ремонта. 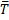Среднее время восстановления: _в. Система – совокупность м узлов, ее тек состояние определяется кол-вом работающих и ремонтирующихся узлов: х₀- 0 в ремонте, м исправно; х₁- 1 в ремонте, (м-1)-исправен. интенсивность потока отказов, действующих на один узел - λ=( 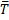_б)^-1, µ=( 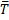_в)^-1 Финальные вер-ти могут быть найдены по общим формулам: p₀=(1+ 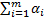)^-1, p_i=α_ip₀, α_i= 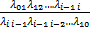. На практике финальные вер-ти удобнее выражать через _б и _в.