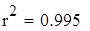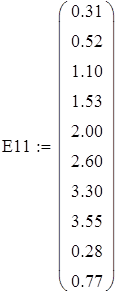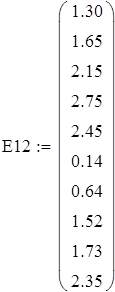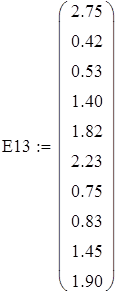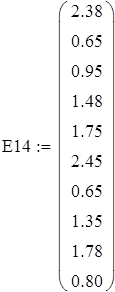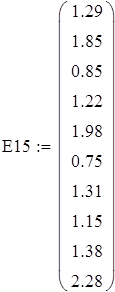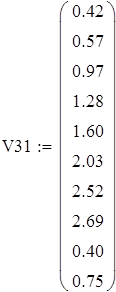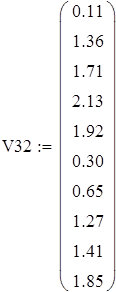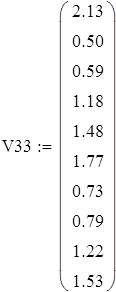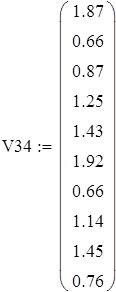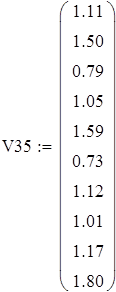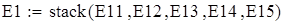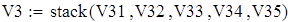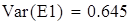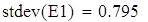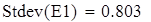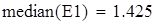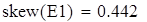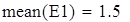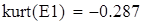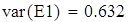СОДЕРЖАНИЕ
Введение….……………………………………………………………………..…3
Постановка задач………...…………………………………………,,…..………..4
Ход работы….……………………..………………………………………………5
Заключение……………………………………………………………………….155
Список литературы………………………………………………………………156
Введение.
Изучение основного курса математики заканчивается выполнением курсовой работы. Ее основной целью является закрепление, углубление и обобщение знаний, полученных курсантами за время обучения, и применение этих знаний к решению конкретных профессионально-направленных задач. Курсовая работа выполняется с применением пакета прикладных программ MathCad.
MathCad является математическим редактором, предназначенным как для выполнения простых арифметических расчетов, так и для реализации сложных аналитических и численных методов. В состав MathCad входят несколько взаимосвязанных систем:
- текстовый редактор для ввода, правки и форматирования текста и математических формул;
- вычислительный процессор для выполнения аналитических преобразований;
- справочная информации.
Постановка задач.
Курсовая работа ориентирована на применение математических методов обработки и анализа статистических данных, взятых из действительной отчетности о работе промысловых судов, а также работе автосервисов и радиотехнических систем и устройств. Она предполагает курсанту решение следующих задач:
- постановка проблемы и ее математическая формулировка (выбор математической модели);
- качественный анализ и аналитическое исследование выбранной математической модели с использованием современных методов и средств обработки статистических данных;
- численный анализ с помощью математических пакетов прикладных программ и современных вычислительных средств;
- оценка параметров модели и проверка ее адекватности;
- изучение взаимосвязей, существующих между основными эксплуатационными характеристиками производственных показателей работы исследуемых объектов;
- анализ полученных результатов с прогнозом возможных управленческих решений, повышающих эффективность работы производственного объекта в соответствии с обнаруженными взаимосвязями.
Ход работы.
Задача.
Статистические данные работы промысловых судов многомерны и содержат следующие показатели работы добывающих судов тралового флота в период 1990х годов.
X1-год, в котором получены данные
X2-месяц года
X3-среднесуточный вылов рыбы один судном определенного типа
X4-удельный расход топлива в тонах топлива на тонну рыбы
X5-среднесуточный расход топлива в тоннах
X6-среднее количество судов на промысле в этот период времени
X7-среднесуточный выпуск рыбной муки данным судном в тоннах
X8-среднесуточное количество замороженной рыбы в тоннах для данного типа судна
X9-год района промысла (первая цифра:1-север, 2-юг, 3-центор; вторая цифра:1-запад, 2-восток; третья цифра: 1-антлотический океан, 2-тихий океан, 3-индийский океан);
X10-среднесуточный выпуск рыбных консервов данным судном.
По своему содержанию курсовая работа предполагает:
- Формирование и описание массива экспериментальных данных конкретного варианта (какие из имеющихся в массиве данных подвергаются обработке анализу)
- Вычисление точечных статистических характеристик массива (выборочных среднего, дисперсии и среднего квадратического отклонения), асимметрии и эксцесс.
- Построение гистограмм плотности распределения и функции распределения массива экспериментальных данных.
- Построение доверительных интервалов для найденных статистических оценок с заданной доверительной вероятностью.
- Проверка гипотезы о законе распределения.
- Проверка средствами простого дисперсионного анализа гипотезы о влияние факторов «район промысла» и «месяц года» на среднесуточный вылов рыбы и удельный расход топлива для данного судна и соответствующий анализ полученных результатов с последующими выводами.
- Оценка с помощью нелинейной регрессии коэффициентов зависимости между удельным расходом топлива среднесуточного вылова рыбы в виде ln(x4) = lnc + d*ln(x3), где c и d оцениваемые коэффициенты.
- Анализ качества полученный зависимости (ее адекватности экспериментальным данным), построение доверительных границ для прогнозируемого расхода топлива и вылова рыбы, описание возможности использования полученных зависимостей в реальной практике эксплуатации судов.
- Оценка с помощью множественной регрессии неизвестных коэффициентов линейном зависимости X3=A1*X6+A2*X7+A3*X10, где A1,A2,A3 – оцениваемые коэффициенты, и анализ качества полученный зависимости.
Решение:
Статистические показатели добывающих судов
Суда типа pr333
Природа исходных данных – случайные начальные фазы, вещественные числа в диапазоне измеренные с точностью 0,01.
Ввод исходных данных.
Вводим данные порциями по 11 в отдельные массивы, которые затем объединим в массивы X3 и X7 размерности 88х1.
Объединяем полученные матрицы в один массив X3 и X7, используя функцию stack;
Расчет числовых характеристик выборок
Для Х3
| уточненная выборочная дисперсия |
| среднее квадратическое отклонение |
| уточненное среднее квадратическое отклонение |
| выборочная средняя величина |
| выборочная дисперсия входной величины |
Для Х7
| уточненная выборочная дисперсия |
| среднее квадратическое отклонение |
| уточненное среднее квадратическое отклонение |
| выборочная средняя величина |
| выборочная дисперсия входной величины |
Построение гистограммы плотности эмпирического распределения
Для Х3
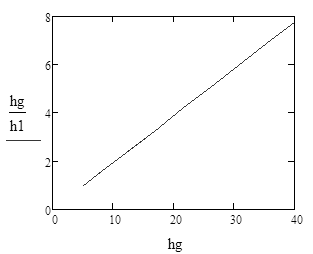
Для Х7
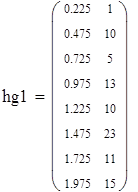
| 3. Проверка гипотезы о законе распределения для Х7 |
| Нулевая гипотеза: Н0: случайная величина распределена по закону Релея Альтернативная гипотеза: Н1: случайная величина имеет другой вид распределения. |
| Объединяем полученные матрицы в один массив Х7 |
| 4. Находим эмпирические частоты |
| 5. Для вычисления теоретических частот воспользуемся формулой ni=npi, где n - объем выборки (в нашем случае n=88), pi=f(x)dx - вероятность попадания СВ на заданный промежуток, f(x) - плотность распределения (в нашем случае Релея) |
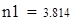
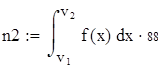
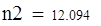
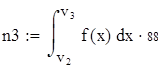
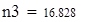
| 6. Убеждаемся, что сумма теоретических частот близка к объему выборки, равному 88. |
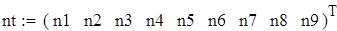
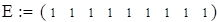
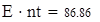
| 7. Объединяем группы теоретических частот, меньших 8. Объединяем соответствующие эмпирические частоты. |
| 8. Находим наблюдаемое и критическое значение критерия. |
| Так как наблюдаемое значение критерия больше критического (χN>χK), то нулевую гипотезу отклоняем. Следовательно, заданная выборка не подчиняется распределению Релея. |
Построение доверительных интервалов для найденных статистических оценок.
Построение доверительных интервалов для Х7
Доверительный интервал для уточненной выборочной дисперсии
| Следовательно, уточненная выборочная дисперсия Var(X7)=0.242 c вероятностью 0,95 попадает в интервал [0,082;0,268] |
| Доверительный интервал для среднего квадратического отклонения |
| Доверительный интервал для асимметрии |
| Следовательно, среднее квадратическое отклонение stdev(X7)=0.489 c вероятностью 0,95 попадает в интервал [0,208;0,51] |
| Следовательно, асимметрия skew(X7)=-0,479 c вероятностью 0,95 не попадает в интервал [-0,457;-0,256] |
| Доверительный интервал для эксцесса |
| Доверительный интервал для выборочной средней величины |
| Следовательно, эксцесс kurt(X7)=-0,643 c вероятностью 0,95 не попадает в интервал [-0,626;-0,353] |
| Следовательно, выборочная средняя величина mean(X7)=1.341 c вероятностью 0,95 не попадает в интервал [0,382;0,757] |
Задача 1.Пусть на входе линейной электрической цепи действует источник гармонического тока, задающий ток которого имеет постоянную частоту и амплитуду, но случайную начальную фазу. Результаты измерения начальных фаз тока Ф1 и тока в некоторые ветви линейной электрической цепи Ф2 измерителем разности фаз представлены выборкой. Определить числовые характеристики указанных случайных величин. Построить гистограмму плотности распределения. Показать, что эти случайные величины распределены по равномерному закону. Проверить наличие линейной связи между ними и составить уравнение регрессии.
Решение:
Природа исходных данных – случайные начальные фазы, вещественные числа в диапазоне измеренные с точностью 0,01.
Ввод исходных данных.
Вводим данные порциями по 10 в отдельные массивы, которые затем объединим в массивы Ф1 и Ф23 размерности 50х1.
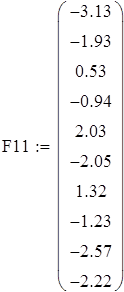
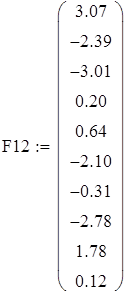
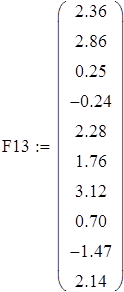
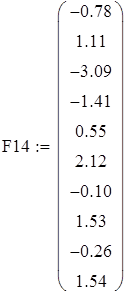
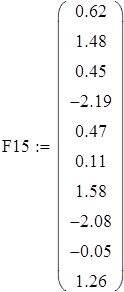
Для F1
| уточненная выборочная дисперсия |
| среднее квадратическое отклонение |
| уточненное среднее квадратическое отклонение |
| выборочная средняя величина |
| выборочная дисперсия входной величины |
Для F23
| уточненная выборочная дисперсия |
| среднее квадратическое отклонение |
| уточненное среднее квадратическое отклонение |
| выборочная средняя величина |
| выборочная дисперсия входной величины |
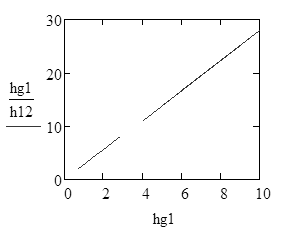
| 2. Построение гистограммы |
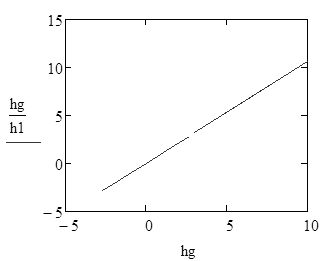
Для F23
3. Проверка гипотезы о законе распределения для 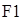 |
| Нулевая гипотеза: Н0: случайная величина распределена по равномерному закону Альтернативная гипотеза: Н1: случайная величина имеет другой вид распределения. |
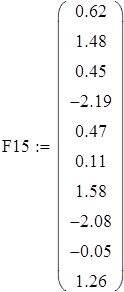
Объединяем полученные матрицы в один массив 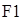 |
| 1. Расчет вероятности попадания СВ на любой из заданных интервалов и теоретические частоты |
| - значение теоретических частот на любой интервал |
| 2. Находим эмпирические частоты |
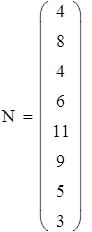
| 3. Расчет "хи-квадрат" наблюдаемого. |
| Матрица эмпирических частот |
| Матрица теоретических частот |
| Наблюдаемое значение критерия |
| 4. Расчет "хи-квадрат" критического |
| Критическое значение критерия |
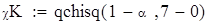
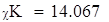
| 5. Вывод для правосторонней критической области: так как χN<χK, то нулевую гипотезу принимаем. |
| Проверка гипотезы о законе распределения для F23 |
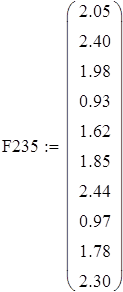
| Объединяем полученные матрицы в один массив V2о |
| 1. Расчет вероятности попадания СВ на любой из заданных интервалов и теоретические частоты |
| - значение теоретических частот на любой интервал |
| 2. Находим эмпирические частоты |
| 3. Расчет "хи-квадрат" наблюдаемого. |
| Матрица эмпирических частот |
| Матрица теоретических частот |
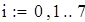
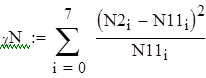
| Наблюдаемое значение критерия |
| 4. Расчет "хи-квадрат" критического |
| Критическое значение критерия |
| 5. Вывод для правосторонней критической области: так как χN>χK, то принимаем альтернативную гипотезу. |
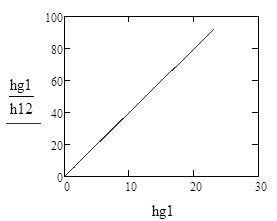
| Проверка связи между случайными величинами и составление уравнения регрессии. |
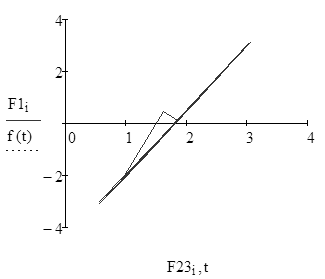
| Корреляционное поле и выбор уравнения регрессии. |
| Расчет корреляции величин F1 и F23 |
| Критическое значение критерия Стьюдента |
| Построение регрессии величин |
| Коэффициент прямой регрессии |
| Построение регрессии величин |
| Коэффициент прямой регрессии |
| Оценка статистической надежности уравнения регрессии |
| Гипотеза Но: полученное уравнение не надежно |
| Гипотеза Н1: полученное уравнение надежно |
| Расчетное значение коэффициента Фишера |
| Так как наблюдаемое значение критерия Fn больше критического Fk, то принимаем альтернативную гипотезу, следовательно, полученное уравнение регрессии является надежным, что не противоречит выводу, сделанному на основании анализа средней ошибки аппроксимации. |
Следовательно, при увеличении фактора 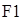 на 1%,результат F23 увеличивается на на 1%,результат F23 увеличивается на 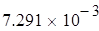 % % |
| Следовательно, 97,8% результат F23 зависит от фактора F1 а на 2,2% от случайных факторов. |
Задача 2. Пусть на входе линейной электрической цепи действует гармоническая электродвижущая сила с постоянными частотами и начальной фазой, но случайной амплитудой. Результаты измерений вольтметром амплитуды ЭДС (Е) и напряжения на одном из участков цепи (V) представлены выборкой. Определить числовые характеристики указанных случайных величин. Построить гистограмму плотности распределения. Показать, что эти случайные величины распределены по закону Релея. Проверить наличие линейной связи между ними и составить уравнение регрессии.
Решение.
1. Находим числовые характеристики указанных случайных величин.
А) Выборка E1
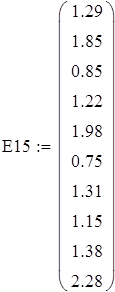
Б) Выборка V3
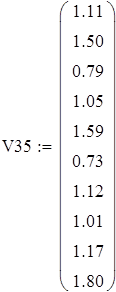
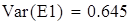
уточненная выборочная дисперсия
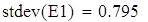
среднее квадратическое отклонение
уточненное среднее квадратическое отклонение
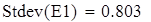

Мода не определена
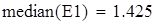
медиана
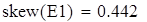
асимметрия
выборочная средняя величина
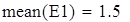
эксцесс
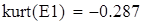
выборочная дисперсия входной величины
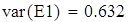
Для V3
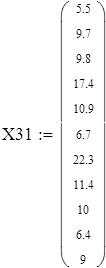
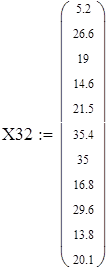
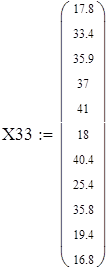
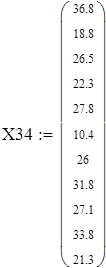
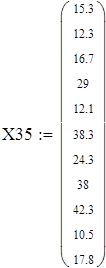
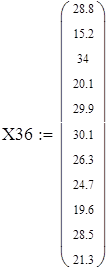
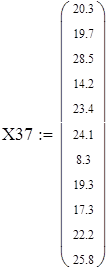
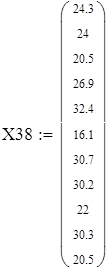
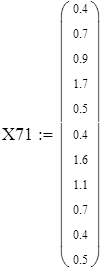
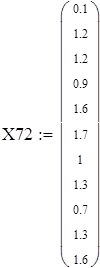
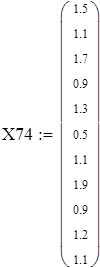
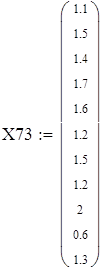
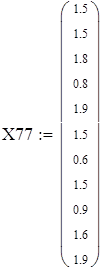
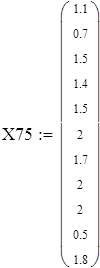
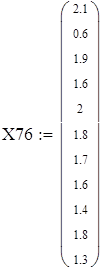
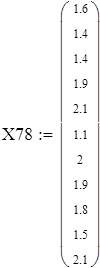
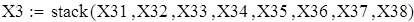
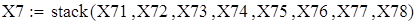
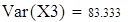
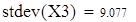
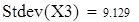

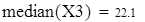
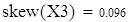
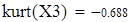
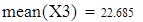
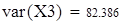
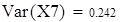
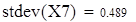
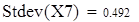
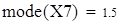
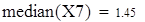
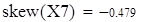
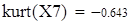
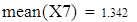
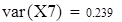
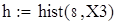
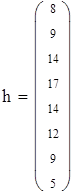
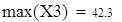
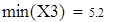
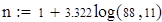
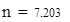
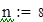
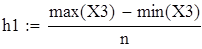
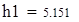
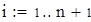
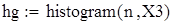
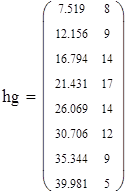

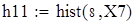
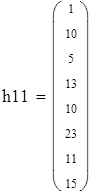
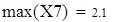
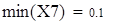
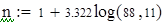
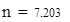
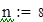
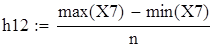
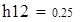
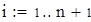
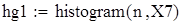
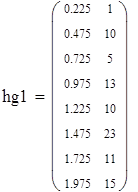

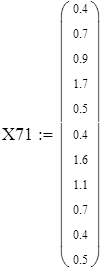
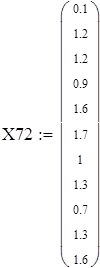
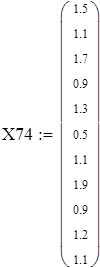
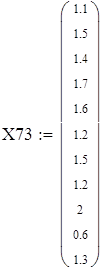
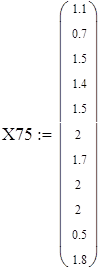
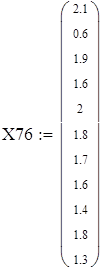
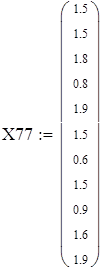
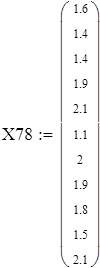
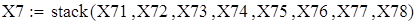
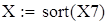
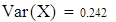
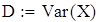
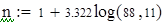
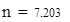
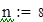
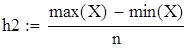
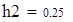

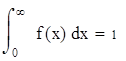
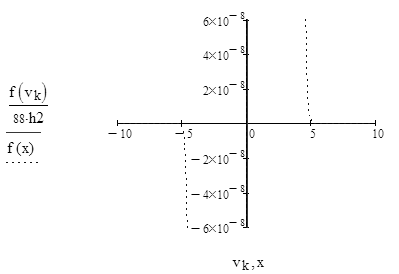
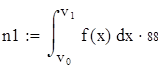
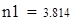
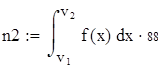
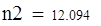
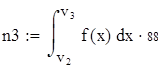
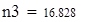
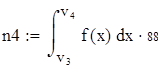
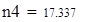
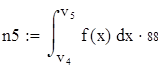
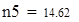
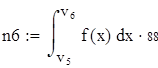
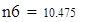
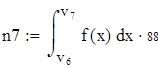
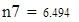
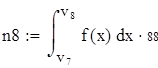
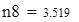
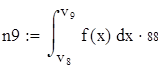
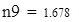
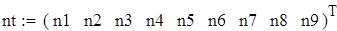
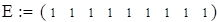
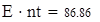
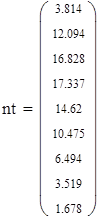
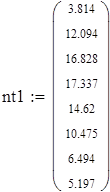
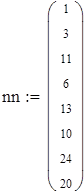
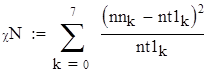
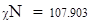
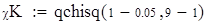
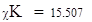
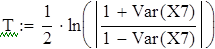
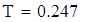
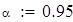
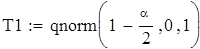
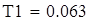
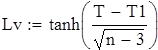
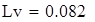
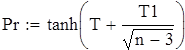
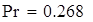
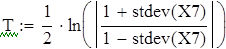
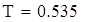
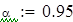
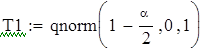
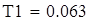
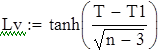
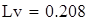
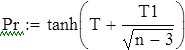
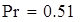
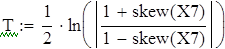
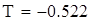
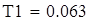
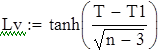
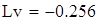
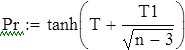
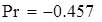
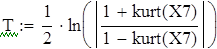
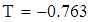
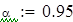
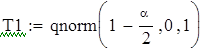
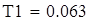
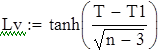
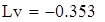
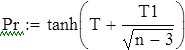
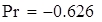
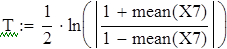
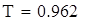
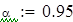
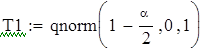
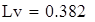
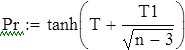
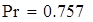
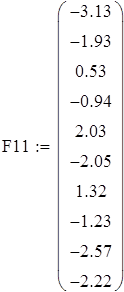
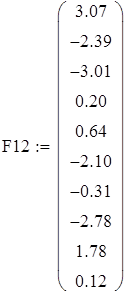
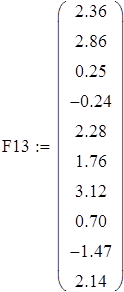
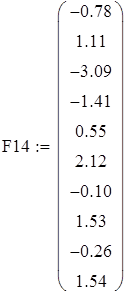
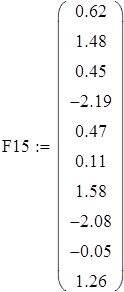
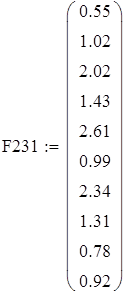
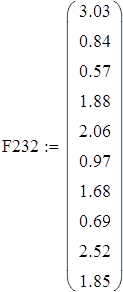
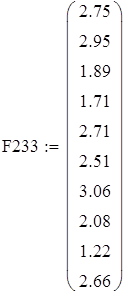
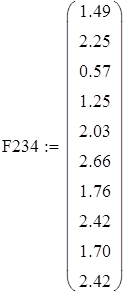
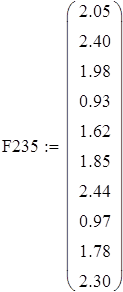
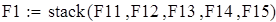
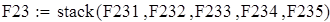
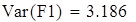
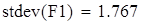
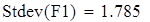

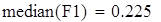
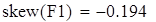
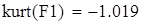
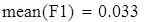
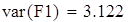
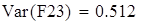
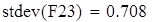
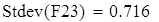
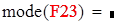
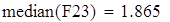
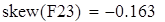
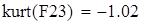
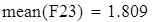
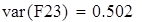
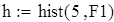
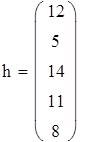
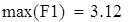
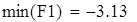
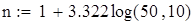
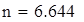
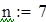
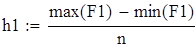
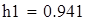
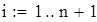
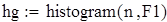
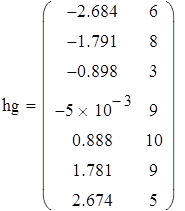


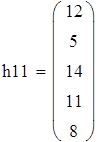
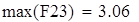
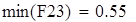
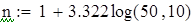
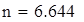
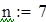
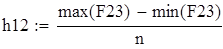
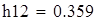
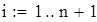
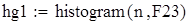
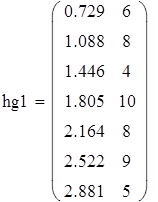
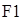
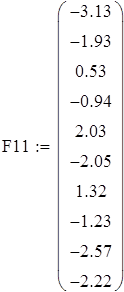
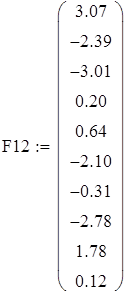
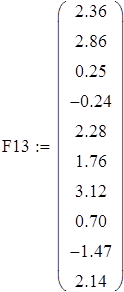
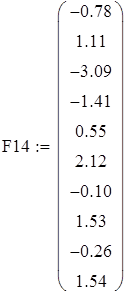
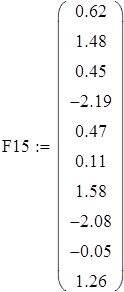
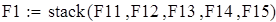
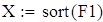
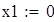
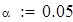
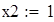
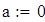
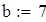
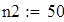
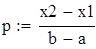
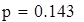
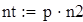
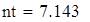
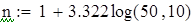
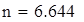
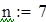
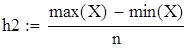
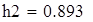
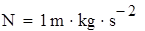
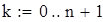
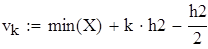

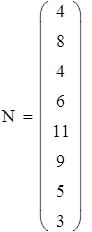
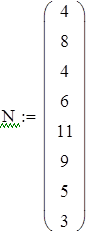
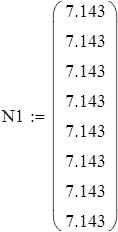
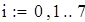
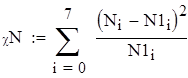
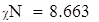
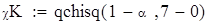
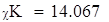
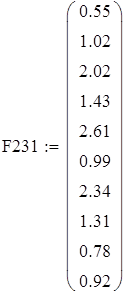
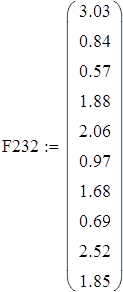
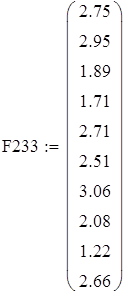
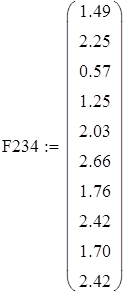
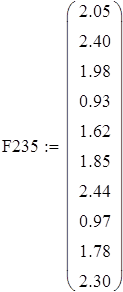
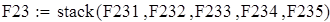
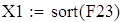
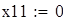
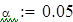
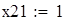
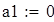
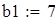
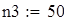
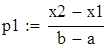
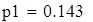
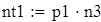
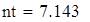
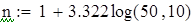
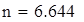
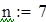
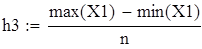
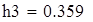
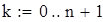
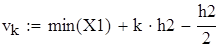
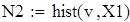
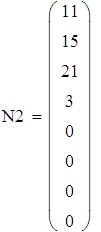
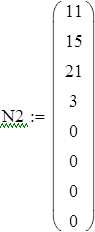
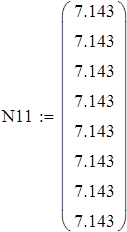
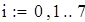
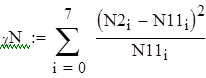
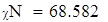
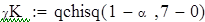
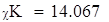
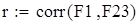
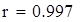
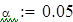
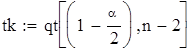
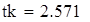
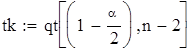
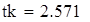
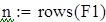
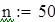
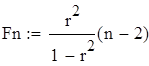
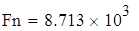
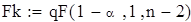
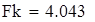
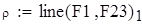
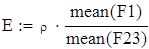
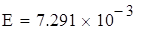
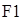 на 1%,результат F23 увеличивается на
на 1%,результат F23 увеличивается на 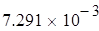 %
%