Булева алгебра. Вирази. Переведення десяткових чисел у двійкову систему

У позиційній системі числення з основою m будь-яке ціле невід’ємне число a записується послідовністю різних цифр x₁, x₂, ...,x_n, що означає

.

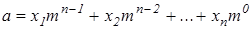Десяткова система числення використовує цифри 1, 2, 3,…, 9. У цій системі число можна записати наступним чином:

2907 = 2×10³ + 9×10² + 1×10 + 7×10⁰.

Для двійкової системи числення достатньо двох цифр 0 та 1. Послідовність цифр x₁, x₂, ..., x_n є записом двійкового n-розрядного числа 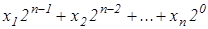. Переведення цілих десяткових чисел у двійкові здійснюється послідовним діленням вихідного числа й кожної частки від ділення на два. Одержані при цьому залишки (0 та 1) і записані у зворотному порядку дають представлення десяткового числа у двійковій системі числення.

õ Приклади задач

1. Перевести у двійкову систему числення число 26.

Розв’язок 26/2=13/2=6/2=3/2=1/2=0

26 12 6 2 0

01011

26₁₀=11010₂

Перевірка: 1×2⁴+1×2³+0×2²+1×2¹+0×2⁰=16+8+2=26.

2. Знайти порядковий номер функції f(x, y), що набуває таких значень:

f(0, 0)=1, f(0, 1)=1, f(1, 0)=0, f(1, 1)=1.

Розв¢язок.Побудуємо таблицю істинності для цієї функції.

x	y	f(x,y)

Двійковий код, що відповідає значенню цієї функції, — 1101. Переведемо двійкове число 1101₂ у десяткову систему числення

1101₂=1×2³ + 1×2² + 0×2¹ + 1×2⁰ = 8 + 4 + 0 + 1 = 13₁₀.

Таким чином, десятковий номер даної функції — 13, тобто розглянута функція імплікації f₁₃(x,y) = x ® y (див. додаток 1). Отже, функцію можна задати за допомогою двійкового коду, що відповідає її двійковому номеру.

3. Побудувати таблицю істинності для бінарної функції з порядковим номером 14.

Розв’язок

Для цього знайдемо двійкове число, яке відповідає десятковому числу 14.

14₁₀ = 1110₂.

Побудуємо шукану таблицю істинності.

x	y	f(x,y)

õ Завдання

1. Побудуйте таблиці істинності функцій та визначте їхній порядковий номер:

а) f(x, y) = (x ® y) Ù (y ® x);

б) f(x, y, z) = (x Ù y) Å (x Ù z) Å (y Ù z).

2. Перевести у двійкову систему числення числа:

а) 23; б) 64; в) 125; г) 1000.

3. Виконайте у двійковій системі наступні операції над десятковими числами:

а) 21 + 37; б) 31 + 105; в) 25 ´ 8; г) (8 + 19) ´ 11.

4. Яким десятковим числам відповідають наступні двійкові числа:

а) 1011; б) 1000110; в) 1100111; г) 110100111?

5. Скласти таблиці істинності для формул:

а) (a Ù b) ~ (a Ú b);

б) (a ~ b) = ( 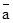Ú b);

в) .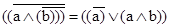

6. Яке значення істинності формули (a ~ (a 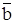Ù )) Ú 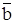, якщо висловлення а —хиба, а b — істина?

7. Записати наступні висловлювання у вигляді формул:

а) якщо Андрій погодиться чергувати у понеділок, то у вівторок піде чергувати або Віктор, або Павло;

б) якщо на перше запитання потрібно відповідати стверджувально, то на друге чи на третє запитання — заперечно;

в) перше й четверте запитання потребують однакових відповідей, а друге й третє потребують різних відповідей.

8. Запишіть формулу, що відповідає висловленню: ¢¢Для того, щоб паралелограм був квадратом, необхідно і достатньо, щоб він був ромбом та мав прямий кут або був прямокутником і мав рівні суміжні сторони¢¢.

9. Довести закон a 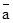~ b = Ú b.

õ Завдання для самостійної роботи

1. Спростіть за допомогою законів логіки Буля наведені нижче вирази. Потім за допомогою таблиць істинності порівняйте одержані вирази з вихідними:

а) 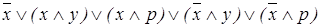x~(yÚp);

б) .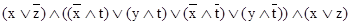

2. Розв’язати задачі обчисленням висловлювань:

а) слідчий допитав трьох осіб А, Б, С, підозрюваних у скоєнні злочину. На допиті А сказав, що показання В неправильні, В сказав, що показання С неправильні. Нарешті С сказав, що А говорить неправду і В говорить неправду. Чи може слідчий на основі цих показань установити, хто з допитаних говорить правду?

б) після батьківських зборів батько Олександра сказав класному керівнику:

- Ви не назвали мого сина серед гарних учнів, але він відмінник і до того ж найкращий лижник класу.

- Так, ви праві, але гарним учнем ми вважаємо того, хто гарно навчається, дисциплінований, допомагає відстаючим, а також бере участь у роботі наукового гуртка або займається спортом. А ваш син...

Що збирався сказати класний керівник?

3. Побудуйте таблиці істинності їх функцій та визначте їхній порядковий номер:

а) f(x, y, z) = (x Ù y) Ú (x Ù z) Ú (y Ù z);

б) f(x, y, z) = (x Ù 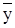) Ú (x Ù 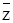) Ú (y Ù ).

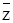Лабораторна робота № 6