Определение двойного интеграла

Вычисление площадей плоских фигур.

1.f(x)>=0 "xÎ[a,b],то _aò^bf(x)dx=S

2.S=_aò^cf(x)dx+_cò^bf(x)dx=_aò^bf(x)dx

3.S=_aò^bf2(x)-_aò^bf1(x)dx=_aò^b[f2(x)-f1(x)]dx

4.частный случай:

Y=f1(x)

Y=f2(x)

5.S=_aò^b[f2(x)+|AB|-f1(x)-|AB|]dx=_aò^b[f2(x)-f1(x)]dx

Вычисление длины дуги кривой.

Пусть дана кривая y=f(x) на [a;b], f(x)-непрерывна на [a;b].Требуется найти длину этой кривой.

Заменяем прямую вписанной ломаной.

Разобьем кривую точками на n частей. Абциссы этих точек дают разбиение Т:a=x₀<x₁<..<x_i-1<x_i<..<x_n=b

Длина отрезка [M_i-1M_i]по теореме Пифагора:∆l_i=Ö(x_i-x_i-1)²+(y_i-y_i-1)²=Ö∆x²_i-∆y²_i=Ö1+(∆y_i/∆x_i)²∆x_i

Длина всей ломаной АВ равна:

L= 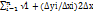_i

Для приведения l к интегральной сумме sf(f_i;x)применим х в формулу Лагранжа: ∆y=f^/(x;∆x)

∆y_i/∆x_i=f^/(x_i)=y^/(x_i)_n, x_iÎ[x_i-1;x_i]

L=s_т(f_i,x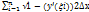_i)= _i

l-max∆x

L= 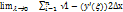_i

L=aòbÖ1+(y^/)²dx,y=y(x) или y=f(x)

Пусть плоская кривая задана параметрически уравнениями:

x=x(t),y=y(t),где tÎ[t₁,t₂]

x=x(t) x=a,t=t₁

dx=x^/(t)dt x=b,t=t₂

y^/=y^/_t/x^/_t

подставляем в формулу:

l=_aò^bÖ1+(y^/_x)dx=_aò^bÖ1+(y^/_t)²/(x^/_t)²*x^/_tdt=

=_t1ò^t2Ö((x^/_t)²+(y^/_t))/x^/_t*x^/_tdt=_t1ò^t2Ö(x^/_t)²+

+(y^/_t)²

l=_t1ò^t2Ö(x^/_t)²+(y^/_t)²dt, x=x(t)

y=y(t),tÎ[t₁,t₂]

Для кривой в пространстве:

l=_t1ò^t2Ö(x^/_t)²+(y^/_t)²dt, x=x(t)

y=y(t),tÎ[t₁,t₂]

Кривая,заданная в полярных координатах:

Формулы перехода: x=rcosj

y=rsinj

пусть кривая на плоскости описывается уравнениями,заданными в полярной системе координат:r=r(j),α£j<β

будем рассматривать такую кривую,как кривую,заданную параметрически с параметром t=j,тогда l=_αò^βÖ(x^/j)²+(y^/j)²dj

вместо x и y подставим формулы перехода: x=r(j)cosj

y=r(j)sinj

x^/_j=r^/(j)cosj-r(j)sinj

y^/_j=r^/(j)sinj+r(j)cosj

(x^/_j)²=(r^/cosj-rsinj)²=(r^/)²cos²j- 2r/cosjsinj+sin²j*r²

+ (y^/_j)²=(r^/sinj-rcosj)²=(r^/)²sin²j-2r/sinjcosj+cos²j*r²

(x^/_j)²+(y^/_j)²=(r^/)²+r²,подставляем в формулу длины:

l=_αò^βÖ(r^/)²+r²dj, r=r(j)

jÎ[α;β]

Формулы дифференциалов длины дуги кривой.

Если y=y(x),то dl=Ö1+(y^/)²dx

x=x(t)

y=y(t) ` dl=Ö(x^/_t)²+(y^/_t)²dt

x=x(t)

y=y(y)

z=z(t) dl=Ö(x^/_t)²+(y^/_t)²+(z^/_t)²dt

r=r(j), dl=Ö(r^/)²+r²dj

Вычисление объема тел.

Пусть тело ограничено с торцов плоскостями x=a и x=b и пусть известна площадь сечения тела плоскостями, перпендикулярной оси ОХ в любой точке хÎ[a;b] S(x):

1.разобъем [a;b] точками на n частей

2.на каждом отрезке ∆i разбиения выберем произвольную точку x_iÎ∆i

3.через x_i проведем плоскость x=x_i^OX и вычислим площадь сечения S(x_i)

4.на каждом отрезке ∆I заменяем тело прямым круговым цилиндром,объем которого ∆V_i=S(x_i)*∆x_i

s_т=(S, x_i)= =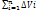

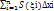
V=_aò^bS(x)dx

Частный случай:объем тела вращения,т.е. тело,образрванного вращением кривой y=y(x) a£x£b вокруг оси ОХ

S(x)=py²(x)

V=p_aò^by²(x)dx

Определение двойного интеграла.

Число I называется двойным интегралом от f(x,y) на D_i,если для любого e>0 существует такое d(e)>0,что для любого разбиения Т обл.D такого,что l<d(e),и для любой выборки x,справедливо неравенство:

|s_т(f,x)-I|<e

Обозначим: ò_Dòf(x,y)dS=ò_Dòf(x,y)dxdy=I

Кратко:I=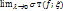

Св-ва двойного интеграла:

1.Линейности: если существует двойной интеграл от ф-ции af1(x,y)+bf2(x,y) на обл.D,то

ò_Dò(af1(x,y)+bf2(x,y))dS=aò_Dòf1(x,y)dS+bò_Dòf2(x,y)dS,где a и b-постоянные.

2.Разбиения области:если D=D1ÈD2,D1Ç=Æ,то

ò_Dòf(x,y)dS=ò_D1òf(x,y)dS+ò_D2òf(x,y)dS

3.Если "(x,y)ÎD,f1(x,y)≥f2(x,y),то

ò_Dòf1(x,y)dS≥ò_Dòf2(x,y)dS

4.| ò_Dòf(x,y)dS|£ò_Dò|f(x,y)dS

5.Теорема о среднем:если f(x,y)-определена и непрерывна в D,то существует такая точка MÎD,что

ò_Dòf(x,y)dS=f(M)S,где S-площадь D