Пример выполнения задания.

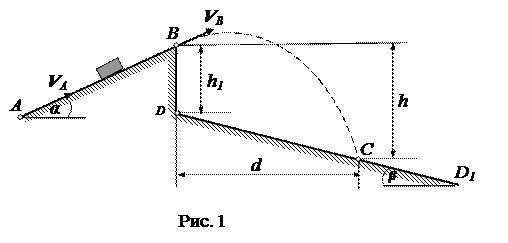Лыжник массой 60 кг подходит к точке А трамплина АВ, наклоненного к горизонту под углом α =20⁰ и имеющего длину l = 24,6 м со скоростью V_A =23,1 м/c., и от точки А до точки В дви-

жется τ секунд (рис. 1). Коэффициент трения при движении по наклонной плоскости f = 0,1.

В точке В со скоростью V_B лыжник покидает трамплин. Через Т секунд он приземляется со скоростью V_C в точке С на наклонную плоскость, которая составляет с горизонтом угол β = 40⁰ и проходитчерез точку D, расположенную на одной вертикали с точкой В на расстоянии BD = 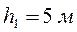. При движении в воздухе учитывать силу сопротивления, направленную против скорости и пропорциональную ее величине, коэффициент сопротивления равен k = 12.

Определить время τ движения лыжника на участке АВ и скорость в точке В.

Определить траекторию и время движения T в воздухе, построить годографы скорости и ускорения, вычислить значения скорости и ускорения точки в момент приземления.

Определить указанные параметры движения лыжника в воздухе без учета силы сопротивления.

Решение.

1. Рассмотрим движение лыжника на участке АВ. Принимаем его за материальную точку, ось Ах₁ (рис. 2) направим из начального положения лыжника вверх по наклонной плоскости (в сторону движения).

Установим начальные условия рассматриваемого движения: при t = 0, точка находилась в начале наклонной плоскости и двигалась со скоростью V_A = 18 м/c, следовательно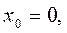

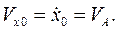
Дифференциальное уравнение прямолинейного движения записывается в виде:

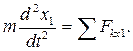
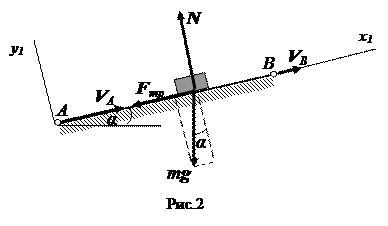
На точку действуют (рис.2): сила тяжести mg, нормальная реакция N и сила трения F_тр. Проекции этих сил на ось х₁ равны

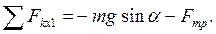Сила трения 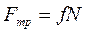, где .

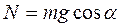Следовательно

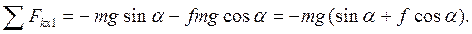
Дифференциальное уравнение принимает вид

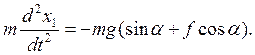
Заменим 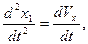и после преобразований получим

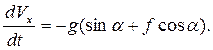
Разделим переменные и проинтегрируем

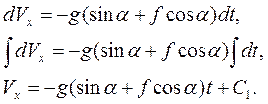
Для того, чтобы определить постоянную интегрирования С₁, подставим в последнее равенство начальные условия: t = 0, V_x0 = V_A, получаем

C₁= V_A.

Следовательно, скорость движения лыжника по трамплину в процессе движения будет равна

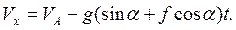(1)

Отсюда следует, что движение лыжника является равномерно замедленным с постоянным ускорением

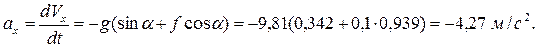
Заменим 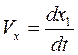, получим

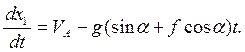
Разделим переменные и снова проинтегрируем

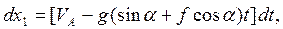
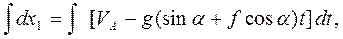
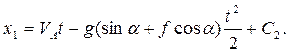
Подставим начальные условия и определим С₂: t = 0, x₀ = 0, получим С₂ = 0, значит

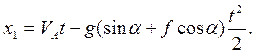(2)

По условию задачи известна длина наклонной плоскости l = 24,66 м, подставим в уравнение (2) значение х₁ = l и определим время τ, в течение которого лыжник двигался по трамплину.

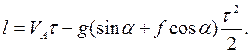
Подставим численные значения

.

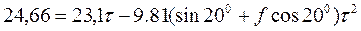После преобразований получим квадратное уравнение относительно τ

,

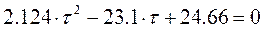откуда 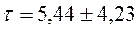, т.е.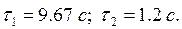

Для того, чтобы выбрать одно из полученных значений τ₁ или τ₂, определим скорость в точке В из уравнения (1)

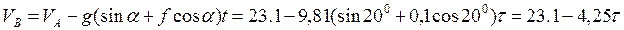Подставим в это уравнение значения τ₁ и τ₂, получим

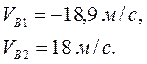
Так как скорость лыжника в точке В не может быть отрицательной, то время его движения по трамплину равно τ₂, а скорость лыжника в точке В равна

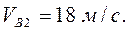
2. Рассмотрим движение лыжника в воздухе (рис.3).

Выберем начало координат в точке В, а оси координат - в направлении первоначального движения: ось х горизонтально вправо, ось у – вертикально вверх.

Составим дифференциальные уравнения движения, которое происходит под действием силы тяжести 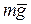, направленной вертикально вниз, и силы сопротивления 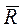, направленной противоположно скорости 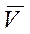. Учитывая, что сила сопротивления пропорциональна скорости, ее можно представить в виде векторного равенства: 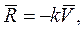где k - заданный коэффициент пропорциональности.

Дифференциальные уравнения для движения точки в вертикальной плоскости имеют вид

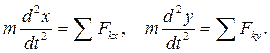(3)

Сила тяжести направлена вертикально вниз, поэтому ее проекции на оси х и у соответственно равны: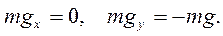

Проекции силы сопротивления 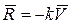на оси координат равны

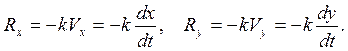
Дифференциальные уравнения (3) принимают вид

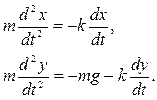(4)

Определим начальные условия.Движение в воздухе начинается со скоростью V_B, под углом α к горизонтальной прямой. Скорость в точке В определена в первой части задачи при движении по наклонной плоскости и в данном случае равна 18 м/c. Найдем проекции начальной скорости V_B на оси координат

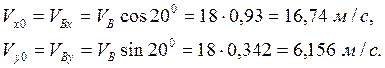
Итак, начальные условия движения лыжника в воздухе

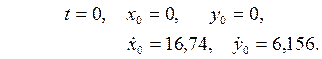
Выполним два варианта решения дифференциальных уравнений.