Нарощення по простій процентній ставці

Практичні заняття

Дисципліна «Фінанси» 1 курс

Модуль 1

1. Основні поняття фінансової математики (вищих фінансових обчислень)

Фінансова математика (або вищі фінансові обчислення) – це сукупність методів визначення вартості грошей унаслідок їхнього руху в часі. Як правило, рух грошей відбувається в процесі їх переходу від одного власника до іншого.

Процентними грішми або процентами називають суму, яку платять за користування коштами. Інакше кажучи, процентні гроші – це абсолютна величина доходу від фінансової операції.

Відзначимо суттєву відмінність фінансових і математичних процентів. Якщо у фінансах проценти - це гроші, то в математичному (і побутовому) понятті під процентами розуміють соту частину числа, що позначається символом %.

Відношення процентних грошей, отриманих за одиницю часу, до величини початкового капіталу, називається процентною ставкою або таксою. Такса виміряється в математичних процентах від величини капіталу або в частках одиниці.

Під періодом нарахування процентів розуміється відрізок часу між двома послідовними процедурами стягування процентів або термін фінансової операції, якщо проценти нараховуються один раз.

Щодо моменту часу нарахування або виплати проценти поділяються на звичайні й авансові.

Звичайні (позичкові, рекурсивні, postnumerando) проценти – це проценти, що нараховуються наприкінці періоду.

Авансові (антисипативні, дисконтні, облікові, prenumerando) проценти – це проценти, що нараховуються на початку періоду. Така форма розрахунків називається авансовою формою або обліком.

З огляду на поширеність англійських термінів, будемо приводити англійські варіанти розглянутих понять. Помітимо, що англійською процент на капітал позначається словом interest, на відміну від сотої частини числа – persent.

Розглянутим двом видам процентів відповідають і дві процентні ставки:

- звичайна ставка (рекурсивна), rate of interest;

- антисипативна (облікова, дисконтна) ставка (discount of rate).

Обидва види процентів можуть нараховуватись по двох схемах:

- схемі простих процентів, при якій проценти нараховуються тільки на початкову суму;

- схемі складних процентів, при якій проценти нараховуються як на початкову суму, так і на проценти, нараховані раніше.

На практиці для стислості застосовують терміни простих і складних процентів. Так, замість того, щоб сказати: „проценти нараховуються за схемою простих (або складних) процентів”, просто говорять: „прості (або складні) проценти”.

Звідси випливає, що як позичкові, так і авансові проценти можуть бути і простими, і складними. Цей факт ілюструє малюнок

Визначення майбутньої вартості грошей за рахунок нарахування процентів називається нарощенням грошей або компаудингом. Зворотна операція – визначення дійсної вартості майбутніх грошей називається дисконтуванням.

Останнім часом широке поширення одержали наступні позначення величин у фінансовій математиці, якими ми будемо користуватись:

PV – дійсна вартість грошей(present value);

FV – майбутня або нарощена вартість грошей (future value);

I – прості проценти;

D – авансові проценти;

i – звичайна процентна ставка;

d – дисконтна процентна ставка.

При розрахунках процентів використовується арифметична прогресія, яка відповідає схемі простих процентів, і геометрична – яка відповідає складним процентам.

ПРОСТІ ПРОЦЕНТИ

Нарощення по простій процентній ставці

Позичкові проценти

Оскільки прості проценти нараховуються тільки на початкову суму, проценти I₁, нараховані за одиницю часу, дорівнюють:

(2.1)

I₁ = PV · i

Тому нарощена вартість грошей за n періодів є

FV = PV + PV · i + … + PV ·I = PV + PV · n · I = PV (1+ ni)

тут

PV · n · i = I_n

Проценти за n періодів.

Таким чином,

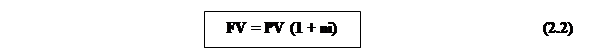
Якщо процентна ставка перемінна, а саме, протягом n₁ періодів процентна ставка дорівнює i₁, протягом n₂ періодів процентна ставка дорівнює i₂, протягом n_k періодів процентна ставка дорівнює i_r, то формула (2.2) прийме вигляд:

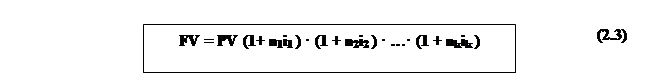Формула (2.3) – це формула для обчислення нарощеної суми грошей у випадку використання схеми простих процентів при перемінній процентній ставці.

Розрахунки з заданим числом періодів зустрічаються рідко. Частіше задається річна ставка і і термін операції, виражений у днях, рідше – у місяцях.

Позначимо термін реалізації через t (time), тривалість року, виражену в тих же одиницях, через y (year). Тоді формула (1.2) прийме вигляд:

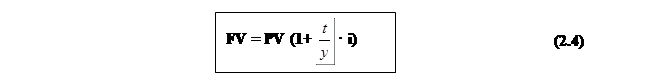де

I = 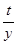·i · PV

- проценти за час t. У цьому випадку t i y можуть бути обчислені як точно, так і приблизно, відповідно до таблиці 2.1. У фінансових розрахунках, як правило, за звітний період приймається рік.

В залежності від сполучення t i y можуть бути наступні способи розрахунків.

1) Англійська практика: t i y виміряні точно. Метод називається вирахуванням точних процентів з фактичним терміном операції. Для визначення t користуються таблицею порядкових номерів днів у році: з номера дня закінчення операції віднімають день її початку, якщо день видачі і день погашення позички вважається за 1 день.

2) Французька практика: t виміряно точно, а y – приблизно. Метод називається нарахуванням звичайних (комерційних) процентів з фактичним терміном операції. У цьому випадку проценти виходять більшими, ніж у першому, тому що знаменник дробу дорівнює 360, а не 365 або 366. Звичайно по такому принципу ведуться банківські операції.

3) Німецька практика: t i y виміряні приблизно. Метод називається нарахуванням звичайних (комерційних) процентів з наближеним терміном операції. З застосовується при деяких розрахунках з населенням.

Випадок, коли t виміряно приблизно, а y – точно, на практиці не використовується.

Таблиця 2.1.

Можливі сполучення t i y.

Показник Вимір	t	y
Точний	Фактично днів у місяці	Фактично днів у році (365 або 366)
Наближений	Число днів у всіх місяцях дорівнює 30	Тривалість року дорівнює 360

Важливим поняттям фінансової математики є прибутковість фінансової операції, під якою розуміється процентна ставка за період. Формула (2.4) є вихідною для виведення базової формули ставки прибутковості фінансової операції. З (2.4) одержуємо:

(2.5)

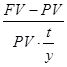
i =