Графический способ построения нелинейной регрессии
Для реализации графического метода необходимо выполнить следующие шаги:
Шаг 1: В строке главного меню необходимо выбрать Graphs ® 2D Graphs ® Line Plots (Variables…) (Графики ® Двухмерные графики ® Линейный рисунок для переменных).
Шаг 2: В появившемся окне 2D Line Plots необходимо выбрать вкладку Advanced (Расширенные) и определить переменную, на базе которой будет построен график. Для этого необходимо нажать кнопку Variables (Переменные) и в появившемся окне выбрать необходимую переменную.
Шаг 3: В поле Fit (Функции) укажем вид желаемого уравнения, в данном случае Polynomial (Парабола второй степени) и нажать ОК. Получаем график динамики ряда численности безработных в РФ и соответствующий тренд (рисунок 10.4).
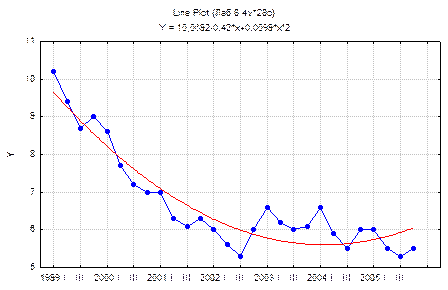
Рисунок 10.4 – Динамика численности безработных в РФ и выровненные на основе параболы второго порядка уровни
В верхней части графика выводится уравнение параболы второго порядка (рисунок 10.4). Согласно приведенным на рисунке 10.4 результатам, выбранный тип графика, довольно хорошо описывает динамику показателя.
Для сравнения результатов оценим логарифмическую прямую вида - 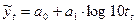 , для этого в полу Fit укажем Logarithmic и получим следующие результаты:
, для этого в полу Fit укажем Logarithmic и получим следующие результаты:
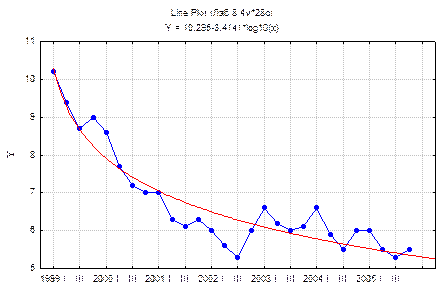
Рисунок 10.5 – Динамика численности безработных в РФ и выровненные на основе логарифмической прямой уровни
Согласно данным, приведенным на рисунке 10.5, выбранная функция (в отличие от параболы второго порядка) имеет тенденцию к снижению, что в прогнозном периоде может привести к пересечении с осью ОX. С математический точки зрения интерпретировать это случай можно как прекращение существования показателя, с социально-экономической точки зрения как полную занятость населения. Но экономическая теория утверждает, что подобного прицидента в рыночной экономике не существует. Из вышесказанного можно сделать вывод о неприемлемости подобной функции для описания динамики рассматриваемого явления.
10.5.2 Построение нелинейных трендов с помощью модуля Multiple Regression
Особенностью построения нелинейных моделей на основе временных данных (в отличие от пространственных данных) является то, что в качестве независимой переменной в данном случае будет выступать момент времени t. В остальном все действия аналогичны описанным в главе 5:
Шаг 1. Вводим в рассмотрение переменную t, при этом t=0 в 4 квартале 1998 года. Далее преобразуем данную переменную, а имен вводим следующие переменные:
- t2 – для этого после переменной t образуем новый столбец t^2 и в поле Long name (label or formula with Functions): вводим =v2^2;
-  - после столбца t^2 добавляем переменную 1/t и указываем=1/v2;
- после столбца t^2 добавляем переменную 1/t и указываем=1/v2;
- log10t – после столбца 1/t добавляем переменную log10 t и указываем =log10(v2)
Шаг 2.В главном меню выбираем Statistics ® Multiple Regression, для построения параболы второго порядка в качестве зависимой переменной укажем Y, не зависимых – t и t^2.
Для оценки гиперболы необходимо в поле Dependent var. указать Y, а в поле Impendent var. - 1/t .
Для оценки логарифмической функции необходимо в поле Dependent var. указать Y, в поле Impendent var. - log10t.
Результаты оценки трех кривых приведем в таблице 10.3.
Таблица 10.3 - Сравнительные характеристики динамических моделей ряда численности безработных в РФ
| Модель | Парабола второго порядка | Гипербола | Логарифмическая прямая |
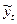 = 10,06 -0,42tt+0,01t2t (34,15) (-8,96) (6,30) = 10,06 -0,42tt+0,01t2t (34,15) (-8,96) (6,30) | 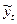 =5,91 + 5,66 =5,91 + 5,66 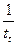 (34,76) (7,98) (34,76) (7,98) | 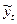 =10,295-3,41 log10tt (38,72) (-14,29) =10,295-3,41 log10tt (38,72) (-14,29) | |
| Коэффициент детерминации R2 | 0,878 | 0,71 | 0,887 |
| Скорректированный коэффициент детерминации AR2 | 0,868 | 0,699 | 0,883 |
| F-критерии Фишера | 89,615 | 63,748 | 204,159 |
| Стандартное отклонение | 0,483 | 0,729 | 0,455 |
В результате построения моделей было получено, что наилучший коэффициент детерминации наблюдается у логарифмической прямой и равняется 0,89, т.е. 89% колебаний изучаемого показателя описывается данной моделью.
Корректную оценку адекватности построенной модели дает скорректированный коэффициент детерминации, так как он показывает такую оценку тесноты связи, которая не зависит от числа факторов в модели и потому может сравниваться по разным моделям с разным числом факторов. В данном случае наибольшее значение так же получено у логарифмической модели.
Значение F-критерий Фишера у всех трех моделей получены довольно большими, т.е. подтверждается статистическая значимость оцененных уравнений регрессии.
Так как полученные модели являются статистически значимыми переходим к прогнозированию уровней ряда на 2006 год. При этом по причинам описанным выше логарифмическая прямая будет исключена из рассмотрения. Поэтому для прогнозирования используем параболу второго порядка и гиперболу.
Шаг 3. Для прогнозирования неизвестных уровней по параболе необходимо в окне Multiple Regression Results выбрать вкладку Residuals/assumptions/prediction (Отклонения/распределения/предсказания) и воспользоваться кнопкой Predict dependent variable (Прогнозирование зависимой переменной).
В появившемся окне в окно Specify values for indep. vars (Определение неизвестных значений для зависимой переменной) последовательно укажем значения (результаты расчета представим в таблице 10.4):
| t | t^2 |
Шаг 4. Для прогнозирования неизвестных уровней по гиперболе необходимо после оценки соответствующей модели в окне Specify values for indep. Vars последовательно указать результаты расчета представим в таблице 5):
| 1/t |
| 0,034 |
| 0,033 |
| 0,032 |
| 0,031 |
Таблица 10.4 – Прогнозируемые значения числа безработных в РФ
| Годы | Фактические значения | Прогнозные значения по параболе второго порядка | Нижняя дов. граница -95,0% | Верхняя дов. граница +95,0% | Прогнозные значения по гиперболе | Нижняя дов. граница -95,0% | Верхняя дов. граница +95,0% |
| 2006 I | 5,8 | 6,195 | 5,587 | 6,802 | 6,099 | 5,776 | 6,422 |
| II | 5,6 | 6,357 | 5,661 | 7,054 | 6,093 | 5,770 | 6,417 |
| III | 5,4 | 6,540 | 5,746 | 7,333 | 6,088 | 5,763 | 6,412 |
| IV | - | 6,742 | 5,843 | 7,640 | 6,082 | 5,757 | 6,407 |
Согласно полученным прогнозным значениям на основе параболы второго порядка, имеем рост показателя в 2006 году, при этом относительно фактических данных прогнозные значения завышены.
Прогнозы, полученные на основе гиперболы, имеют тенденцию к снижению, т.е. они более адекватно описывают фактические данные (с 1-3 квартал 2006 года наблюдается снижение числа безработных). В пользу гиперболы говорит и тот факт, что прогнозные уровни на k периодов будут стремиться к значению 5,91 (согласно свойствам гиперболы), но не пересекут это значение.
Подводя итоги проведенного анализа ряда численности безработных можно сделать вывод о том, что наилучшей моделью описывающих тенденцию показателя является гипербола, т.к. параметры модели получены статистически значимыми и прогнозы в большей степени соответствуют фактическим значениям.
Тесты для самоконтроля
1) Если в при расчете параметров параболы второго порядка получаем, что а1 < 0 и а2 > 0, то:
а) кривая симметрична относительно высшей точки
б) кривая симметрична относительно низшей точки
в) имеем медленно повышающуюся функцию с верхней асимптотой
2) Если в при расчете параметров параболы второго порядка получаем, что а1 > 0 и а2 < 0, то:
а) кривая симметрична относительно высшей точки
б) кривая симметрична относительно низшей точки
в) имеем медленно повышающуюся функцию с верхней асимптотой
3) Какое уравнение соответствует следующей системе нормальных уравнений, применяемой для определения параметров уравнения (по методу наименьших квадратов)
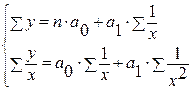
а) 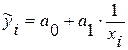
б) 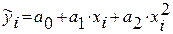
в) 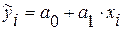
4) Какое уравнение соответствует следующей системе нормальных уравнений, применяемой для определения параметров уравнения (по методу наименьших квадратов)
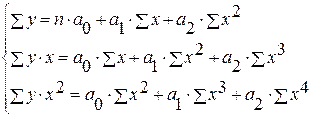
а) 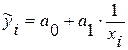
б) 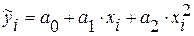
в) 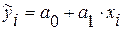
5) Приведенная модель 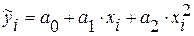 является:
является:
а) параболой второго порядка
б) гиперболой
а) параболой первого порядка
6) Приведенная модель 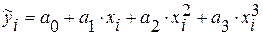 является:
является:
а) параболой второго порядка
б) параболой третьего порядка
а) параболой первого порядка
7) Приведенная модель 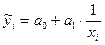 является:
является:
а) параболой второго порядка
б) равносторонней гиперболой
а) параболой первого порядка
