Структурный анализ механизма
Филиал в г. Северодвинске Архангельской области
| Кафедра проектирования подъемно-транспортного и технологического оборудования | ||||||||||||||||
| (наименование кафедры) | ||||||||||||||||
| Дрокина Елена Владиславовна | ||||||||||||||||
| (фамилия, имя, отчество студента) | ||||||||||||||||
| Институт | Севмашвтуз | курс | группа | |||||||||||||
| Конструкторско-технологическое обеспечение машиностроительных производств | ||||||||||||||||
| (код и наименование направления подготовки/специальность) | ||||||||||||||||
| РАСЧЁТНО-ГРАФИЧЕСКАЯ РАБОТА | ||||||||||||||||
| По дисциплине | Теория машин и механизмов | |||||||||||||||
| На тему | Анализ исполнительного механизма станка для нарезания конических зубчатых колёс | |||||||||||||||
| (наименование темы) | ||||||||||||||||
| (номер и наименование программы подготовки) | ||||||||||||||||
| Отметка о зачёте | ||||||||||||||||
| (дата) | ||||||||||||||||
| Руководитель | к.т.н. доцент | Д.В. Кузьминн | ||||||||||||||
| (должность) | (подпись) | (инициалы, фамилия) | ||||||||||||||
| (дата) | ||||||||||||||||
| Северодвинск 2016 | ||||||||||||||||
ЛИСТ ДЛЯ ЗАМЕЧАНИЙ
ОПИСАНИЕ РАБОТЫ МЕХАНИЗМА ПО КИНЕМАТИЧЕСКОЙ СХЕМЕ
На рисунке 1 изображен механизм станка для нарезания конических зубчатых колёс.
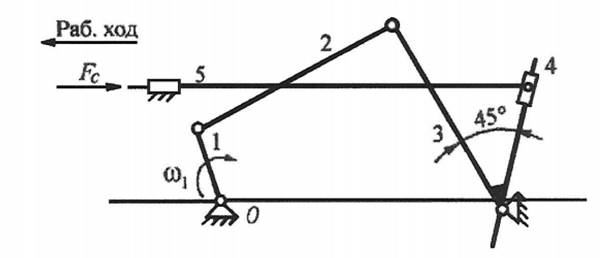
Рисунок 1 – Механизм станка для нарезания конических зубчатых колёс.
Механизм станка для нарезания конических зубчатых колёс состоит из шести звеньев:
0. Стойка.
1. Кривошип.
2. Шатун.
3. Кулиса.
4. Кулисный камень.
5. Суппорт.
Механическая энергия привода станка подводится к входному звену – кривошипу 1,который совершает вращательное движение. Шатун 2 совершает плоскопараллельное движение передавая вращательное движение с кривошипа 1 на кулису 3. Кулиса 3 совершает возвратно-качательноедвижение передавая сложное движение на кулисный камень 4.
1)Возвратно-качательное-вместе с кулисой.
2)Возвратно-поступательное - вдоль кулисы.
Кулисный камень 4 сообщает возвратно-поступательное движение суппорту 5. Суппорт 5 выполняет рабочий ход слева направо и холостой в обратном направлении.
СТРУКТУРНЫЙ АНАЛИЗ МЕХАНИЗМА
Рассмотрим исполнительный механизм станка, изображённого на рисунке 1.
Данный механизм состоит из шести звеньев:
0. Стойка.
1. Кривошип.
2. Шатун.
3. Кулиса.
4. Кулисный камень.
5. Суппорт.
Звенья механизма образуют семь кинематических пар:
0 – 1, 1 – 2, 2 – 3, 0 – 3, 4 – 5 – вращательные, одноподвижные, пятого класса;
3 – 4, 5 – 0 – поступательные, одноподвижные, пятого класса.
Указанные кинематические пары – низшие; следовательно, рассматриваемый механизм является рычажным. Звенья механизма движутся в плоскостях, параллельных неподвижной плоскости – исследуемый механизм является плоским. Он не содержит звеньев. Образующих только одну кинематическую пару; следовательно является замкнутым. Звенья механизма образуют два замкнутых контура:
1. 0 – 1 – 2 – 3 – 0.
2. 0 – 3 – 4 – 5 – 0.
Число степеней свободы механизма определим, применяя универсальную структурную формулу Чебышева:
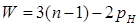
Где n –число звеньев механизма;
Рн – число низших кинематических пар;
Рв – число высших кинематических пар;
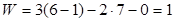
Таким образом механизм обладает одной степенью свободы.
Выявим избыточные связи: связи типа А и Б в данном механизме отсутствуют. Число избыточны связей, образованных при замыкании контуров (тип В) определим из формулы Малышева:
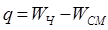
где WЧ – число степеней свободы, найденное по формуле Чебышева, WСМ – число степеней свободы, найденное по формуле Сомова – Малышева:
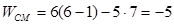
Таким образом число избыточных связей типа В будет равно :
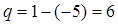
В соответствии с принципом Ассура, выделим начальный механизм, обладающий числом степеней свободы всего исследуемого механизма. Этот механизм – кривошипный, состоит из стойки 0 и кривошипа 1 (рисунок 2). Остальные звенья образуют ведомую цепь, имеющую нулевую подвижность относительно звеньев начального механизма. Ведомая цепь, в свою очередь, состоит из двух двухзвенных структурных групп: 2 – 3 и 4 – 5.
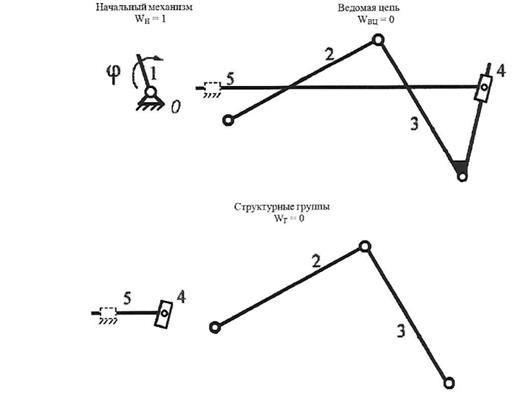
Рисунок 2 – Структурные группы механизма в соответствии с принципом Ассура.
Таким образом данный механизм состоит из одноподвижного начального механизма стойка 0 – кривошип 1 и двух структурных групп II класса, 2 порядка (ВВВ и ПВП).
3 КИНЕМАТИЧЕСКИЙ АНАЛИЗ МЕХАНИЗМА
ПОСТОЕНИЕ ПЛАНА ПОЛОЖЕНИЙ МЕХАНИЗМА
Рассмотрим механизм, изображенный на рис. 30. Размеры звеньев механизма и закон движения кривошипа приведены в таблице 2.
Таблица 2
| lOA , м | LАВ , м | LВС , м | Закон движения кривошипа 1, рад | ω, рад/с | i.передаточное число привода |
| 0.05 | 0.20 | 0.20 | φ = ωt | 280 | 12 |
Построим план положений механизма в масштабе 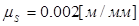 . За нулевое примем крайнее правое положение механизма; траектория точки A кривошипа 1 будет отображаться на плане положений окружностью радиуса ОА равного:
. За нулевое примем крайнее правое положение механизма; траектория точки A кривошипа 1 будет отображаться на плане положений окружностью радиуса ОА равного:
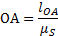
Где  – длина кривошипа 1;
– длина кривошипа 1;
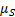 – масштаб положений механизма.
– масштаб положений механизма.
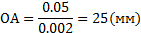
Разделив эту окружность на 12 равных частей, начиная от нулевого положения, выполним построение кинематической схемы механизма в соответствующих 12 положениях. Результат приведён на рисунке 3.
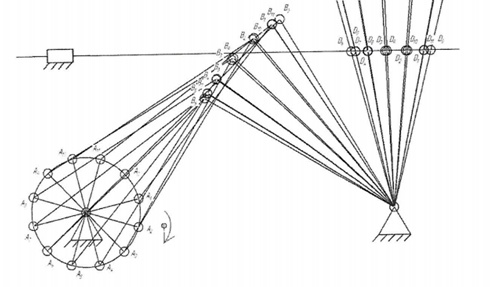
Рисунок 3 – План положений механизма.
3.2 ПОСТРОЕНИЕ КИНЕМАТИЧЕСКИХ ДИАГРАММ
Построим функцию положения механизма. На оси абсцисс отложим отрезки по 20 мм, соответствующие поворотам кривошипа 1 на каждые 300. Все 12 положений (полный оборот кривошипа) займут отрезок L =240 мм. Вдоль оси ординат отложим отрезки, соответствующие положениям точки Dсуппорта 5 относительно ее нулевого положения. Результат построений приведен на рисунке 4.
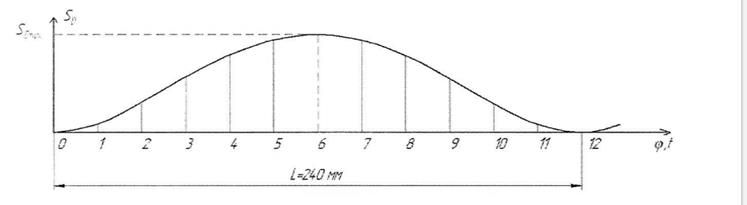
Рисунок 4 – Функция положения механизма.
Вычислим масштаб, в котором отложен угол φ поворота кривошипа 1:
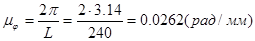
Масштаб времени t:
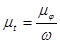
Где 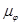 - масштаб, в котором отложен угол φ поворота кривошипа 1;
- масштаб, в котором отложен угол φ поворота кривошипа 1;
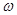 - угловая скорость вращения кривошипа 1.
- угловая скорость вращения кривошипа 1.
Найдём угловую скорость вращения кривошипа 1:
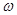 1
1 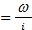
Где 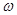 - угловая скорость на входе;
- угловая скорость на входе;
i – передаточное число привода.
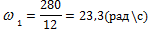
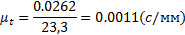
Таким образом, изображенный на рис. 4 график является не только функцией положения механизма S(φ), но и законом движения S(t) суппорта 5.
Найдем скорость VD суппорта 5 графическим методом. Так как скорость точки является производной по времени от ее перемещения, т.е. 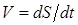 , то задача построения графика скорости точки D сводится к дифференцированию графика перемещения SD(t) по времени t. Для выполнения операции графического дифференцирования используем метод хорд. Результат выполнения приведён на рисунке 5.
, то задача построения графика скорости точки D сводится к дифференцированию графика перемещения SD(t) по времени t. Для выполнения операции графического дифференцирования используем метод хорд. Результат выполнения приведён на рисунке 5.
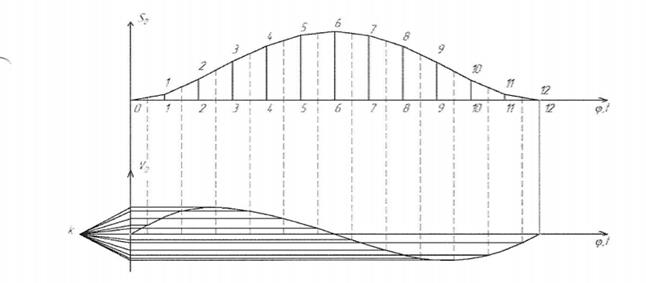
Рисунок 5 – Скорость точки D суппорта 5.
Вычислим масштаб скорости:
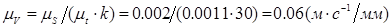
Где 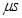 - масштаб, в котором построен план положений механизма;
- масштаб, в котором построен план положений механизма;
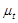 - масштаб времени;
- масштаб времени;
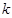 - длина вспомогательного отрезка.
- длина вспомогательного отрезка.
Найдем ускорение WDсуппорта 5 графическим методом. Для этого продифференцируем график скорости VD(t) по времени t. Для выполнения операции графического дифференцирования используем метод хорд. Результат выполнения приведён на рисунке 6.
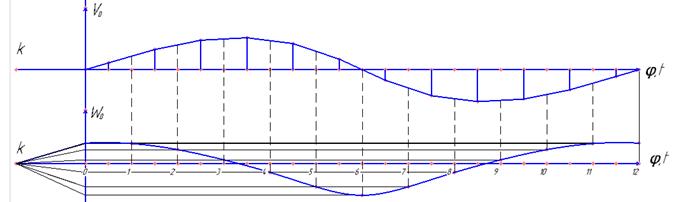
Рисунок 6 – Ускорение точки D суппорта 5.
Вычислим масштаб ускорения:
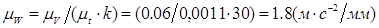
Где 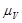 - масштаб скорости;
- масштаб скорости;
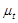 - масштаб времени;
- масштаб времени;
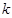 - длина вспомогательного отрезка.
- длина вспомогательного отрезка.
Таким образом на основе плана положений получены искомые кинематические диаграммы перемещения, скорости и ускорения суппорта станка для нарезания конических зубчатых колёс.
3.3 ПОСТРОЕНИЕ ПЛАНОВ СКОРОСТЕЙ
Вычислить скорость и ускорение суппорта 5 станка для нарезания конических зубчатых колёс в двух положениях(1,5). Рассмотрим первое положение механизма схематично изображенное на рисунке 7.
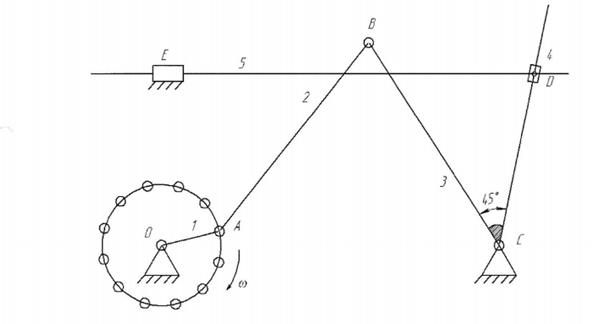
Рисунок 7 – первое положение станка для нарезания конических зубчатых колёс.
Исходные данные:
lOA=0.05(м)
lAB=lBC=0.2(м)
ω1=23,3(рад/с)
По теореме о сложении скоростей, можно записать:
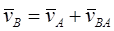
где 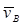 - абсолютная скорость точки B, принадлежащей шатуну 2 и кулисе 3;
- абсолютная скорость точки B, принадлежащей шатуну 2 и кулисе 3;
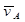 - абсолютная скорость точки A, принадлежащей кривошипу 1 и шатуну 2;
- абсолютная скорость точки A, принадлежащей кривошипу 1 и шатуну 2;
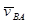 - скорость точки В относительно точки А.
- скорость точки В относительно точки А.
Найдем 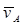 :
:
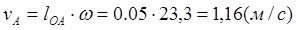
Где lOA– длина отрезка ОА;
ω1 – угловая скорость кривошипа 1.
Направление вектора 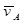 - перпендикуляр к OA в сторону вращения кривошипа 1. Скорости
- перпендикуляр к OA в сторону вращения кривошипа 1. Скорости 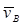 и
и 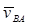 известны только по направлению:
известны только по направлению: 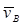 - перпендикуляр к ВС,
- перпендикуляр к ВС, 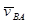 - перпендикуляр к АВ. Для вычисления величин этих векторов удобно воспользоваться методом векторных планов.
- перпендикуляр к АВ. Для вычисления величин этих векторов удобно воспользоваться методом векторных планов.
Пусть pv - полюс плана скоростей, тогда примем отрезок pva, отображающий
абсолютную скорость 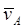 (рисунок 8),равным 30 мм. Вычислим масштаб плана скоростей:
(рисунок 8),равным 30 мм. Вычислим масштаб плана скоростей:
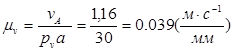
Где 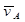 - абсолютная скорость точки A, принадлежащей кривошипу 1 и шатуну 2;
- абсолютная скорость точки A, принадлежащей кривошипу 1 и шатуну 2;
pva – отрезок, отображающий скорость 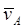 на плане скоростей.
на плане скоростей.
Согласно векторному уравнению через точку a проведем прямую, перпендикулярную АВ (направление скорости 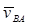 ) и через точку pv – прямую, перпендикулярную ВС (направление
) и через точку pv – прямую, перпендикулярную ВС (направление 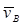 ). Таким образом, в результате пересечения прямых мы получим треугольник pvab, из которого можно найти длины отрезков скоростей
). Таким образом, в результате пересечения прямых мы получим треугольник pvab, из которого можно найти длины отрезков скоростей 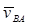 и
и 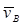 .
.
Рассмотрим теперь движение суппорта 5 и кулисы 3. Согласно теореме о сложении скоростей имеем:
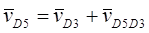
Где 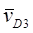 - абсолютная скорость точки D, принадлежащей кулисе 3;
- абсолютная скорость точки D, принадлежащей кулисе 3;
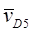 - переносная скорость точки D, принадлежащей суппорту 5;
- переносная скорость точки D, принадлежащей суппорту 5;
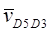 - относительная скорость точки D, принадлежащей кулисе 3 относительно точки D, принадлежащей суппорту 5.
- относительная скорость точки D, принадлежащей кулисе 3 относительно точки D, принадлежащей суппорту 5.
Отложим от очки pvгоризонтальную прямую в направлении движения суппорта 5. В направлении отрезка pvbчерез точку pvотложим прямую на угол 45°.
Найдём длину отрезка pvd3:
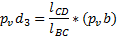
Где pvb – длина отрезка скорости 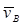 равного 19.42 мм. Находится путём измерения соответствующего отрезка на плане положений механизма;
равного 19.42 мм. Находится путём измерения соответствующего отрезка на плане положений механизма;
LCD и lBC – длины отрезков CDи BC(измеряются на плане положений механизма).
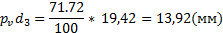
Через точку d3 проведём перпендикуляр отрезку pvd3прямую, показывающую направление скорости 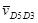 . Таким образом, мы получим замкнутый прямоугольный треугольник pvd3d5. План скоростей для данного положения механизма выполнен (рисунок 8).
. Таким образом, мы получим замкнутый прямоугольный треугольник pvd3d5. План скоростей для данного положения механизма выполнен (рисунок 8).
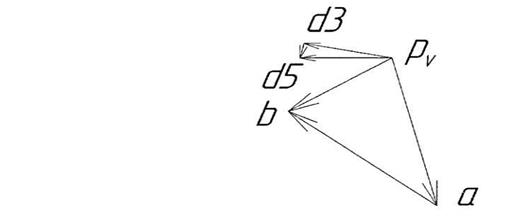
Рисунок 8 – план скоростей первого положения механизма для нарезания конических зубчатых колёс.
Теперь интересующие нас скорости точек звеньев найдём. Измеряя отрезки на плане скоростей и умножая полученные значения на масштаб плана скоростей:
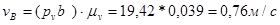
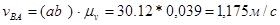
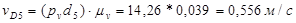
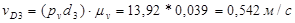
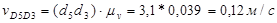
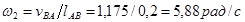
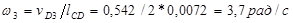
Таким образом, скорость суппорта 5 в положении, указанном на рисунке7, равна 1,16 м/с и направлена влево. Полученный результат соответствует исходным данным: действительно, согласно положению механизма на схеме, крайнее правое положение суппортом уже пройдено и он движется справа налево.
Аналогичным путём построим оставшийся план положения механизма и вычислим скорости звеньев. Результаты всех вычислений приведены в таблице 2.
Таблица 2
| Величина | Положения | |
| vAм/с | 1,16 | 1,16 |
| vBм/с | 0,76 | 0,422 |
| vBA м/с | 1,175 | 1,13 |
| vD5 м/с | 0,556 | 0,323 |
| vD3 м/с | 0,542 | 0,316 |
| vD5D3 м/с | 0,12 | 0,069 |
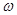 1 рад/с 1 рад/с | 23,3 | 23,3 |
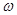 2 рад/с 2 рад/с | 5,88 | 5,65 |
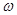 3 рад/с 3 рад/с | 3,7 | 2.2 |
3.4 ПОСТРОЕНИЕ ПЛАНОВ УСКОРЕНИЙ
Вычислим ускорение суппорта 5 станка для нарезания конических зубчатых колёс в двух положениях (1,5). Рассмотрим первое положение механизма, схематично изображенное на рисунке 7.
Т. к. шатун 2 совершает плоское движение, можно записать:
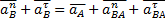 где
где 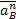 - нормальное ускорение точки В, принадлежащей шатуну 2 и кулисе 3;
- нормальное ускорение точки В, принадлежащей шатуну 2 и кулисе 3;
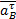 - касательное ускорение точки В, принадлежащей шатуну 2 и кулисе 3;
- касательное ускорение точки В, принадлежащей шатуну 2 и кулисе 3;
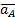 -абсолютное ускорение точки А, принадлежащей кривошипу 1 и шатуну 2;
-абсолютное ускорение точки А, принадлежащей кривошипу 1 и шатуну 2;
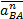 - нормальное ускорение точки В, относительно точки А;
- нормальное ускорение точки В, относительно точки А;
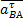 - касательное ускорение точки В относительно точки А.
- касательное ускорение точки В относительно точки А.
Вычислим значения этих ускорений:
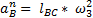
Где 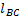 - длина отрезка ВС;
- длина отрезка ВС;
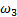 - угловое ускорение кулисы 3.
- угловое ускорение кулисы 3.
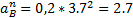
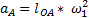
Где  - длина отрезка ОА;
- длина отрезка ОА;
ω1- угловое ускорение кривошипа 1
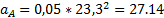
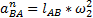
Где lAB– длина отрезка AB;
ω2 – угловое ускорение шатуна 2.
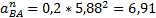
Таким образом в уравнении присутствуют два неизвестных по величине ускорения. Для их вычисления воспользуемся методом векторных планов.
Отложим от полюса плана ускорение pw отрезок pwa параллельный положению кривошипа 1, изображающий ускорение точки А кривошипа 1 (рисунок 9). Длину этого отрезка примем равной 30мм. Тогда масштаб плана ускорений будет следующим:
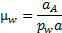
где 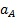 абсолютное ускорение точки А. кривошипа 1;
абсолютное ускорение точки А. кривошипа 1;
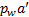 - длина отрезка, отображающего ускорение точки А на плане скоростей;
- длина отрезка, отображающего ускорение точки А на плане скоростей;
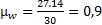 (м * с-2/мм)
(м * с-2/мм)
Переведем в отрезки известные нам по величине ускорения:
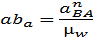
где 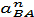 - нормальное ускорение точки В относительно точки А;
- нормальное ускорение точки В относительно точки А;
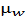 , - масштаб плана ускорений.
, - масштаб плана ускорений.
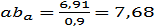 (мм)
(мм)
pwb = 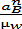
где 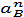 - нормальное ускорение точки В, принадлежащей шатуну 2 и коромыслу 3;
- нормальное ускорение точки В, принадлежащей шатуну 2 и коромыслу 3;
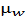 - масштаб плана ускорений.
- масштаб плана ускорений.
pwb = 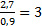 (мм)
(мм)
Через точку а проведем отрезок аbа, направленный параллельно АВ из точки В в точку А и равный 7.68 мм. Отрезок pwb, отображающий нормальное ускорение точки В, принадлежащей шатуну 2 и кулисе 3, длиной 3 мм отложим от точки pw и направим его параллельно ВС. Через точку b проведем прямую перпендикулярную ВС (направление ускорения 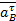 ), а через точку bа проведем прямую перпендикулярную АВ (направление ускорения
), а через точку bа проведем прямую перпендикулярную АВ (направление ускорения 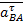 ). В результате пересечения прямых, мы получим точку bа* (b*). Таким образом, можно найти длины отрезков bb* и bаbа*, отображающих касательные ускорения
). В результате пересечения прямых, мы получим точку bа* (b*). Таким образом, можно найти длины отрезков bb* и bаbа*, отображающих касательные ускорения 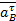 и
и 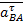 соответственно.
соответственно.
Рассмотрим движение суппорта 5 и кулисы 3. Согласно теореме о сложении ускорений имеем:
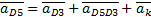
где 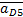 - ускорение точки D, принадлежащей суппорту 5;
- ускорение точки D, принадлежащей суппорту 5;
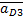 - ускорение точки D, принадлежащей кулисе 3;
- ускорение точки D, принадлежащей кулисе 3;
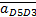 -Ускорение точки D суппорта 5 относительно точки D кулисы 3;
-Ускорение точки D суппорта 5 относительно точки D кулисы 3;
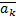 - ускорение Кориолиса.
- ускорение Кориолиса.
Найдем ускорение Кориолиса:
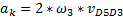
где 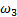 , - угловое ускорение кулисы 3;
, - угловое ускорение кулисы 3;
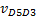 - относительная скорость точки D, принадлежащей суппорту 5 относительна точки D, принадлежащей кулисе 3.
- относительная скорость точки D, принадлежащей суппорту 5 относительна точки D, принадлежащей кулисе 3.
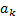 = 2 *3,7*0,12=0,888 (м/с2)
= 2 *3,7*0,12=0,888 (м/с2)
Вычислим значения длин отрезков соответствующих ускорений:
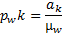
где 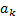 - ускорение Кориолиса;
- ускорение Кориолиса;
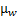 - масштаб плана ускорений.
- масштаб плана ускорений.
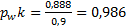 (мм)
(мм)
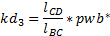
где 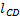 и
и 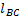 длины отрезков СD и ВС (измеряются на плане положений механизма);
длины отрезков СD и ВС (измеряются на плане положений механизма);
pwb* - длина отрезка, отображающего полное ускорение точки В.
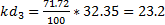 (мм)
(мм)
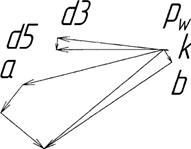
Отложив соответствующие отрезки согласно теореме о сложении ускорений, замкнем векторный многоугольник направлениями ускорений аD5 и аD5D3и в соответствии с уравнением, получим точку d5. Отрезокрwd5отображает на плане
ускорение суппорта 5. План скоростей для данного положения механизма


 выполнен (рисунок 9).
выполнен (рисунок 9).
Рисунок 9- План ускорения первого положения механизма станка для нарезания конических зубчатых колёс.
Теперь интересующие нас ускорения точек звеньев найдем, измеряяотрезки на плане ускорений и умножая полученные значения на масштаб плана ускорений:
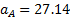 (м/с2)
(м/с2)
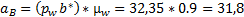 (м/с2)
(м/с2)
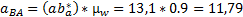 (м/с2)
(м/с2)
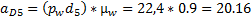 (м/с2)
(м/с2)
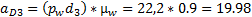 (м/с2)
(м/с2)
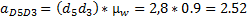 (м/с2)
(м/с2)
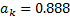 (м/с2)
(м/с2)
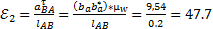 (рад/с2)
(рад/с2)
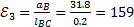 (рад/с2)
(рад/с2)
Таким образом, ускорение суппорта 5 в положении, указанном на рисунке 7, равно м/с2 и направлено влево. Полученный результат соответствуети
исходным данным: согласно положению механизма на схеме крайнее правое положение суппортом уже пройдено и он движется справа налево, ускоряясь.
Аналогичным путем построим оставшийся план положений механизма и вычислим ускорения звеньев. Результаты всех вычислений приведены в таблице 3.
Таблица 3.
| Величина | Положения | |
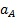 м/с2 м/с2 | 27.14 | 27,14 |
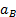 м/с2 м/с2 | 31,8 | 14,88 |
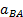 м/с2 м/с2 | 11,79 | |
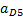 м/с2 м/с2 | 20.16 | 10,74 |
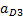 м/с2 м/с2 | 19.98 | 10,62 |
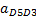 м/с2 м/с2 | 2.52 | 1,62 |
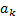 м/с2 м/с2 | 0.888 | 0,303 |
| ℰ1 рад/с2 | ||
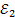 рад/с2 рад/с2 | 47.7 | 37,35 |
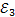 рад/с2 рад/с2 | 74,4 |
3.5 ВЫВОДЫ
Выполнив вычисления скоростей и ускорений точек механизма.сперва методом хорд, а затем методом векторных планов, были получены результаты. приведенные в таблице 4 и 5 соответственно. Согласно этим данным можно сделать вывод о том, что значения скоростей и ускорении, полученные двумя методами, практически идентичны, что говорит о верности результатов.
Таблица 4. Таблица 5.
| Величина | Положения | Величина | Положения | |||
| vD5м\с2 (метод векторных планов) | 0,556 | 0,323 |  м/с2 (метод векторных планов) м/с2 (метод векторных планов) | 20.16 | 10,74 | |
| vD5м\с2 (метод хорд) | 0,556 | 0,322 |  м/с2 (метод хорд) м/с2 (метод хорд) | 19,8 | 10,5 |
СИЛОВОЙ АНАЛИЗ МЕХАНИЗМА
