Вероятность того, что деталь находится только в одном ящике, равна 4 страница

Условный закон распределения можно задавать как функцией распределения так и плотностью распределения.

Условная плотность распределения вычисляется по формулам:

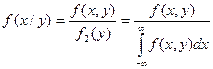
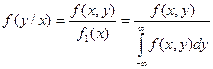
Условная плотность распределения обладает всеми свойствами плотности распределения одной случайной величины.

Условное математическое ожидание.

Определение. Условным математическим ожиданиемдискретной случайной величины Y при X = x (х – определенное возможное значение Х) называется произведение всех возможных значений Y на их условные вероятности.

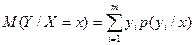
Для непрерывных случайных величин:

,

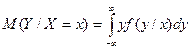где f(y/x) – условная плотность случайной величины Y при X=x.

Условное математическое ожидание M(Y/x)=f(x) является функцией от х и называется функцией регрессии Х на Y.

Пример. Найти условное математическое ожидание составляющей Y при

X= x₁=1 для дискретной двумерной случайной величины, заданной таблицей:

Y	X
x1=1	x2=3	x3=4	x4=8
y1=3	0,15	0,06	0,25	0,04
y2=6	0,30	0,10	0,03	0,07

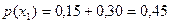
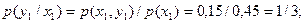
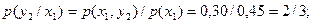
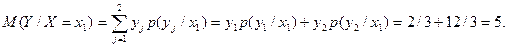
Аналогично определяются условная дисперсия и условные моменты системы случайных величин.

Зависимые и независимые случайные величины.

Случайные величины называются независимыми, если закон распределения одной из них не зависит от того какое значение принимает другая случайная величина.

Понятие зависимости случайных величин является очень важным в теории вероятностей.

Условные распределения независимых случайных величин равны их безусловным распределениям.

Определим необходимые и достаточные условия независимости случайных величин.

Теорема. Для того, чтобы случайные величины Х и Y были независимы, необходимо и достаточно, чтобы функция распределения системы (X, Y) была равна произведению функций распределения составляющих.

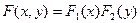
Аналогичную теорему можно сформулировать и для плотности распределения:

Теорема. Для того, чтобы случайные величины Х и Y были независимы, необходимо и достаточно, чтобы плотность совместного распределения системы (X, Y) была равна произведению плотностей распределения составляющих.

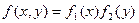
Определение. Корреляционным моментом m_xyслучайных величин Х и Y называется математическое ожидание произведения отклонений этих величин.

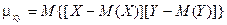
Практически используются формулы:

Для дискретных случайных величин: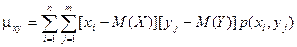

Для непрерывных случайных величин: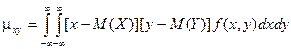

Корреляционный момент служит для того, чтобы охарактеризовать связь между случайными величинами. Если случайные величины независимы, то их корреляционный момент равен нулю.

Корреляционный момент имеет размерность, равную произведению размерностей случайных величин Х и Y. Этот факт является недостатком этой числовой характеристики, т.к. при различных единицах измерения получаются различные корреляционные моменты, что затрудняет сравнение корреляционных моментов различных случайных величин.

Для того, чтобы устранить этот недостаток применятся другая характеристика – коэффициент корреляции.

Определение. Коэффициентом корреляции r_xy случайных величин Х и Y называется отношение корреляционного момента к произведению средних квадратических отклонений этих величин.

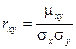
Коэффициент корреляции является безразмерной величиной. Коэффициент корреляции независимых случайных величин равен нулю.

Свойство: Абсолютная величина корреляционного момента двух случайных величин Х и Y не превышает среднего геометрического их дисперсий.

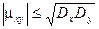
Свойство: Абсолютная величина коэффициента корреляции не превышает единицы.

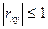
Случайные величины называются коррелированными, если их корреляционный момент отличен от нуля, и некоррелированными, если их корреляционный момент равен нулю.

Если случайные величины независимы, то они и некоррелированы, но из некоррелированности нельзя сделать вывод о их независимости.

Если две величины зависимы, то они могут быть как коррелированными, так и некоррелированными.

Часто по заданной плотности распределения системы случайных величин можно определить зависимость или независимость этих величин.

Наряду с коэффициентом корреляции степень зависимости случайных величин можно охарактеризовать и другой величиной, которая называется коэффициентом ковариации. Коэффициент ковариации определяется формулой:

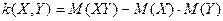
Пример. Задана плотность распределения системы случайных величин Х и Y.

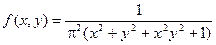
Выяснить являются ли независимыми случайные величины Х и Y.

Для решения этой задачи преобразуем плотность распределения:

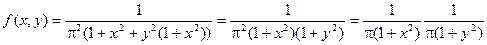
Таким образом, плотность распределения удалось представить в виде произведения двух функций, одна из которых зависит только от х, а другая – только от у. Т.е. случайные величины Х и Y независимы. Разумеется, они также будут и некоррелированы.

Линейная регрессия.

Рассмотрим двумерную случайную величину (X, Y), где X и Y – зависимые случайные величины.

Представим приближенно одну случайную величину как функцию другой. Точное соответствие невозможно. Будем считать, что эта функция линейная.

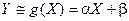
Для определения этой функции остается только найти постоянные величины a и b.

Определение. Функция g(X) называется наилучшим приближением случайной величины Y в смысле метода наименьших квадратов, если математическое ожидание

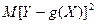принимает наименьшее возможное значение. Также функция g(x) называется среднеквадратической регрессиейY на X.

Теорема. Линейная средняя квадратическая регрессия Y на Х вычисляется по формуле:

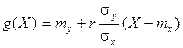
в этой формуле m_x=M(X), m_y=M(Y), 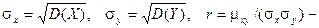коэффициент корреляции величин Х и Y.

Величина 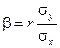называется коэффициентом регрессииY на Х.

Прямая, уравнение которой

,

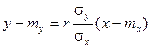называется прямой сренеквадратической регрессииY на Х.

Величина 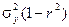называется остаточной дисперсиейслучайной величины Y относительно случайной величины Х. Эта величина характеризует величину ошибки, образующейся при замене случайной величины Y линейной функцией g(X)=aХ + b.

Видно, что если r=±1, то остаточная дисперсия равна нулю, и, следовательно, ошибка равна нулю и случайная величина Y точно представляется линейной функцией от случайной величины Х.

Прямая среднеквадратичной регрессии Х на Y определяется аналогично по формуле:

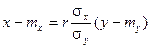
Прямые среднеквадратичной регрессии пересекаются в точке (т_х, т_у), которую называют центром совместного распределенияслучайных величин Х и Y.

Линейная корреляция.

Если две случайные величины Х и Y имеют в отношении друг друга линейные функции регрессии, то говорят, что величины Х и Y связаны линейной корреляционной зависимостью.

Теорема. Если двумерная случайная величина (X, Y) распределена нормально, то Х и Y связаны линейной корреляционной зависимостью.

Закон больших чисел.

Неравенство Чебышева.

(Чебышев Пафнутий Львович (1821 – 1824) – русский математик)

На практике сложно сказать какое конкретное значение примет случайная величина, однако, при воздействии большого числа различных факторов поведение большого числа случайных величин практически утрачивает случайный характер и становится закономерным.

Этот факт очень важен на практике, т.к. позволяет предвидеть результат опыта при воздействии большого числа случайных факторов.

Однако, это возможно только при выполнении некоторых условий, которые определяются законом больших чисел. К законам больших чисел относятся теоремы Чебышева (наиболее общий случай) и теорема Бернулли (простейший случай), которые будут рассмотрены далее.

Рассмотрим дискретную случайную величину Х (хотя все сказанное ниже будет справедливо и для непрерывных случайных величин), заданную таблицей распределения:

X	x1	x2	…	xn
p	p1	p2	…	pn

Требуется определить вероятность того, что отклонение значения случайной величины от ее математического ожидания будет не больше, чем заданное число e.

Теорема. (Неравенство Чебышева) Вероятность того, что отклонение случайной величины Х от ее математического ожидания по абсолютной величине меньше положительного числа e, не меньше чем .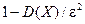

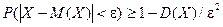
Доказательство этой теоремы приводить не будем, оно имеется в литературе.

Теорема Чебышева.

Теорема. Если Х₁, Х₂, …, Х_n- попарно независимые случайные величины, причем дисперсии их равномерно ограничены (не превышаю постоянного числа С), то, как бы мало не было положительное число e, вероятность неравенства

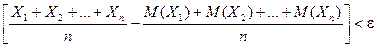
будет сколь угодно близка к единице, если число случайных величин достаточно велико.

Т.е. можно записать:

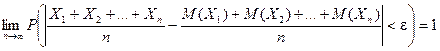
ЛЕКЦИЯ 6.

Часто бывает, что случайные величины имеют одно и то же математическое ожидание. В этом случае теорема Чебышева несколько упрощается:

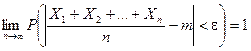
Дробь, входящая в записанное выше выражение есть не что иное как среднее арифметическое возможных значений случайной величины.

Теорема утверждает, что хотя каждое отдельное значение случайной величины может достаточно сильно отличаться от своего математического ожидания, но среднее арифметическое этих значений будет неограниченно приближаться к среднему арифметическому математических ожиданий.

Отклоняясь от математического ожидания как в положительную так и в отрицательную сторону, от своего математического ожидания, в среднем арифметическом отклонения взаимно сокращаются.

Таким образом, величина среднего арифметического значений случайной величины уже теряет характер случайности.

Теорема Бернулли.

Пусть производится п независимых испытаний, в каждом из которых вероятность появления события А равно р.

Возможно определить примерно относительную частоту появления события А.

Теорема. Если в каждом из п независимых испытаний вероятность р появления события А постоянно, то сколь угодно близка к единице вероятность того, что отклонение относительной частоты от вероятности р по абсолютной величине будет сколь угодно малым, если число испытаний р достаточно велико.

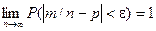
Здесь т – число появлений события А. Из всего сказанного выше не следует, что с увеличением число испытаний относительная частота неуклонно стремится к вероятности р, т.е. 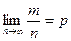. В теореме имеется в виду только вероятность приближения относительной частоты к вероятности появления события А в каждом испытании.

В случае, если вероятности появления события А в каждом опыте различны, то справедлива следующая теорема, известная как теорема Пуассона.

Теорема. Если производится п независимых опытов и вероятность появления события А в каждом опыте равна р_i, то при увеличении п частота события А сходится по вероятности к среднему арифметическому вероятностей р_i.

Предельные теоремы.

Как уже говорилось, при достаточно большом количестве испытаний, поставленных в одинаковых условиях, характеристики случайных событий и случайных величин становятся почти неслучайными. Это позволяет использовать результаты наблюдений случайных событий для предсказания исхода того или иного опыта.

Предельные теоремы теории вероятностей устанавливают соответствие между теоретическими и экспериментальными характеристиками случайных величин при большом количестве испытаний.

В рассмотренном выше законе больших чисел нечего не говорилось о законе распределения случайных величин.

Поставим задачу нахождения предельного закона распределения суммы

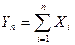
когда число слагаемых п неограниченно возрастает. Эту задачу решает Центральная предельная теорема Ляпунова, которая была сформулирована выше.

В зависимости от условий распределения случайных величин X_i, образующих сумму, возможны различные формулировки центральной предельной теоремы.

Допустим, что случайные величины X_i взаимно независимы и одинаково распределены.

Теорема. Если случайные величины X_i взаимно независимы и имеют один и тот же закон распределения с математическим ожиданием т и дисперсией s², причем существует третий абсолютный момент n₃, то при неограниченном увеличении числа испытаний п закон распределения суммы 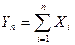неограниченно приближается к нормальному.

При доказательстве этой теоремы Ляпуновым использовались так называемые характеристические функции.

Определение. Характеристической функциейслучайной величины Х называется функция

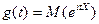
эта функция представляет собой математическое ожидание некоторой комплексной случайной величины 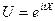, являющейся функцией от случайной величины Х. При решении многих задач удобнее пользоваться характеристическими функциями, а не законами распределения.

Зная закон распределения, можно найти характеристическую функцию по формуле (для непрерывных случайных величин):

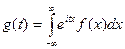
Как видим, данная формула представляет собой не что иное, как преобразование Фурье для функции плотности распределения. Очевидно, что с помощью обратного преобразования Фурье можно по характеристической функции найти закон распределения.

Введение характеристических функций позволяет упростить операции с числовыми характеристиками случайных величин.

В случае нормального распределения характеристическая функция имеет вид:

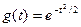
Сформулируем некоторые свойства характеристических функций:

1) Если случайные величины Х и Y связаны соотношением

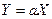
где а – неслучайный множитель, то

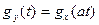
2) Характеристическая функция суммы независимых случайных величин равна произведению характеристических функций слагаемых.

Случайные величины X_i, рассмотренные в центральной предельной теореме, могут обладать произвольными распределениями вероятностей.

Если все эти случайные величины одинаково распределены, дискретны и принимают только два возможных значения 0 или 1, то получается простейший случай центральной предельной теоремы, известный как теорема Муавра – Лапласа.

Теорема. (Теорема Муавра – Лапласа) Если производится п независимых опытов, в каждом из которых событие А появляется с вероятностью р, то для любого интервала (a, b) справедливо соотношение:

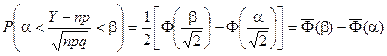
где Y – число появлений события А в п опытах, q = 1 – p, Ф(х) – функция Лапласа, 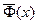- нормированная функция Лапласа .

Теорема Муавра – Лапласа описывает поведение биноминального распределения при больших значениях п.

Данная теорема позволяет существенно упростить вычисление по формуле биноминального распределения.

Расчет вероятности попадания значения случайной величины в заданный интервал 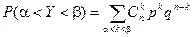при больших значениях п крайне затруднителен. Гораздо проще воспользоваться формулой:

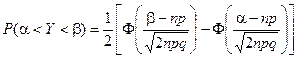
Теорема Муавра – Лапласа очень широко применяется при решении практических задач.

Пример. Вероятность наступления события А в каждом испытании равна 0,3. Используя неравенство Чебышева, оценить вероятность того, что в 10000 испытаниях отклонение относительной частоты появления события А от его вероятности не превзойдет по абсолютной величине 0,01.

В соответствии с неравенством Чебышева вероятность того, что отклонение случайной величины от ее математического ожидания будет меньше некоторого числа e, ограничена в соответствии с неравенством .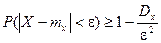

Надо определить математическое ожидание и дисперсию числа появления события А при одном опыте. Для события А случайная величина может принимать одно из двух значений: 1- событие появилось, 0- событие не появилось. При этом вероятность значения 1 равна вероятности р=0,3, а вероятность значения 0- равна вероятности ненаступления события А

q=1 – p =0,7.

По определению математического ожидания имеем:

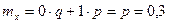
Дисперсия: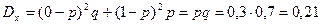

В случае п независимых испытаний получаем 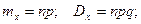Эти формулы уже упоминались выше.

В нашем случае получаем: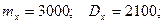

Вероятность отклонения относительной частоты появления события А в п испытаниях от вероятности на величину, не превышающую e=0,01 равна:

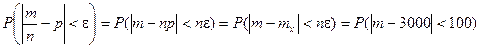
Выражение полученное в результате этих простых преобразований представляет собой не что иное, как вероятность отклонения числа т появления события А от математического ожидания на величину не большую, чем d=100.

В соответствии с неравенством Чебышева эта вероятность будет не меньше, чем величина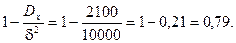

Пример. Сколько следует проверить деталей, чтобы с вероятностью, не меньшей 0,96, можно было ожидать, что абсолютная величина отклонения относительной частоты годных деталей от вероятности детали быть годной, равной 0,98, не превысит 0,02.

Условие задачи фактически означает, что выполняется неравенство:

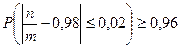
Здесь п- число годных деталей, т- число проверенных деталей. Для применения неравенства Чебышева преобразуем полученное выражение:

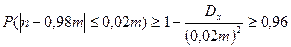
После домножения выражения, стоящего в скобках, на т получаем вероятность отклонения по модулю количества годных деталей от своего математического ожидания, следовательно, можно применить неравенство Чебышева, т.е. эта вероятность должна быть не меньше, чем величина 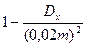, а по условию задачи еще и не меньше, чем 0,96.

Таким образом, получаем неравенство 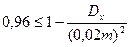. Как уже говорилось в предыдущей задаче, дисперсия может быть найдена по формуле .

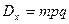Итого, получаем: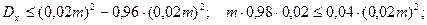

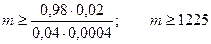
Т.е. для выполнения требуемых условий необходимо не менее 1225 деталей.

Пример. Суточная потребность электроэнергии в населенном пункте является случайной величиной, математическое ожидание которой равно 3000 кВт/час, а дисперсия составляет 2500. Оценить вероятность того, что в ближайшие сутки расход электроэнергии в этом населенном пункте будет от 2500 до 3500 кВт/час.

Требуется найти вероятность попадания случайной величины в заданный интервал:

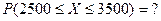
Крайние значения интервала отклоняются от математического ожидания на одну и ту же величину, а именно – на 500. Тогда можно записать с учетом неравенства Чебышева:

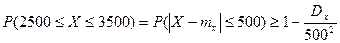
Отсюда получаем:

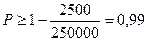
Т.е. искомая вероятность будет не меньше, чем 0,99.

Пример. Среднее квадратическое отклонение каждой из 2500 независимых случайных величин не превосходит 3. Оценить вероятность того, что абсолютная величина отклонения среднего арифметического этих случайных величин от среднего арифметического их математических ожиданий не превосходит 0,3.

Требуется найти вероятность

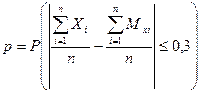
Неравенство Чебышева в случае суммы случайных величин имеет вид:

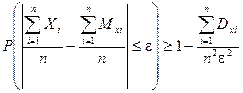
Если среднее квадратическое отклонение не превосходит 3, то, очевидно, дисперсия не превосходит 9. Величина e по условию задачи равна 0,3.

Тогда 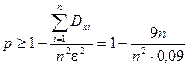. Отсюда получаем при n=2500:

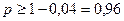
Пример. Выборочным путем требуется определить среднюю длину изготавливаемых деталей. Сколько нужно исследовать деталей, чтобы с вероятностью, большей чем 0,9, можно было утверждать, что средняя длина отобранных изделий будет отличаться от математического ожидания этого среднего (средняя длина деталей всей партии) не более, чем на 0,001 см.? Установлено, что среднее квадратическое отклонение длины детали не превышает 0,04 см.