Методические указания по выполнению контрольной работы. по дисциплине «Линейная алгебра»

ВАРИАНТЫ КОНТРОЛЬНОЙ РАБОТЫ

по дисциплине «Линейная алгебра»

для студентов первого курса бакалавриата, обучающихся по направлениям «Экономика» и «Бизнес-информатика»

Ниже приводятся только варианты контрольных работ по данной дисциплине и указания по их выполнению, взятые из пособия: Линейная алгебра. Учебно-методическое пособие для студентов первого курса бакалавриата, обучающихся по направлениям 080100.62 «Экономика» и 080700.62 «Бизнес-информатика» / Под ред. проф. Н.Ш. Кремера. – М.: ВЗФЭИ, 2011.

Полностью указанное пособие приводится в Интернет-репозитории института ( http://repository.vzfei.ru ). В этом пособии, кроме приведенных здесь вариантов контрольных работ и указаний по их выполнению, представлены методические рекомендации по изучению дисциплины, типовые задачи (с решениями и для самоподготовки) и вопросы для самопроверки.

Методические указания по выполнению контрольной работы

В соответствии с учебным планом по дисциплине «Линейная алгебра» каждый студент должен выполнить одну домашнюю контрольную работу №1 (по приведенным в данной брошюре вариантам) в сроки, установленные учебным графиком.

По контрольной работе студенты вечерних и дневных групп проходят собеседование. На собеседовании выясняется, насколько глубоко усвоен пройденный материал и соответствуют ли знания студента и его навыки в решении задач качеству представленной работы. Зачет по каждой контрольной работе студенты получают лишь после успешного прохождения собеседования.

Номер варианта контрольной работы определяется по последней цифре номера личного дела студента, который совпадает с номером его зачетной книжки и студенческого билета.

Сроки представления домашней контрольной работы на проверку указаны в индивидуальном графике студента, а для студентов дневных групп также сообщаются во время осенней установочной сессии. Однако эти сроки являются крайними. Чтобы работа была своевременно проверена, а при необходимости доработана и сдана повторно, ее надлежит представить значительно раньше указанного срока. Студентам дневных групп рекомендуется свою домашнюю контрольную работу выполнять во время установочной сессии, на которой излагается учебный материал. Это даст возможность студенту использовать свое пребывание в институте для консультаций по всем возникшим при выполнении работы вопросам. После окончания сессии в течение двух недель работу необходимо окончательно завершить, а затем представить на проверку.

Если в ходе написания работы у студента появятся вопросы или затруднения в решении задач контрольного задания, он может обратиться в институт за устной или письменной консультацией (например, по электронной почте на форум кафедры).

При изучении учебного материала и подготовке к контрольным работам рекомендуется использовать учебники и учебные пособия, электронные ресурсы, приведенные выше в разделе «Литература», а также данную брошюру.

После проверки контрольная работа студента получает оценку «Допускается к собеседованию» или «Не допускается к собеседованию».

Контрольная работа содержит набор заданий, при выполнении которых необходимо соблюдать следующие правила.

1. Работа должна быть выполнена в школьной тетради, имеющей широкие (не менее 3 см) поля для замечаний рецензента.

2. На обложке тетради следует указать фамилию, имя, отчество (полностью), факультет, специальность, курс, номер личного дела, вариант и номер контрольной работы, а также фамилию преподавателя к которому направляется данная работа на проверку.

3. Перед решением каждой задачи нужно привести (распечатать) полностью ее условие.

4. Следует придерживаться той последовательности при решении задач, в какой они даны в задании, строго сохраняя при этом нумерацию примеров (задач).

5. Не допускается замена задач контрольной работы другими заданиями.

6. Решения задач должны сопровождаться развернутыми пояснениями, нужно привести в общем виде используемые формулы с объяснением употребляемых обозначений, а окончательный ответ следует выделить.

7. Чертеж к задаче 5 должен быть выполнен в прямоугольной системе координат в полном соответствии с данными условия задачи и теми результатами, которые получены.

8. В конце работы приводится список использованной литературы (указывают автора, название, издательство, год издания), ставится дата окончания работы и подпись.

9. Если вычисления, выполняемые при решении задач, приближенные, то следует придерживаться правил приближенных вычислений, которые приведены в [3, §5.7] или в учебно-методическом пособии для студентов первого курса бакалавриата «Математический анализ. Математика1 / под. ред. Н.Ш. Кремера – М.: ВЗФЭИ, 2011 (с.5 – 8).

Если работа получила в целом положительную оценку («Допускается к собеседованию»), но в ней есть отдельные недочеты (указанные в тетради), то нужно сделать соответствующие исправления и дополнения в той же тетради (после имеющихся решений и записи «Работа над ошибками») и предъявить доработку на собеседовании. Если работа «Не допускается к собеседованию», ее необходимо в соответствии с требованиями преподавателя частично или полностью переделать. Повторную работу надо выполнить в той же тетради (если есть место) или в новой с надписью на обложке «Повторная», указав фамилию преподавателя, которым работа была ранее не зачтена. Вместе с незачтенной работой, повторную работу представить снова на проверку.

Контрольная работа не зачитывается, если ее вариант не совпадает с последней цифрой номера личного дела студента или она выполнена по вариантам прошлых лет.

Студенты, не получившие зачета по контрольной работе, к экзамену не допускаются. Если в соответствии с учебным графиком контрольная работа должна быть выполнена с частичным использованием КОПР, то для получения зачета по этой работе необходимо дополнительно представить протокол ответа студента о работе с КОПР. Зачтенные работы предъявляются на экзамене и не подлежат возвращению после успешной сдачи экзамена.

ВАРИАНТЫ КОНТРОЛЬНОЙ РАБОТЫ[1] №1

ВАРИАНТ 1

(для студентов, номера личных дел которых оканчиваются цифрой 1)

1. Даны матрицы:

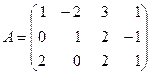и

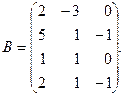
Найти матрицу 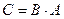и выяснить, являются ли строки матрицы С линейно зависимыми.

2. Методом обратной матрицы решить систему уравнений:

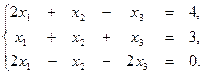
3. Методом Гаусса решить систему уравнений:

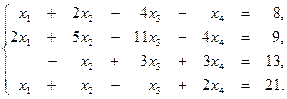
Найти одно из ее базисных решений.

4. Записать квадратичную форму 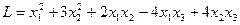в матричном виде. Привести ее к каноническому виду.

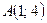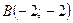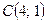5. Точки , и являются вершинами треугольника ABC. Составить уравнение высоты треугольника, опущенной из точки А на сторону ВС. Определить координаты точки Н – основания высоты АН треугольника АВС. Сделать чертеж.

6. Найти значение параметра 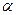, при котором плоскост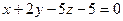и и 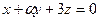будут перпендикулярны.

ВАРИАНТ 2

(для студентов, номера личных дел которых оканчиваются цифрой 2)

1. Даны матрицы:

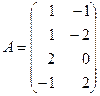и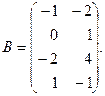

Найти матрицу 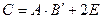и выяснить, имеет ли она обратную.

2. Методом Гаусса решить систему уравнений:

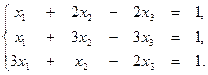
3. Выяснить, является ли совместной система уравнений:

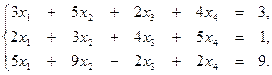
4. Найти собственные значения и собственные векторы линейного оператора 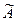, заданного матрицей .

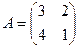5. Определить вид и расположение кривой второго порядка 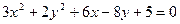, приведя ее уравнение к каноническому виду. Составить уравнение прямой, проходящей через центр кривой второго порядка и точку 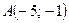. Сделать чертеж.

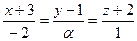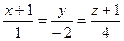6. Найти значение параметра α, при котором прямые и будут перпендикулярны.

ВАРИАНТ 3

(для студентов, номера личных дел которых оканчиваются цифрой 3)

1. Решить матричное уравнение

,

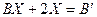где

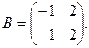
2. По формулам Крамера решить систему уравнений:

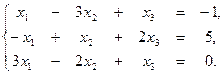
3. Методом Гаусса решить систему уравнений:

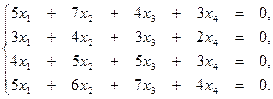
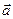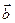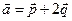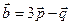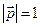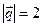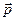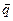4. Найти угол между векторами и , если известно, что , , , и угол между векторами и равен .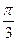

5. Определить вид и расположение кривой второго порядка 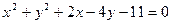. Составить уравнение прямой, проходящей через ее центр перпендикулярно прямой 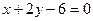. Сделать чертеж.

6. Найти угол между прямой 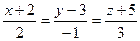и плоскостью .

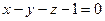ВАРИАНТ 4

(для студентов, номера личных дел которых оканчиваются цифрой 4)

1. Даны матрицы:

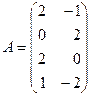и

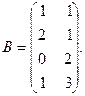
Найти матрицу 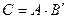и определить ее ранг.

2. Методом обратной матрицы решить систему уравнений:

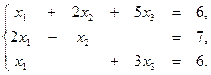
3. Методом Гаусса решить систему уравнений:

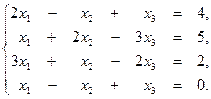
4. Проверить, что векторы 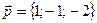, 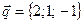и 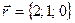образуют базис в пространстве .

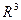5. Определить вид и расположение кривой второго порядка 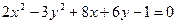, приведя ее уравнение к каноническому виду. Найти уравнение прямой, проходящей через центр кривой второго порядка и точку 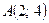. Сделать чертеж.

6. Составить уравнение плоскости, проходящей через точк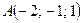и и 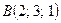параллельно оси .

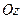ВАРИАНТ 5

(для студентов, номера личных дел которых оканчиваются цифрой 5)

1. Решить матричное уравнение

,

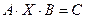где

, ,

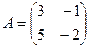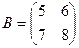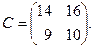
2. По формулам Крамера решить систему уравнений:

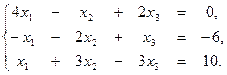
3. Методом Гаусса решить систему уравнений:

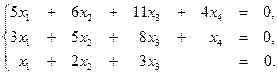
4. Найти вектор 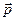, коллинеарный вектору 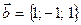, такой что скалярное произведение 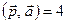, если известно, что вектор .

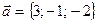5. Определить вид и расположение кривой второго порядка , приведя ее уравнение к каноническому виду. Составить уравнение прямой, проходящей через вершину кривой второго порядка и точку 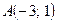. Сделать чертеж.

6. Составить уравнение плоскости, проходящей через точку 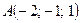и перпендикулярной вектору .

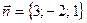ВАРИАНТ 6

(для студентов, номера личных дел которых оканчиваются цифрой 6)

1. Даны матрицы:

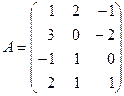и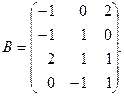

Найти матрицу 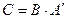и выяснить, имеет ли она обратную.

2. Методом Гаусса решить систему уравнений:

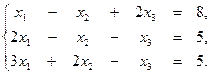
3. Выяснить, является ли совместной система уравнений:

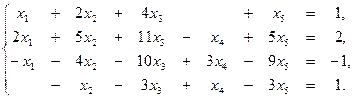
4. Записать квадратичную форму 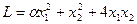в матричном виде. Определить значения параметра a, при которых квадратичная форма является знакоопределенной.

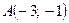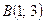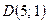5. Точки , и являются вершинами параллелограмма ABCD. Найти уравнения сторон АВ и AD и координаты четвертой вершины С, противолежащей вершине А. Сделать чертеж.

6. Найти значения параметров α и b, при которых плоскост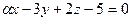и и 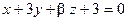будут параллельны.

ВАРИАНТ 7

(для студентов, номера личных дел которых оканчиваются цифрой 7)

1. Решить матричное уравнение

,

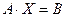где

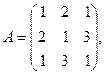
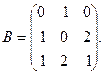
2. По формулам Крамера решить систему уравнений:

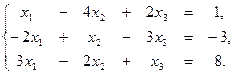
3. Методом Гаусса решить систему уравнений:

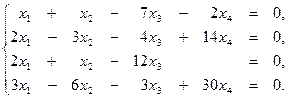
4.Проверить, что вектор 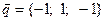является собственным вектором линейного оператора 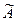, заданного матрицей 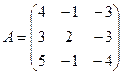. Найти собственное значение оператора 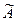, соответствующее данному вектору.

5.Составить уравнение прямой, проходящей через центр кривой второго порядка 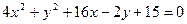перпендикулярно прямой 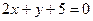. Сделать чертеж.

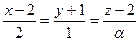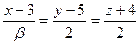6. Найти значение параметров α и b, при которых прямые и будут параллельны.

ВАРИАНТ 8

(для студентов, номера личных дел которых оканчиваются цифрой8)

1. Даны матрицы:

,

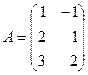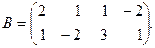
Найти матрицу 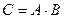и определить ее ранг.

2. Методом обратной матрицы решить систему уравнений:

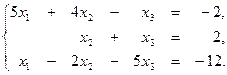
3. Методом Гаусса решить систему уравнений:

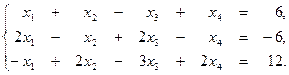
Найти одно из ее базисных решений.

4. Проверить, что векторы 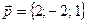, 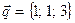и 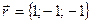образуют базис в пространстве .

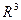5. Определить вид и расположение кривой второго порядка 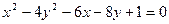. Составить уравнение прямой, проходящей через центр кривой второго порядка параллельно прямой 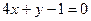. Сделать чертеж.

6. Найти угол между плоскостям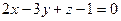и и .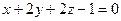

ВАРИАНТ 9

(для студентов, номера личных дел которых оканчиваются цифрой9)

1. Решить матричное уравнение

,

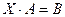где

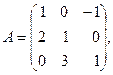
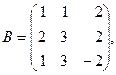
2. По формулам Крамера решить систему уравнений:

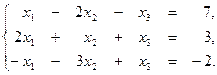
3. Методом Гаусса решить систему уравнений:

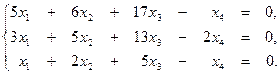
4. При каком значении параметра aвектор, 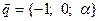, является собственным вектором линейного оператора 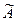, заданного матрицей 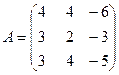. Найти собственное значение оператора 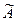, соответствующее данному вектору.

5. Составить уравнение прямой, проходящей через центр окружности 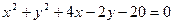параллельно прямой 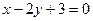. Сделать чертеж.

6. Составить уравнение плоскости, перпендикулярной прямой 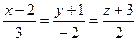и проходящей через точку .

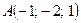ВАРИАНТ 10

(для студентов, номера личных дел которых оканчиваются цифрой 0)

1. При каких значениях 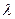ранг матрицы

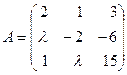
равен двум?

2. Методом обратной матрицы решить систему уравнений:

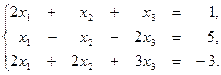
3. Методом Гаусса решить систему уравнений:

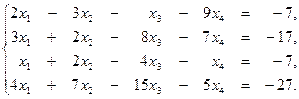
Найти одно из ее базисных решений.

4. При каком значении параметра α, векторы 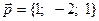, , 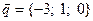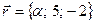будут линейно зависимыми?

5. Определить вид и расположение кривой второго порядка 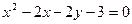, приведя ее уравнение к каноническому виду. Составить уравнение прямой, проходящей через вершину кривой второго порядка параллельно прямой 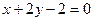. Сделать чертеж.

6. Составить уравнение плоскости, проходящей через точку 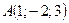и параллельной плоскости .

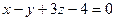[1] Напоминаем, что номер личного дела совпадает с номером студенческого билета и зачетной книжки студента