И значительных деформациях
Магистральные трещины характерны тем, что распространяются на всю высоту стены, разделяя ее на отдельные части. Причиной образования таких трещин обычно является неравномерная осадка фундаментов или большие температурные деформации здания. С образованием магистральных трещин коробка здания как бы разделяется на отдельные блоки, деформируемые самостоятельно при силовых и температурных воздействиях. Если трещины образуются в углах здания, то возможна потеря устойчивости или отрыв торцевой стены.
Традиционным способом усиления стен при потере устойчивости является устройство кирпичных или железобетонных контрфорсов, которые устанавливают на всю высоту стены или часть ее. Под контрфорсы устраивают отдельные фундаменты, проверяемые расчетом на прочность, скольжение и опрокидывание.
При значительных деформациях здания и наличии магистральных трещин для усиления стен применяют металлические напряженные пояса, устанавливаемые на уровне междуэтажных перекрытий. Способы усиления стен при магистральных трещинах представлены в табл.4.9.
Практика показывает, что металлическим поясом (бандажом) можно усиливать как отдельные стены, так и коробку здания в целом.
Таблица 4.9
Усиление стен при магистральных трещинах
| № п/п | Способы усиления. Эскиз усиления | Элементы усиления | |
| № поз. | Материал, размеры | ||
Усиление контрфорсами 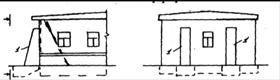 | Железобетонный контрфорс δ=300…500 | ||
Усиление поясом отдельной стены 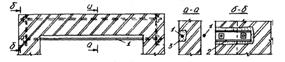 | Тяж Ø20…30 Накладка [ 12...16 Бетон кл. В25 | ||
Усиление поясом коробки здания 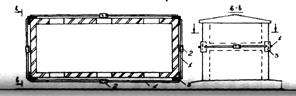 | Тяж Ø20…30 Стяжная муфта Ø20…30 Накладка L 100х8 (L 140х10) |
В первом случае пояс состоит из стальных тяжей круглого профиля, располагаемых на внутренней и наружной поверхностях стены, и опорных балок швеллерного или коробчатого типов. Натяжение пояса производят гайками в торце стены.
Во втором случае пояс состоит из тяжей и уголков, однако тяжи преимущественно располагают на наружной поверхности стен. Натяжение пояса осуществляют с помощью стальных муфт с правой и левой резьбой, размещаемых в средней части тяжей. Усилие натяжения пояса в обоих случаях контролируют по показаниям динамометрического ключа, а при отсутствии его - по внешним признакам. При нормальном натяжении тяжи не провисают и при легком ударе молотка издают звук высокого тона.
Нужно отметить, что в процессе эксплуатации усилие в поясах непостоянно и изменяется при колебаниях температуры внешней среды. Для стабилизации усилий натяжения пояса автором разработаны стабилизирующие устройства, конструкция и методика расчета которых рассмотрены в третьей главе.
Для сохранения облика фасадов, если это позволяет толщина стен, элементы пояса укладывают в заблаговременно устроенные штрабы сечением 70x80 мм, которые после монтажа и натяжения пояса заделывают кирпичом и оштукатуривают.
Расчет сечения поясов, как показывает опыт, - достаточно сложная инженерная задача, правильное решение которой зависит от целого ряда параметров, среди которых геологические характеристики грунта основания, вид магистральной трещины, прочностные характеристики каменной кладки и пр. В практических расчетах усилие, по которому устанавливают площадь поперечного сечения тяжей, обычно определяют по приближенной формуле
N=0,2Rsqlδ
где Rsq - расчетное сопротивление кладки на срез по неперевязанному шву;
l, δ - соответственно длина и толщина стены;
0,2 - эмпирический (понижающий) коэффициент.
Анализ показывает, что при значительной протяженности здания использование указанной формулы приводит к большому перерасходу металла на усиление. Более экономичное решение достигается при расчете поясов из условия равновесия моментов по методике, разработанной на кафедре строительных конструкций Пензенской ГАСА. Следует, однако, подчеркнуть, что выбор расчетной схемы и методика решения данной задачи всегда индивидуальны и зависят главным образом от характера трещин и причин, побуждающих раскрытие.
Проектирование стальных поясов
Стальные пояса (бандажи) предназначаются для усиления кирпичных зданий с вертикальной или наклонной трещиной (трещинами) в несущих стенах, образовавшейся в результате неравномерной осадки ленточного фундамента.
В основу расчета поясов положены следующие предпосылки:
- нагрузка на основание фундамента по длине здания распределена равномерно;
- сжимаемая толщина грунта основания характеризуется средним модулем деформации грунта;
- среднее давление под подошвой фундамента не превышает расчетного сопротивления грунта основания.
Далее рассматривают четыре расчетные схемы зданий:
I схема - неравномерная осадка фундамента обусловлена относительно низким значением модуля деформации грунта в торце здания. В вершине трещины (в фундаменте) образован пластический шарнир. Раскрытие трещины носит затухающий характер.
II схема - неравномерная осадка фундамента происходит из-за относительно низкого модуля деформации грунта в средней части здания. Трещина имеет максимальное раскрытие в цоколе здания.
III схема - неравномерная осадка фундамента в торце здания вызвана просадкой грунта или оползнем. Трещина (трещины) отсекает относительно малую часть здания. В вершине трещины образован пластический шарнир.
IV схема (характерна для зданий с ленточным фундаментом из бутового камня) - неравномерная осадка фундамента происходит из-за относительно низкого модуля деформации грунта в торце здания. Трещина рассекает стену и фундамент, образуя своеобразный "деформированный шов".
Расчет стального пояса зданий (I схема)
Рассмотрим напряженно-деформированное состояние здания, деформации которого обусловлены неоднородностью физико-механических характеристик грунтового основания. Предположим, что модуль деформации грунта на участке А-В длиной l1 увеличивается от 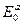 до
до 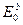 ,а на участке В-С длиной l2 остается постоянным и равным
,а на участке В-С длиной l2 остается постоянным и равным 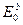 (рис.4.1). Под воздействием реологических процессов с течением времени произойдет перераспределение напряжений под подошвой фундамента. Вследствие этого в кирпичной стене будут нарастать растягивающие напряжения. Если величина растягивающих усилий достигнет предела прочности кирпичной кладки на растяжение, то в стене образуется трещина, которая разделит здание на два блока. Будем считать в дальнейших расчетах, что эти блоки являются абсолютно жестким и деформируются они относительно друг друга в результате поворота вокруг точки В (рис. 4.2).
(рис.4.1). Под воздействием реологических процессов с течением времени произойдет перераспределение напряжений под подошвой фундамента. Вследствие этого в кирпичной стене будут нарастать растягивающие напряжения. Если величина растягивающих усилий достигнет предела прочности кирпичной кладки на растяжение, то в стене образуется трещина, которая разделит здание на два блока. Будем считать в дальнейших расчетах, что эти блоки являются абсолютно жестким и деформируются они относительно друг друга в результате поворота вокруг точки В (рис. 4.2).
При усилении здания стальными тяжами в некоторый момент последние будут исполнять роль дополнительных связей, препятствующих дальнейшим взаимным деформациям блоков здания. Однако с течением времени под воздействием релаксации напряжений грунта на участке А-В будет происходить постепенное перераспределение усилий, а именно: напряжения в точках А и С уменьшается до расчетных величин σa и σc, а напряжения в точке В возрастут до σb (рис.4.3). Усилия в тяжах также будут увеличиваться от 0 до Nт. Будем считать, что напряжения под подошвой фундамента о на участках l1 и l2 меняются по линейному закону.
Запишем условия равновесия здания, усиленного тяжами. Из проекции всех усилий на вертикальную ось получаем
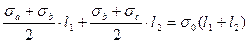 (4.1)
(4.1)
Приравняем нулю моменты, действующие на левый блок, относительно точки В:
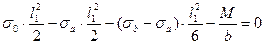 (4.2)
(4.2)
где М = 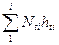 - изгибающий момент, воспринимаемый всеми тяжами;
- изгибающий момент, воспринимаемый всеми тяжами;
b - ширина подошвы фундамента.
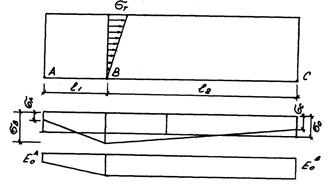
Рис. 4.1. Эпюры распределения напряжений и
модуля деформации основания при отсутствии в стенах трещин
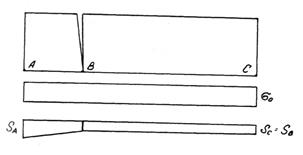
Рис. 4.2. Эпюры распределения напряжений и
осадок основания после образования магистральной трещины
Запишем аналогичное уравнение для правого блока:
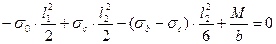 (4.3)
(4.3)
В итоге имеем три уравнения с четырьмя неизвестными. Четвертое уравнение получаем из линейной зависимости деформаций основания в точках А, В и в точке с напряжением σ0:
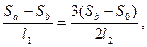 (4.4)
(4.4)
где Sа, Sb, S0 - осадки основания в точках A, Б и в точке с напряжением σ0 за период от t0 до t=∞.
После преобразований уравнений (4.1)-(4.4) получаем систему из четырех линейных уравнений с четырьмя неизвестными σa, σb, σc, М:
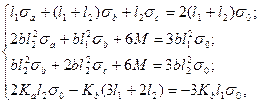 (4.5)
(4.5)
где Кa и Кb - коэффициенты, характеризующие изменение деформационных свойств в точках А и В за период времени от t0 до t = ∞, выделенные из выражения 7,48 [41] и определяемые по формуле
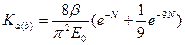 .
.
Коэффициенты, входящие в формулу (4.6), находят из следующих зависимостей:
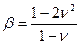 , (4.7)
, (4.7)
где ν - коэффициент бокового расширения грунта;
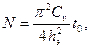 (4.8)
(4.8)
где hэ - высота эквивалентного слоя грунта:
hэ=Awb, (4.9)
здесь Aw - коэффициент эквивалентного слоя грунта;
b - ширина подошвы фундамента.
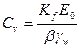 , (4.10)
, (4.10)
где Кf - коэффициент фильтрации;
γw - удельный вес воды.
Решение системы уравнений (4.5) относительно М находим следующим образом:
М = 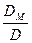 , (4.11)
, (4.11)
где D - определитель системы;
DM - определитель, получающийся из D заменой столбца, составленного из коэффициентов при неизвестном М, столбцом из свободных членов.
После нескольких преобразований окончательно получаем:
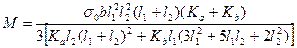 (4.12)
(4.12)
Из уравнения (4.12) следует, что М = 0 тогда, когда Ка-Кb=0 и (или) l1(l2)=0.
Пример 4.1. Требуется рассчитать площадь сечения тяжей стального пояса.
Исходные данные
Здание кирпичное, двухэтажное, длиной 24 м. Магистральная трещина рассекает продольную стену на два блока. Длина блоков l1 = 6м, l2 = 18м (рис.4.4). Продольные стены опираются на ленточные фундаменты шириной b = 1 м. Реактивный отпор грунта в основании фундаментов до момента установки тяжей σ0 = 150 кПА. Грунт - однородная мягкопластичная глина: 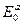 = 16 МПа,
= 16 МПа, 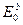 = 20 МПа, Кf = 5·10-10 м/с, ν = 0,4.
= 20 МПа, Кf = 5·10-10 м/с, ν = 0,4.
Стальной пояс устанавливается через 1 год после образования трещины: t0 = 3,15·107 с.
Неравномерная осадка основания вызвана незаконченной фильтрационной консолидацией грунта.
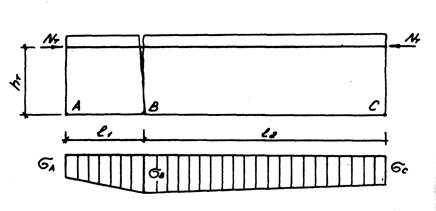
Рис.4.3. Схема расчетных усилий (напряжений) здания,
усиленного стальным поясом
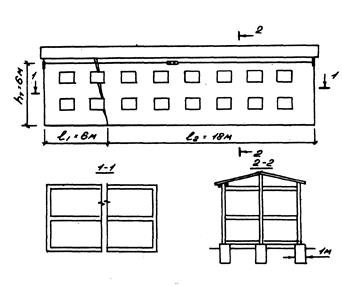
Рис.4.4. Эскиз усиления кирпичной стены стальным поясом поверху
Решение
Находим коэффициенты эквивалентного слоя грунта, используя табличные значения [42, табл. 5.6]:
- для первого блока при 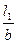 = 6
= 6 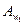 =4,0;
=4,0;
- для второго блока при 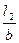 = 18 > 10
= 18 > 10 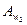 =4,58.
=4,58.
Находим высоту эквивалентного слоя грунта по формуле (4.9):
hэ1= 4·1=4 м; hэ2= 4,58·1=4,58 м.
Используя формулы (4.6)-(4.9), находим следующие коэффициенты:
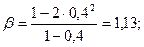
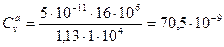 м2/с;
м2/с;
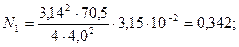
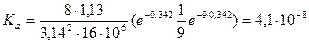 м2/Н;
м2/Н;
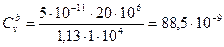 м2/с;
м2/с;
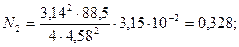
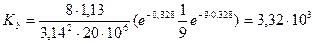 Нм.
Нм.
Изгибающий момент, воспринимаемый тяжами, устанавливаемыми на стену, определяем по формуле (4.12)
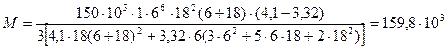 Нм
Нм
Усилие в тяжах, устанавливаемых на высоте hт = 6 м, равно
NТ= 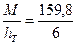 = 26,23 кН.
= 26,23 кН.
Требуемая площадь сечения определяется по формуле (при Rs=210 МПа)
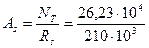 = 1,27 см2.
= 1,27 см2.
Принимаем два тяжа Ø12, Аs = 2,26 см2. Эскиз усиления стены поясом представлен на рис.4.4.
Расчет стального пояса зданий (II схема)
Неравномерная осадка фундаментов обусловлена неоднородностью основания. При этом модуль деформации грунта имеет минимальную величину в средней части здания, а образовавшиеся в стенах трещины получают наибольшее раскрытие в цоколе (рис.4.5).
Базируясь на расчетных предпосылках, изложенных в первой расчетной схеме, сформулируем условия равновесия здания, усиленного тяжами, расположенными в цоколе здания (рис.4.6).
Из проекции всех усилий на вертикальную ось получаем
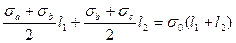 . (4.13)
. (4.13)
Приравниваем нулю моменты, действующие на левый блок относительно точки В.
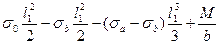 = 0, (4.14)
= 0, (4.14)
г
где М = 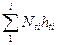 - изгибающий момент, воспринимаемый всеми тяжами;
- изгибающий момент, воспринимаемый всеми тяжами;
b - ширина подошвы фундамента.
Аналогичное уравнение для правого блока выглядит следующим образом:
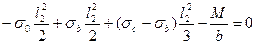 (4.15)
(4.15)
В итоге располагаем тремя уравнениями с четырьмя неизвестными. Четвертое уравнение получаем из линейной зависимости деформаций основания в точках А, В и С:
(Sa-Sb)(l2+l1) = (Sb-Sa)(l2-l1). (4.16)
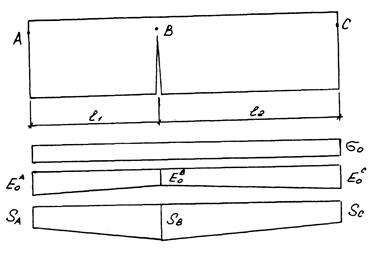
Рис.4.5. Эпюры распределения напряжений и осадок основания
после образования магистральной трещины
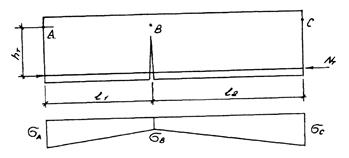
Рис.4.6. Схема усилий (напряжений) для здания усиленного стальным поясом
После преобразований уравнений (4.13)-(4.1б) получаем систему из четырех линейных уравнений с четырьмя неизвестными σa, σb, σc, М:
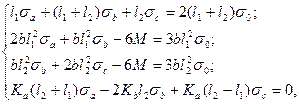 (4.17)
(4.17)
где Ка и Kb - коэффициенты, характеризующие изменение деформационных свойств грунта в точках А и В за 1 период времени от t0 до ∞ и определяемые по формуле (4.6).
Из решения системы уравнений (4.17) получаем формулу для определения изгибающего момента в следующем виде:
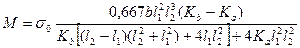 (4.18)|
(4.18)|
Пример 4.2. Требуется рассчитать площадь сечения тяжей стального пояса.
Исходные данные
Здание кирпичное, двухэтажное, длиной 22 м. Высота этажа; 2,8 м. Несущие стены продольные на ленточном фундаменте шириной b = 1 м. Магистральная трещина, рассекающая продольную стену на два блока, доходит до окон второго этажа. Длина блоков l1 = 10 м, l2 = 12 м (рис.4.7). Реактивный отпор грунта до момента установки пояса σ0 = 180 кПа. Стальной пояс устанавливается через 6 месяцев после образования трещины t0 = 1,58·107 с.
Грунт - однородная глина 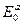 = 20 МПа,
= 20 МПа, 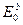 = 16 МПа, Kf = 5·10-10 м/с, ν=0,4.
= 16 МПа, Kf = 5·10-10 м/с, ν=0,4.
Коэффициенты эквивалентного слоя грунта обоих блоков [42, табл.5.6] приняты Аw = 4,58.
Решение
Находим высоту эквивалентного слоя грунта по формуле
hэ = Aw·b = 4,58·1 = 4,58 м.
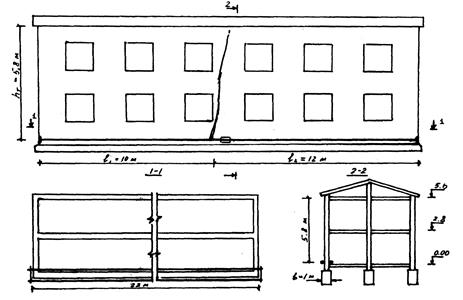
Рис. 4.7. Эскиз усиления стены стальным поясом понизу
Используя формулы (4.6)-(4.9), находим коэффициенты:
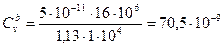 м2/с;
м2/с;
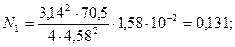
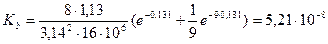 м2/Н;
м2/Н;
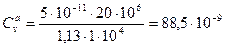 м2/с;
м2/с;
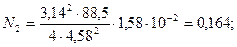
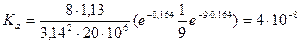 м2/Н.
м2/Н.
Находим изгибающий момент, воспринимаемый тяжами, устанавливаемыми на одну стену, по формуле (4.18):
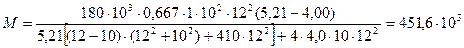 Нм.
Нм.
Тяжи, воспринимающие растягивающие усилия, располагаем в уровне пола первого этажа. Принимая во внимание картину трещинообразования, будем считать, что в кирпичной кладке, расположенной выше верха окон второго этажа, действуют сжимающие напряжения. Тогда плечо hT действия усилия в тяжах относительно центра тяжести сжатой зоны можно принять равным 55,8 м.
Усилие в тяжах составит:
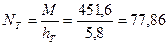 кН
кН
Требуемая площадь сечения тяжей при Rs = 210 МПа равна:
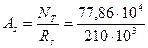 = 3,71 см.
= 3,71 см.
Принимаем два тяжа диаметром 16 мм с площадью сечения Аs = 4,02см2. Эскиз усиления стены поясом представлен на рис.4.7.
Расчет стального пояса зданий (III схема)
Большие быстро прогрессирующие деформации грунта основания (от просадки или оползня) под торцом здания, приводят к образованию магистральной трещины в несущих стенах. При этом ширина раскрытия трещины быстро увеличивается, грозя обрушением здания. Предотвратить это можно с помощью стального пояса (поясов), удерживающего оторванный блок здания от углового перемещения (рис.4.8).
В зданиях с монолитным ленточным железобетонным фундаментом поворот блока происходит относительно точки В, расположенной в уровне центра тяжести сжатой арматуры, фундамента.
Если не учитывать реактивный отпор грунта в зоне просадки, то усилие в поясе можно определить из условия равновесия моментов относительно точки В при 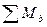 = 0:
= 0:
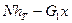 = 0, (4.19)
= 0, (4.19)
где G2 - масса оторванного блока здания.
Применимость формулы ограничивается условием G2/G1≥3.
Пример 4.3. Требуется рассчитать площадь сечения тяжей стального пояса.
Исходные данные
Здание кирпичное, одноэтажное. Фундамент ленточный железобетонный. Кирпичные стены толщиной δ = 0,51 м выполнены из обыкновенного красного кирпича марки 75 на растворе марки 50 (Rsq = 0,112 МПа). В результате просадки основания произошел отрыв части здания массой G1 = 350 кН, длиной l1 = 3 м. В вершине трещины (в фундаменте) образовался пластический шарнир. Стальной пояс монтируется в уровне перекрытия на высоте hт = 4,2 м (см. рис.4.8). Общая масса здания G1=G2=1800 кН.
Решение
Проверяем условие
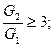
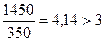
Находим требуемое усилие в поясе (см. рис.4.8):
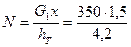 = 125 кН
= 125 кН
Расчетная площадь сечения тяжей из ст.3 (Rs = 210 МПа):
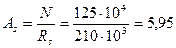 см2.
см2.
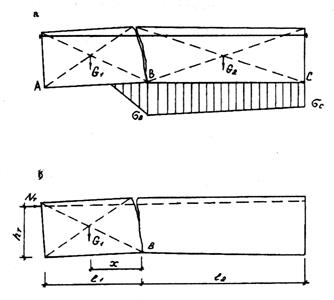
Рис.4.8. Расчетная схема усиливаемого здания при просадке грунта:
а - эпюра реактивного отпора грунта; б - расчетная схема
Принимаем два тяжа Ø20 общей площадью сечения As = 6,28 см2. Проверяем прочность кладки на срез по неперевязанному шву:
N ≤ (Rsg + 0,8nμσ0)А
В соответствии с п. 4.20 СНиП П-22-81 принимаем коэффициенты n = 1, μ = 0,7. Среднее напряжение в кладке на уровне стального пояса принимаем σ0 = 0,04 МПа.
Суммарная площадь сечения кладки в плоскости среза при двух продольных и одной торцевой стене равна: A=3·0,51·2+6·0,51 = 6,12 м2.
Проверяем условие прочности:
125 кН < (0,112 + 0,8·1,0·0,7·0,04)·103·6,12 = 808 кН.
Условие выполняется.
Проектируя усиление стальным поясом, необходимо предусматривать конструктивные мероприятия, препятствующие образованию горизонтальных трещин в стенах, в зоне просадки грунта. Для этой цели можно использовать стальной корсет из вертикальных и горизонтальных стержней, образующих замкнутый контур.
Расчет стального пояса зданий (IV схема)
Четвертый вариант расчетной схемы отличается от ранее рассмотренных тем, что трещина рассекает не только стены здания, но также и фундамент. Отсекаемые трещиной части здания взаимно смещаются. Прекращение роста или частичное закрытие трещины происходит от усилия натяжения пояса и обусловленного им перераспределения напряжений в основании деформируемого блока.
Усилие в поясе определяется из условия равновесия моментов относительно точки О (рис.4.9) при 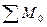 = 0:
= 0:
NhT-Pfh/6=0, (4.20)
где Рf - равнодействующая фиктивного отпора грунта, при котором деформации основания блока выравниваются:
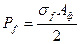 (4.21)
(4.21)
здесь σf - напряжение фиктивного отпора грунта, необходимое для выравнивания деформаций основания:
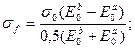 (4.22)
(4.22)
σ0 - реактивный отпор грунта до усиления:
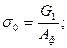 ; (4.23)
; (4.23)
G1 - масса усиливаемого блока;
Aф - суммарная площадь фундамента под блоком.
Пример 4.4. Требуется рассчитать площадь сечения тяжей стального пояса.
Исходные данные
Здание кирпичное, трехэтажное. Конструкция и материал кирпичных стен аналогичны представленным в примере 4.3. Фундамент ленточный бутовый с шириной подошвы b = 1 м.
В результате неравномерной осадки фундамента произошел отрыв блока здания длиной l = 5 м. Трещина шириной 3 см разрезает продольные стены и ленточный фундамент. Стальной пояс устанавливается в уровне перекрытия 3-го этажа относительно подошвы фундамента на высоте hт = 7 м. Грунт основания - глина; 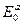 = 21 МПа;
= 21 МПа; 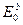 = 24 МПа. Реактивный отпор грунта до усиления поясом σ0 = 0,2 МПа.
= 24 МПа. Реактивный отпор грунта до усиления поясом σ0 = 0,2 МПа.
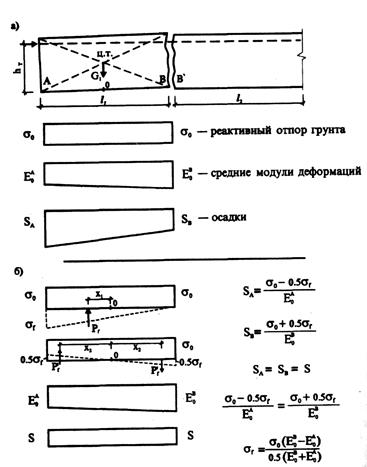
Рис.4.9. Расчетная схема усиливаемого здания
при сквозной трещине, разрезающей стены и фундамент:
а - до усиления; б - после усиления
Решение
Пользуясь формулой (4.22), определяем фиктивный отпор грунта, который бы способствовал выравниванию осадок в точках А и В:
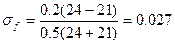 МПа
МПа
Суммарная площадь подошвы фундамента оторванного блока
Аф = 5·2·1 + 6·1 = 16 м2.
Находим равнодействующую фиктивного отпора грунта по формуле (4.21):
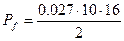 = 216 кН
= 216 кН
Пользуясь расчетной схемой (рис.4.9), находим требуемое усилие натяжения пояса:
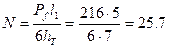 кН
кН
Задаемся усилием натяжения тяжей N = 0,3RsAs.
Требуемая площадь сечения тяжей из Ст3 (Rs = 210 МПа):
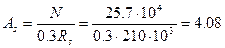 = 4.08 см2
= 4.08 см2
Принимаем два тяжа Ø18, Аs = 5,09 см2.
Прочность кирпичной кладки стены на срез не проверяем, так как при прочих равных условиях с учетом данных примера 4.3 площадь среза стены выше, а усилие в тяжах ниже. Следовательно, условие прочности выполняется.
Методика расчета поясов оптимального сечения
Проектирование стальных поясов, устанавливаемых для усиления здания, является многовариантной задачей. Практика показывает, что разработанное даже опытным проектировщиком конструктивное решение не всегда является экономичным.
Рассмотрим задачу оптимального проектирования пояса, где учитываются требования минимального расхода стали с позиций прочности как самого пояса, так и прочности на срез каменной кладки усиливаемого объекта. В общем случае задача оптимизации сводится к отысканию экстремума целевой функции
c(x1, х2,..., xn) = min(mах),
где xi - определяющие параметры конструкции.
При этом должны выполняться ограничения в виде системы неравенств, представляющие собой требования действующих норм. Исходя из этого запишем целевую функцию в следующем виде:
с = СсA(l1+l2)γn,
где с - общая стоимость стальных поясов;
Сс - стоимость единицы массы стальных поясов;
А - площадь поперечного сечения одного стального пояса;
n - количество поясов;
γ - плотность стали.
Систему ограничений выразим в виде двух неравенств. Первое, неравенство представляет собой условие прочности стальных поясов
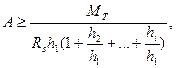
где Мт - момент, воспринимаемый стальными поясами, определяемый по формулам (4.6) или (4.16);
Rs - расчетное сопротивление стали;
hi - плечо усилия, воспринимаемого i-тым поясом.
Второе неравенство представляет собой условие прочности кирпичной кладки на срез:
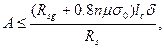
где Rsg - расчетное сопротивление кладки на срез;
lс - длина срезаемой части кирпичной кладки;
δ - толщина стены;
n, μ - коэффициенты, принимаемые в соответствии с 4.20 СНиП П-22-81.
На рис.4.10 представлена блок-схема оптимизации стальных поясов.
Необходимо подчеркнуть, что рассмотренные методы расчета стальных поясов являются достаточно приближенными и могут использоваться в коротких зданиях малой этажности (1-3 этажа) с жесткой конструктивной схемой. При значительной протяженности здания (более 30 м) рассчитывать усиленные поясом стены следует по схеме балки переменного сечения на упругом основании, однако структура расчетных формул в этом случае существенно усложняется.
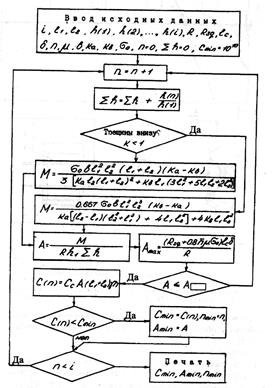
Рис. 4.10. Блок-схема расчета поясов оптимального сечения
