Задания и порядок выполнения работы.

1. Изучить теорию работы, разобраться в устройстве лабораторно­го стенда и методике измерений.

2. Генератор ГЗ-106 подключить к лабораторному стенду, включить и настроить на частоту выходного сигнала 10 кГц с амплитудой примерно 1 В.

3. Изменяя емкость переменного конденсатора колебательного контура , добиться резонанса в контуре (наблюдая на осциллографе резонанс напряжений в . контуре). При этом собственная частота колебаний в контуре окажется равной частоте внешнего сигнала, т. е. 10 кГц.

4. Изменяя частоту генератора ГЗ-106 в диапазоне от 5 до 15 кГц, снять резонансные кривые для исследуемого контура при различных значениях активного сопротивления R.

6. С помощью осциллографа намерить амплитудные значения напряжений в контуре при резонансе. Вычислить индуктивность контура из формулы Томсона 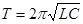, взяв емкость конденсатора
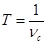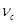по шкале стенда и учитывая, что где - собственная частота
контура.

6. Построить на графике резонансные кривые и определить по ним полосу пропускания контура в различных режимах. Рассчитать доброт­ность контура по формуле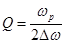

7. Рассчитать волновое сопротивление контура по формуле

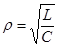
Лабораторная работа № 12а

ИЗУЧЕНИЕ СВОБОДНЫХ КОЛЕБАНИЯ В ЭЛЕКТРИЧЕСКОМ КОНТУРЕ

Цель работы: изучение свободных колебаний в электрическом кон­туре и определение параметров контура.

Колебаниями называются процессы, характеризующиеся повторяемо­стью во времени. Свойством повторяемости обладают, например, качания маятника, колебания струны или ножек камертона, изменение напряжения на обкладках конденсатора в колебательном контуре и т. д. Одним ив основных параметров колебательного процесса является его период Т, т. е. время, спустя которое система возвращается в исходное состояние. Другим важным параметром колебательного процесса является частота колебаний, т. е. количество колебаний, совершаемых в единицу времени. Частоту колебаний обычно обозначают греческой буквой ν и очевидно, что частота ν связана с периодом Т соотношением:

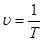⁽¹⁾

Свободными или собственными называются такие колебания, которые происходят в системе, предоставленной самой себе после выведения ее из состояния равновесия.

1. Электрический колебательный контур

Рассмотрим колебательный контур, представляющий собой электри­ческую цепь, состоящую из последовательно соединенных конденсатора С, катушки индуктивности L и проводника с омическим сопротив­лением R (рис. 1). Ток, текущий в колебательном контуре, считает­ся квазистационарным, когда мгновенные значения тока практически одинаковы на всех участках проводов, а изменения силы тока во времени происходят достаточно медленно, чтобы распространение элект­родинамических взаимодействий в цепи можно было считать мгновен­ным. Для мгновенных значений параметров квазистационарных токов справедливы закон Ома, правила Кирхгофа и т. д., установленные для цепей постоянного тока. Обозначим через С- заряд на обкладках кон­денсатора в данный момент времени, Ή - разность потенциалов на его пластинах 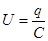, где С - емкость конденсатора. Условимся считать положительным ток I .заряжающий конденсатор, тогда 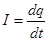t - время. Воспользуемся 2-ым законом Кирхгофа ( законом Ома для неоднород­ного участка цепи ), согласно которому сумма падений напряжений в замкнутом контуре равна сумме имеющихся в конту­ре ЭДС. В рассматриваемом контуре действует ЭДС . самоиндукции 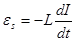возникающая в катушке индуктивности при изменении силы тока. Следовательно, уравнение Кирхгофа для колебательного 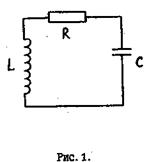контура имеет вид:

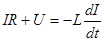
(2)

или с учетом того, что 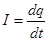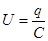и разделив (2) на L, полу­чим:

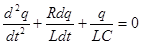
(3)

Это уравнение позволяет описать динамику изменения заряда конденсатора в рассматриваемом контуре в отсутствие внешней ЭДС.