Методические указания по выполнению лабораторных работ
См. приложение 1
МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ВЫПОЛНЕНИЮ ПРАКТИЧЕСКИХ РАБОТ
Практическая работа №1
Построение асимптотических ЛАЧХ и временных характеристик элементарных динамических звеньев.
Задание
1. Рассмотреть ЛАЧХ для апериодического и интегрирующего звеньев .
Частотные характеристики систем САУ
Частотные характеристики САУ характеризуют реакцию систем на синусоидальное входное воздействие в установившемся режиме.
К частотным характеристикам относятся:
АФЧХ - амплитудно-фазовая частотная характеристика;
АЧХ – амплитудно-частотная характеристика;
ФЧХ – фазовая частотная характеристика;
ЛАЧХ – логарифмическая АЧХ;
ЛФЧХ – логарифмическая ФЧХ.
АФЧХ представляет собой частотную передаточную функцию W(jω), которая получается путем замены в передаточной функции W(p) оператора Лапласа p на комплексную переменную jω. АФЧХ представляет собой вектор на комплексной плоскости в полярных координатах Н(ω) и φ(ω), которые являются соответственно АЧХ и ФЧХ:
W(jω) = Н(ω)∙еjφ(ω) = N(ω) + jM(ω). (1)
Здесь: Н(ω) – АЧХ, которая представляет собой зависимость значения модуля вектора АФЧХ от круговой частоты;
φ(ω) – ФЧХ, которая представляет собой зависимость аргумента вектора АФЧХ от круговой частоты;
N(ω) = Н(ω)∙cosφ(ω) – проекция вектора АФЧХ на действительную ось комплексной плоскости;
M(ω) = Н(ω)∙sinφ(ω) – проекция вектора АФЧХ на мнимую ось комплексной плоскости;
При изменении частоты ω от нуля до бесконечности АФЧХ представляет собой кривую в комплексной плоскости, называемую годографом.
Рассмотрим частотные характеристики отдельных типовых звеньев.
Апериодическое звено.
Основные формулы и соотношения
W(jω) = K/(1 + jωT) = 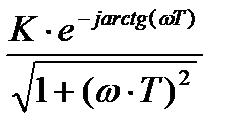 =
= 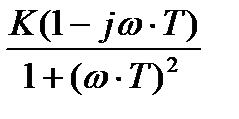 .
.
Н(ω) = 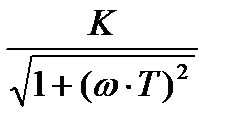 ; φ(ω) = – arctg(ωT);
; φ(ω) = – arctg(ωT);
N(ω) = K/[1 + (ω∙T)2]; M(ω) = – K∙ ω∙T/[1 + (ω∙T)2]. (2)
φ(0) = 0o; Н(0) = K; N(0) = K; M(0) = 0;
φ(ω = 1/T) = – 45o; Н(T) = K/√2; N(T) = K/2; M(T) = – K/2;
φ(ω → ∞) = – 90o; Н(∞) = N(∞) = M(∞) = 0.
Интегрирующее звено.
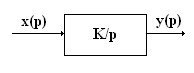
Основные формулы и соотношения
W(jω) = K/jω = K∙e 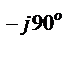 /ω;
/ω;
Н(ω) = K/ω; φ(ω) = – 90o;
N(ω) = 0; M(ω) = – K/ω; (3)
φ(0) = – 90o; Н(0) = ∞; N(0) = 0; M(0) = – ∞;
φ(ω → ∞) = – 90o; Н(∞) = N(∞) = M(∞) = 0.
Практическая работа №2
Расчет устойчивости линейных САУ с использованием алгебраических критериев.
Задание
1. Определить необходимое и достаточное условие устойчивости САУ
Устойчивость линейных систем САУ
САУ называется устойчивой, если с течением времени выходная величина стремится к установившемуся значению при постоянном значении входного сигнала. Линейная САУ называется неустойчивой, если выходная величина неограниченно возрастает с течением времени.
Динамика линейных САУ, как отмечалось нами ранее, описывается линейным дифференциальным уравнением с постоянными вещественными коэффициентами:
an∙y(n) + a(n-1)∙y(n-1) + ∙∙∙ + a0∙y = bm∙x(m) + b(m-1)∙x(m-1) + ∙∙∙ + b0∙x (1)
Равенство (1) выводится из уравнений отдельных звеньев, образующих систему САУ. Параметры же переходного процесса в САУ определяются решением однородного дифференциального уравнения, получаемого путем приравнивания левой части равенства (1) нулю:
an∙y(n) + a(n-1)∙y(n-1) + ∙∙∙ + a0∙y = 0 (2)
Решение данного уравнения имеет вид: y(t) = 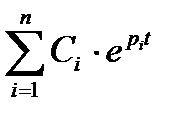 , (3)
, (3)
где Ci – постоянные интегрирования;
pi – корни характеристического уравнения, получаемого путем замены в уравнении (2) знака дифференцирования на оператор Лапласа р:
an∙р(n) + a(n-1)∙р(n-1) + ∙∙∙ + a0 = 0 (4)
Как видим, выражение (3) представляет собой сумму экспоненциальных функций. Система будет устойчивой, если выполняется условие:
y(t) → 0, при t → ∞.
Это условие будет выполнено только в одном случае, если все экспоненты в правой части равенства (3) будут стремиться к нулю. А любая экспоненциальная функция от времени будет стремиться к нулю, если показатель ее степени будет отрицательным числом. Отсюда можно сделать следующие выводы. Система САУ будет устойчива, если:
1) все корни pi характеристического уравнения являются действительными отрицательными числами (pi< 0);
2) если имеется пара комплексных и сопряженных корней типа pi,i+1 = α +_ jβ, то в равенство (3) входят слагаемые:
Cie(α + jβ)t + Ci+1e(α - jβ)t = Cieαt∙ejβt + Ci+1eαt∙e –jβt =
= Cieαt∙[cos(βt) + jsin(βt)] + Ci+1eαt∙[cos(βt) - jsin(βt)].
Поэтому при α< 0 и Ci = Ci+1 в график функции y(t) данные слагаемые входят как затухающие по амплитуде косинусоидальные составляющие.
Следовательно, необходимым и достаточным условием устойчивости САУ является наличие отрицательного знака действительной части корней характеристического уравнения. Впервые это условие для механических систем сформулировал и доказал русский ученый А.М. Ляпунов.
При наличии, хотя бы одного корня с положительной действительной частью график функции y(t) будет представлять собой возрастающую экспоненту или косинусоиду, и процесс регулирования будет неустойчивым.
Если хотя бы один из корней (pi= 0), то функция y(t) будет содержать постоянную составляющую Ciepit = Ci, что соответствует нахождению САУ на грани устойчивости. В аналогичном состоянии будет находиться система в случае наличия чисто мнимых корней характеристического уравнения.
Рассмотренное условие устойчивости относится к линейным САУ. Но практически все реальные САУ являются нелинейными и только приближенно многие из них можно описать линейными уравнениями. Так, например, Ляпунов доказал, что по устойчивости линеаризованной системы можно судить об устойчивости исходной нелинейной системы.
ЗАДАНИЕ НА КОНТРОЛЬНЫЕ РАБОТЫ И МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ИХ ВЫПОЛНЕНИЮ
КОНТРОЛЬНАЯ РАБОТА №1
ОБЩИЕ УКАЗАНИЯ
Для успешного выполнения контрольной работы студент должен иметь представление об основных формах записи линейных дифференциальных уравнений, передаточных функций, временных и частотных характеристик элементарных динамических звеньев систем автоматического управления (САУ), а также ознакомится с основными понятиями и определениями теории автоматического управления. Прежде, чем приступить к выполнению контрольной работы студент должен изучить соответствующие разделы основной [1 и 2] и рекомендованной литературы [3].
Цель контрольной работы – закрепить знания, полученные студентом при самостоятельном изучении дисциплины.
Необходимые чертежи и графики выполняются карандашом на белой бумаге стандартных размеров: 297х210 мм. Пояснительная записка пишется от руки или машинописно на одной стороне стандартного листа аналогичного формата. Все листы записки, в том числе графики и таблицы, должны быть сброшюрованы и иметь сплошную нумерацию, показанную в правом верхнем углу каждого листа. Для замечаний рецензента слева оставляют поля шириной 4 см. Исправления по замечаниям делаются на чистой стороне листа рядом с замечаниями рецензента, которые нельзя удалять, и сопровождают надписью «Работа над ошибками».
Контрольная работа содержит задание, состоящее из трех задач. Пояснительная записка должна содержать условия и исходные данные к каждой задаче согласно своему варианту. Ход решения задачи должен сопровождаться краткими пояснениями с приложением необходимых таблиц с расчетными данными и графиков. Под графиками должно стоять конкретное его наименование, оси координат должны быть промасштабированы и обозначены с указанием принятой размерности функции и аргумента. Все чертежи с графиками вставляются в пояснительную записку сразу после той страницы, на которой имеется первая ссылка на него. Все пояснения выполненной работы, а также приводимые формулы должны быть разборчивыми для чтения. Сокращения слов в тексте, кроме общепринятых, не допускается. Также не допускается ксерокопирование текста, графиков или рисунков.
В конце пояснительной записки рекомендуется приводить список использованной литературы.
ЗАДАНИЕ НА КОНТРОЛЬНУЮ РАБОТУ
