Описание алгоритма (метода анализа)

Описание исходных данных

В качестве исходного массива данных были выбраны данные «Iris»

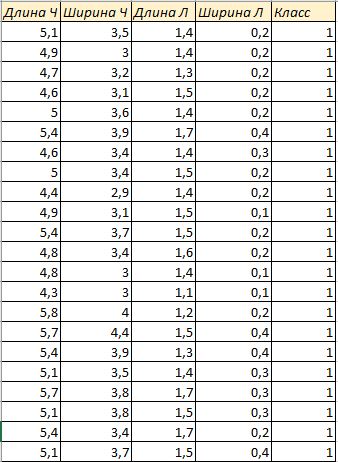
Рис.1. Фрагмент таблицы исходных данных

Общее количество данных: 150

Пропущенные значения: нет

Выбросы: нет

Количество атрибутов: 5 (длина и ширина чашелистика, длина и ширина лепестка в сантиметрах, класс [1 – Iris Setosa, 2 – Iris Versicolour, 3 – Iris Virginica])

Описательная статистика

Описательная статистика применяется для создания одномерного статистического отчета, содержащего информацию о центральной тенденции и изменчивости входных данных.

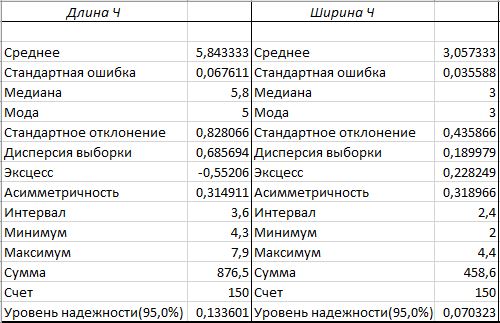
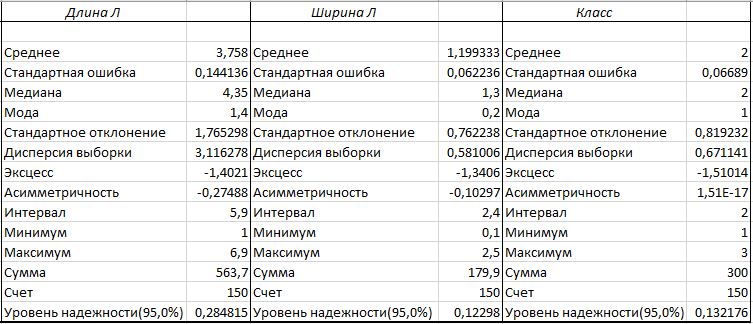
Рис.2. Описательная статистика

Эксцесс показывает «остроту пика» распределения, характеризует остроконечность или сглаженность распределения по сравнению с нормальным распределением. Положительный эксцесс обозначает относительно остроконечное распределение, а отрицательный – относительно сглаженное распределение. Эксцесс нормального распределения равен нулю. Асимметричность показывает отклонение распределения от симметричного. Если асимметрия существенно отличается от нуля, то распределение несимметрично, нормальное распределение абсолютно симметрично. Так как эксцесс и асимметричность близка к нулю, то можно сделать вывод о том, что распределение близко в нормальному.

Описание алгоритма (метода анализа)

3.1 Дисперсионный анализ

Дисперсионный анализ применяется для исследования влияния одной или нескольких качественных переменных (факторов) на одну зависимую количественную переменную. Сущность дисперсионного анализа заключается в расчленении общей дисперсии изучаемого признака на отдельные компоненты, обусловленные влиянием конкретных факторов, и проверке гипотез о значимости влияния этих факторов на исследуемый признак. Сравнивая компоненты дисперсии друг с другом посредством F-критерия Фишера, можно определить, какая доля общей вариативности результативного признака обусловлена действием регулируемых факторов. Дисперсионный анализ относится к группе параметрических методов и поэтому его следует применять только тогда, когда доказано, что распределение является нормальным.

В лабораторной работе использовался однофакторный дисперсионный анализ, при котором изучается действие только одной переменной (фактора) на исследуемый признак.

3.2 Корреляционный анализ

Корреляционный анализ используется для количественной оценки взаимосвязи двух наборов данных, представленных в безразмерном виде. Если большие значения из одного набора данных связаны с большими значениями другого набора, то корреляция положительна, если малые значения одного набора связаны с большими значениями другого, то корреляция отрицательна, если данные двух диапазонов никак не связаны между собой, корреляция близка к нулю.

Ковариационный анализ, аналогично корреляционному, используется для вычисления среднего произведения отклонений точек данных от относительных средних. Ковариация является мерой связи между двумя диапазонами данных.

3.3 Регрессионный анализ

Это группа методов, направленных на выявление и математическое выражение тех изменений и зависимостей, которые имеют место в системе случайных величин. Линейный регрессионный анализ заключается в подборе графика для набора наблюдений с помощью метода наименьших квадратов.

Регрессионный анализ позволяет установить функциональную зависимость между некоторой случайной величиной Y и некоторыми, влияющими на Y, величинами X. Такая зависимость получила название уравнения регрессии. Для оценки степени связи между величинами используется коэффициент множественной корреляции R Пирсона, который может принимать значения от 0 до 1. R=0, если между величинами нет никакой связи, и R=1, если между величинами имеется функциональная связь. Величина R2 называется коэффициентом детерминации и характеризует качество полученной регрессионной прямой. Это качество выражается степенью соответствия между исходными данными и регрессионной моделью.

Контрольный пример

4.1 Дисперсионный анализ

Однофакторный дисперсионный анализ позволяет проверить гипотезу 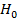: длина чашелистика не влияет на длину лепестка.

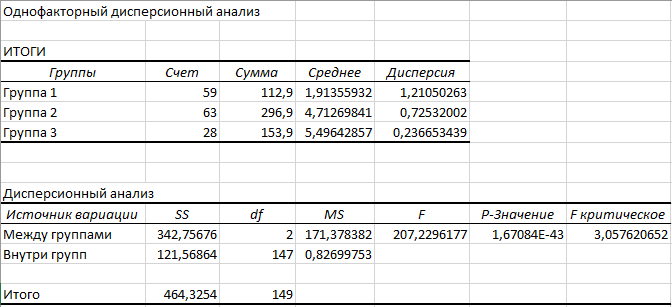
Рис.3. Однофакторный дисперсионный анализ зависимости класса цветка от длины чашелистика

Значение F > F критическое, поэтому можно утверждать, что различия между группами данных носят неслучайный характер, то есть на уровне значимости 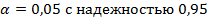гипотеза 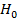отвергается и принимается альтернативная гипотеза: длина чашелистика влияет на длину лепестка цветка.

4.2 Корреляционный анализ

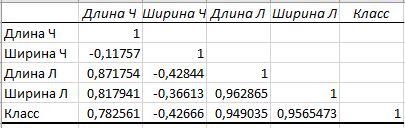
Рис.4. Результаты корреляционного анализа

Степень корреляции варьируется в пределах 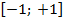. Если степень равна нулю, то связь между параметрами отсутствует. Если степень положительна, то зависимость прямая. А если степень отрицательна, то зависимость обратная.

Получив результаты, можно сказать, что корреляция между длиной чашелистика и шириной чашелистика равна -0,12 (слабая обратная взаимосвязь). Корреляция между длиной чашелистика и длиной лепестка равна 0,87 (сильная взаимосвязь). Корреляция между длиной чашелистика и шириной лепестка равна 0,82 (сильная взаимосвязь). Корреляция между длиной чашелистика и классом цветка равна 0,78 (достаточно сильная взаимосвязь). Между шириной чашелистика и длиной лепестка корреляция равна -0,43 (умеренная обратная взаимосвязь). Между шириной чашелистика и шириной лепестка равна -0,37 (слабая обратная взаимосвязь). Между шириной чашелистика и классом цветка равна -0,43 (умеренная обратная взаимосвязь). Корреляция между длиной лепестка и шириной лепестка равна 0,96 (очень сильная взаимосвязь). Между длиной лепестка и классом цветка равна 0, 95 (очень сильная взаимосвязь). И, наконец, между шириной лепестка и классом цветка корреляция равна 0,96 (также очень сильная взаимосвязь).

4.3 Регрессионный анализ

Построим линейную регрессионную модель Y=Y(X),где Y – длина чашелистика, X – длина лепестка.

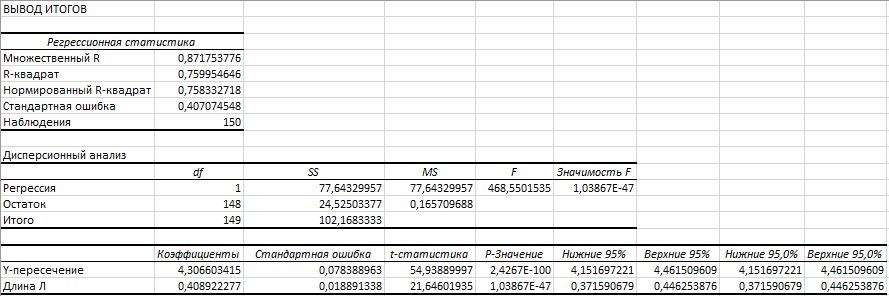
Рис.5. Результаты регрессионного анализа

R-квадрат демонстрирует то, что на 76% (при 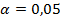) расчетные параметры модели объясняют зависимость и изменения параметра Y от факторов X. Модель является линейной и имеет вид: Y=0,4 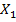+4,3.

4.4 Гистограмма остатков

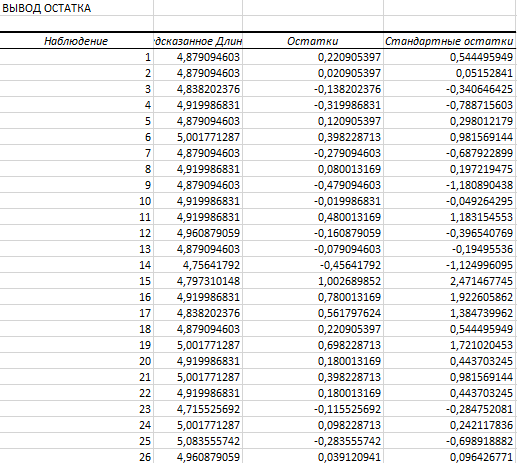
Рис.6. Фрагмент таблицы остатков

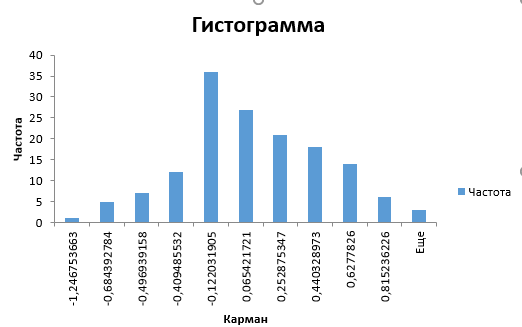
Рис.7. Гистограмма остатков

Распределение остатков отличается от нормального распределения, но определенная мера сходства с ним присутствует.

4.5 Скользящее среднее

Скользящее среднее показывает усредненное значение длины чашелистика и позволяет сделать прогноз на то, какие значения примет функция.

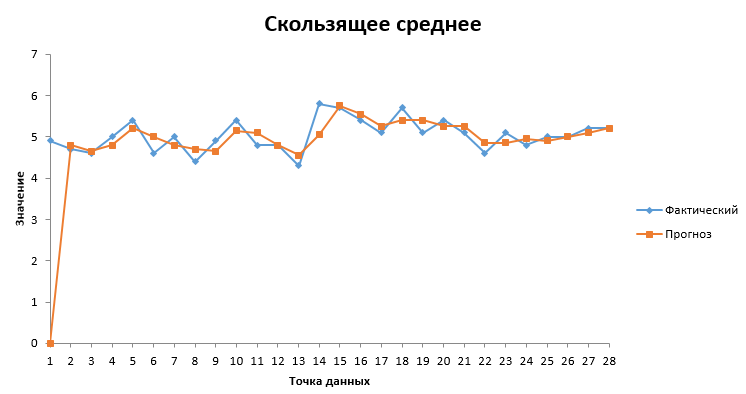
Рис.8. Скользящее среднее

Выводы:

В ходе лабораторной работы произошло ознакомление с теорией дисперсионного, корреляционного и регрессионного анализов, а также были получены практические навыки и умения выполнения вышеперечисленных анализов в среде MS Excel с помощью надстройки «Пакет анализа».