ДОДАТОК 1. Про позначення, що вживаються у роздруківках підпрограм з регресійного аналізу пакету статистичних програм STATGRAPHICS.

Наведемо роз’яснення щодо основного змісту роздруківок до рекомендованих лабораторних робіт, які можна одержати за допомогою пакету статистичних програм STATGRAPHICS.

1.Роздруківка Simple Regression.

1.1. Таблиця Regression Analysis – Linear model.

Дана таблиця має наступний вигляд:

Dependent variable: Independent variable:
Parameter	Estimate	Standard Error	T - Statistic	P-value
Intercept Slope
Slope

Перший рядок містить позначення залежної та незалежної змінної. Другий рядок містить назви, що роз’яснюють зміст числових даних третього рядка. Останні є результатами обчислень, що виконані відповідною підпрограмою пакету. Так, у першому стовпчику під рубрикою Parameter містяться назви параметрів, що оцінюються. Це — вільний член α (Intercept) та кутовий коефіцієнт β (Slope) моделі y = α + β x. Їх оцінки у розглядуваній роздруківці позначаються a та b відповідно. Значення a та b наводяться у другому стовпчику під рубрикою Estimate. У третьому стовпчику під рубрикою Standard Error наводяться оцінки середньоквадратичних відхилень величин a та b. Для їх обчислень використовуються рівності (4.17). А саме, беруться корені з величин у правих частинах вказаних рівностей (в останніх замість позначень a, b використовуються, відповідно b₀ та b₁). Четвертий стовпчик під рубрикою T - Statistic містить значення статистик Стьюдента (4.18), (4.19), в яких в якості значень β₀ та β₁ береться число 0. Таким чином, в даному стовпчику наводяться дані для перевірки гіпотез 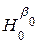: β₀ = 0 та 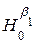: β₁ = 0. Позитивна відповідь при перевірці першої гіпотези означає, що лінію регресії можна вважати такою, що проходить через початок координат. Позитивна відповідь при перевірці другої гіпотези означає, що, по суті, зміна значень незалежної змінної не впливає на значення залежної змінної. Ця гіпотеза має назву гіпотези про незначущість коефіцієнту регресії β₁ (або незначущість регресії). П’ятий стовпчик містить P-значення (P-value) для вказаних Т-статистик (зміст цього поняття роз’яснювався вище). Нагадаємо, що малість P-значення означає тут вказівку на те, що дані не підтверджують відповідну гіпотезу. По замовчуванню, саме поняття «малість P-значення» означає тут «менше 0,05».

1.2. Таблиця Analysis of Variance.

Розглядувана таблиця має вигляд:

Source	Sum of Squares	Df	Mean Squares	F-ratio	P-value
Model Residual
Total (Corr.)

Дана таблиця (у перекладі: таблиця дисперсійного аналізу) містить результати наступних обчислень.

У другому стовпчику, що має назву «суми квадратів» (Sum of Squares) наводяться три суми квадратів, що відповідають назвам з першого стовпчика Source – джерело: обумовлена регресією – Model, остаточна – Residual і загальна (скоректована) – Total (Corr.). Перша сума квадратів дорівнює 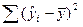, друга дорівнює S( y_i – ŷ_i)², і, нарешті, третя дорівнює 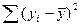. Згідно з рівністю (3.3) Model + Residual = Total (Corr.).

Третій стовпчик Df містить «ступені волі», що відповідають вищезазначеним сумам: 1, n – 2 і n – 1 відповідно — див. зауваження 4.3.6, 4.3.8 та вправу 4.3.7.

У четвертому стовпчику Mean Squares даються середні суми квадратів, що відповідають першим двом сумам: Model / 1 і Residual / (n – 2).

П’ятий стовпчик (F-ratio) містить відношення (F-відношення) щойно вказаних середніх сум квадратів.

Шостий стовпчик (P-value) містить P-значення для F-відношення, що наводиться у зв’язку з перевіркою гіпотези про незначущість регресії (див. зауваження 4.3.8).

1.3. Перелік обчислених характеристик моделі

У списку, що подано після таблиці Analysis of Variance, містяться значення характеристик якості одержаної моделі. Прокоментуємо деякі з них.

Correlation Coefficient — дається значення оцінки коефіцієнту кореляції 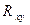між незалежною та залежною змінними 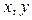- рівність (3.11).

R - Squared — дається (в процентах) значення коефіцієнту детермінації R², що визначений рівністю (3.5). Зауважимо, що ця величина (у символічному запису) дорівнює

(Model / Total (Corr.)) × 100 % .

Standard Error of Est. — дається числове значення оцінки середньоквадратичного відхилення моделі. При цьому в якості оцінки береться корінь з величини S², визначеної рівністю (4.15). Зокрема, виконується співвідношення

Standard Error of Est. = (Residual Mean Square)^{1 / 2}.

1.4. Durbin – Watson statistic — дається значення так званої статистики Дарбіна – Уотсона і P-значення для неї. За допомогою цієї статистики перевіряється гіпотеза про відсутність кореляції між компонентами вектора помилок моделі. Гіпотеза відхиляється (тобто дані свідчать про наявність кореляції) при достатньо малому P-значенні.

1.5. Lag 1 residual autocorrelation — наводиться значення оцінки коефіцієнта кореляції між суміжними компонентами вектора помилок.

2. Зміст таблиць, значень параметрів і коментарів у інших роздруківках пакету програм STATGRAPHICS, які треба одержати для виконання запланованих лабораторних робіт з регресійного аналізу, в основному, мало відрізняється від розглянутих вище.