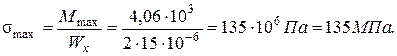Методические указания к решению задачи № 1

ЗАДАЧА № 1

Для двух стальных балок и чугунной балки (рис. 4.75)

требуется:

1) построить эпюры поперечных сил и изгибающих моментов;

2) подобрать поперечные сечения балок:

а) для стальной балки (рис. 4.75, а) - двутавровое; прямоугольное высотой h и основанием b при соотношении сторон h/b = 2; круглое - диаметром d;

б) для чугунной балки (рис. 4.75,б) определить размеры сечения из условия проч­ности по допускаемым напряжениям; форму сечения выбрать по рис.4.80;

в) для стальной балки (рис. 4.75,в) - сечение, состоящее из двух швел­леров.

Расчетные схемы балок и поперечных сечений выбираются по рис. 4.75 и 4.76, числовые данные берутся из табл. 4.1.

Числовые данные к задаче № 1

Таблица 4.1

Номер строки	Номер схемы	Сила P, кН	Момент М, кНм	Интенсивность распределенной нагрузки q, кН/м	Длина участка l, м	Допускаемые напряжения, МПа
Сталь	Чугун

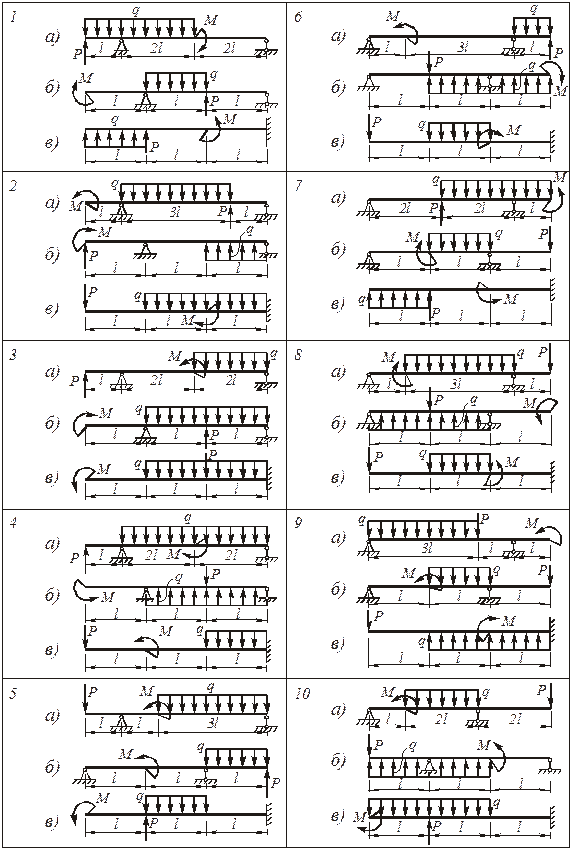
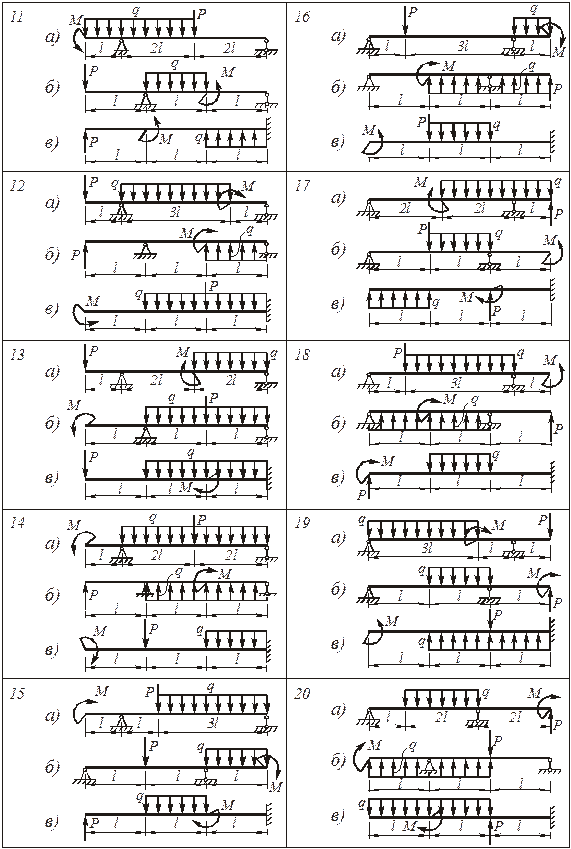
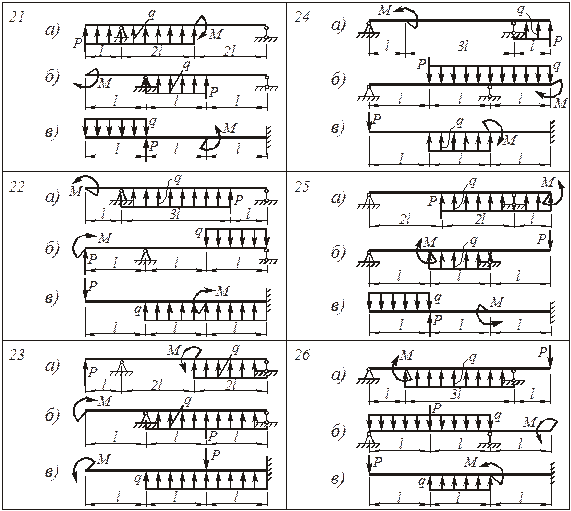
Рис. 4.75. Схемы балок к задаче № 1

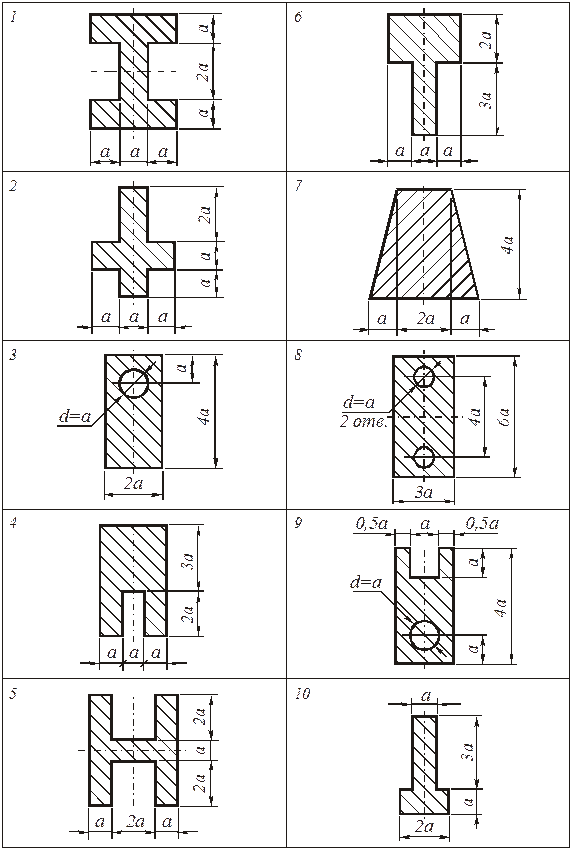
Рис. 4.76. Схемы поперечных сечений балок

Методические указания к решению задачи № 1

На рис.4.80 представлены схемы балок, для которых требуется построить эпюры поперечных сил Q, изгибающих моментов M и подобрать поперечные сечения из условия прочности балок при изгибе.

При решении подобных задач рекомендуется придерживаться следующего порядка расчета:

1. выписать из табл.4.1 исходные данные и вычертить схемы балок, показав на схеме их размеры и действующие нагрузки, включая опорные реакции. Истинное направление опорных реакций заранее указать затруднительно, поэтому в шарнирных опорах вертикальные реакции, как правило, направляют вверх. Горизонтальная составляющая реакции шарнирно неподвижной опоры равна нулю, так как при изгибе все внешние силы перпендикулярны оси балки;

2.составить уравнения статики, из которых определяются опорные реакции. Для балок, опирающихся на шарнирные опоры, составляют два уравнения равновесия: сумма моментов всех нагрузок, приложенных к балке, включая опорные реакции, относительно каждой из опор равна нулю

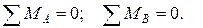
Примечания:

- построение эпюр Q и М для балки с защемлением при соблюдении некоторых ограничений не требует обязательного определения опорных реакций;

- если в результате расчета величина опорной реакции оказалась отрицательной, следует изменить ее первоначальное направление на противоположное;

3. проверить правильность определения опорных реакций. С этой целью составляется еще одно уравнение равновесия балки. Для балок, опирающихся на шарнирные опоры, приравнивается нулю сумма проекций всех сил, приложенных к балке, включая опорные реакции, на нормаль к ее оси. Если опора балки представляет собой защемление (заделку), составляется сумма моментов сил, приложенных к балке (включая уже вычисленные реакции в заделке), относительно ее любого сечения и приравнивается нулю. При отсутствии ошибки в расчете это уравнение статики удовлетворяется. Если же уравнения статики не удовлетворяются, проверяется правильность записи уравнений равновесия и их решение;

4. по правилам, изложенным выше в разделе «Основные теоретические сведения и расчетные формулы», строятся эпюры поперечных сил и изгибающих моментов.

Примечания: в решении задачи 1в для построения эпюр Q и M применяетсяаналитический способ - с записью уравнений 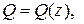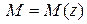. Умение правильно записывать формулы для вычисления поперечной силы и изгибающего момента в произвольно выбранном сечении необходимо при решении ряда задач курса «Сопротивление материалов»;

5. из условия прочности балки по нормальным напряжениям подбирается ее поперечное сечение.

Примечания:

- условие прочности по нормальным напряжениям для балок, материал которых имеет одинаковые прочностные характеристики при растяжении и сжатии, имеет вид

,

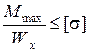где 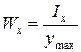- осевой момент сопротивления поперечного сечения, 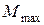- максимальный по абсолютной величине изгибающий момент в поперечном сечении балки, 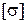- допускаемое нормальное напряжение материала балки;

- величина требуемого осевого момента сопротивленияпри подборе сечения балки из условия ее прочности определяется формулой

.

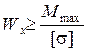По найденному значению 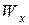подбираются размеры поперечного сечения заданной формы, либо по таблицам сортамента - соответствующий прокатный профиль;

- если материал балки имеет различные прочностные характеристики при растяжении и сжатии (хрупкие и хрупко – пластические материалы), рекомендуется выбирать ее поперечное сечение, несимметричным относительно нейтральной оси. Располагать его следует таким образом, чтобы в опасном сечении балки, в сжатой зоне, находились бы волокна, наиболее удаленные от нейтральной оси. Опасным сечением при эпюре одного знака (в каждом сечении балки изгибающий момент либо положительный, либо отрицательный) будет то, в котором возникает максимальный по абсолютной величине изгибающий момент (расчетный момент). Если эпюра изгибающих моментов имеет участки, на которых 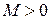, и участки, где 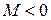, производится дополнительная проверка прочности балки по растягивающим напряжениям в поперечном сечении, имеющем наибольший изгибающий момент, знак которого противоположен расчетному моменту.

ПРИМЕР РЕШЕНИЯ ЗАДАЧИ №1

Задача 1, а

Для стальной балки (рис.4.77) требуется:

1. построить эпюры поперечных сил и изгибающих моментов;

2. подобрать три типа поперечных сечений балки: двутавровое; прямоугольное высотой h и основанием b (при соотношении сторон h/b = 2); круглое - диаметром d.

Исходные числовые данные: P = 2 кН, М = 8 кНм, q = 4 кН /м, l = 1м, допускаемое напряжение 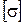= 160 МПа.

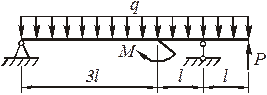
Рис.4.77. Заданная схема балки

Решение.

1. Построение эпюры поперечных сил и изгибающих
моментов

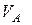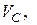1.1. Выписываем из табл.4.1 исходные данные. Вычерчиваем расчетную схему балки (рис. 4.78), показав на схеме ее размеры и действующие нагрузки, включая опорные реакции и направляя их вверх.

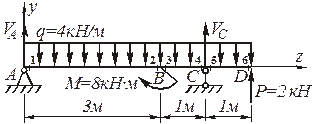
Рис. 4.78. Расчетная схема балки

1.2. Определение опорных реакций из условий равновесия балки:

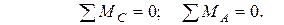
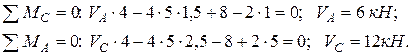
1.3. Проверка правильность вычисления опорных реакций:

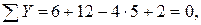
Поскольку уравнение равновесия балки удовлетворяется, реакции определены правильно.

1.4. Построение эпюр поперечных сил и изгибающих моментов на основе дифференциальных зависимостей Д.И. Журавского с вычислением поперечных сил и изгибающих моментов в характерных сечениях.

1.4.1.Для построения эпюр поперечных сил и изгибающих моментов балка разбивается на три участка - AB, BC, CD, начало координат - в крайнем левом сечении балки (рис. 4.78).

1.4.2. Вычисления значений Q и M на границах участков (слева и справа от граничных сечений) и построение эпюр поперечных сил и изгибающих моментов.

Участок AB.

сечение 1 (начало первого участка):

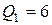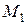кН, = 0;

сечение 2 (конец первого участка):

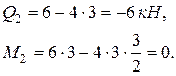
Участок BC

сечение 3 (начало второго участка):

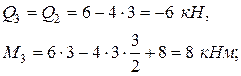
сечение 4 (конец второго участка):

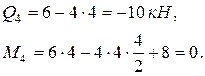
Участок CD

сечение 5 (начало третьего участка):

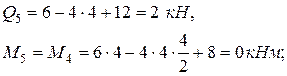
сечение 6 (конец третьего участка):

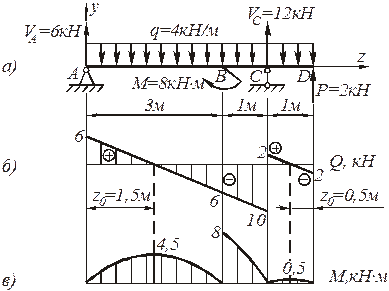
Рис.4.79. Расчетная схема балки, эпюры поперечных сил и изгибающих моментов: а) расчетная схема балки; б) эпюра поперечных сил; в) эпюра изгибающих моментов

В выбранном масштабе от оси эпюры вверх отложены вычисленные положительные значения поперечных сил, вниз – отрицательные (рис.4.79,б).

Поскольку эпюра Q дважды пересекает свою ось, изменяя знак с плюса на минус, в сечениях F и G изгибающие моменты экстремальны ( 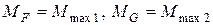). Из рис. 4.84,б следует, что сечения F и G расположены посередине участков AB и CD.

Вычисление экстремальных моментов :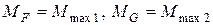

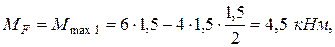
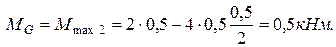
Эпюра изгибающих моментов, построенная на сжатом волокне (положительные значения изгибающих моментов отложены вверх, отрицательные – вниз) показана на рис. 4.79,в.

Примечание: студенты строительных специальностей откладывают положительные значения изгибающих моментов вниз от оси эпюры, и выпуклость параболы направлена по направлению вектора силы равномерно распределенной нагрузки.

5. Подбор поперечного сечения балки из условия ее прочности по нормальным напряжениям

5.1. Подбор двутаврового сечения

Требуемый из условия прочности осевой момент сопротивления поперечного сечения

.

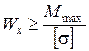Учитывая, что по условию задачи 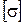= 160 МПа и наибольший по абсолютной величине изгибающий момент 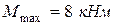(рис.4.79,в), требуемый осевой момент сопротивления

.

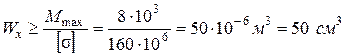Номер двутаврового сечения, имеющего осевой момент сопротивления, близкий к требуемому, подбираем по таблице сортамента (ГОСТ 8239-72). Принимаем двутавр № 12, для которого .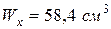

Максимальное нормальное напряжение, действующее в балке, поперечное сечение которой двутавр № 12

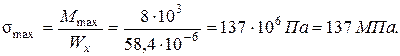
5.2. Подбор прямоугольного сечения

Осевой момент сопротивления прямоугольного сечения 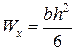, при заданном соотношении :

.

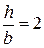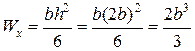Тогда

, , .

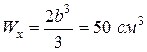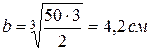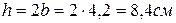5.3. Подбор круглого сечения.

Осевой момент сопротивления круглого сечения 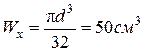и искомая величина диаметра поперечного сечения балки

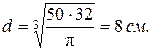
Задача 1,б

Для чугунной балки (рис. 4.80) требуется:

1.построить эпюры поперечных сил и изгибающих моментов;

2.определить размеры поперечного сечения из условия проч­ности балки по допускаемым напряжениям.

Форма сечения изображена на рис. 4.81.

Исходные числовые данные: Р₁=4кН, Р₂=3Р₁=12кН М=6 кНм,
q=8 кН/м, l = 1м, допускаемое напряжение чугуна на растяжение 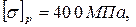допускаемое напряжение на сжатие - .

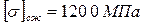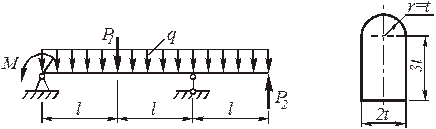
Рис. 4.80. Заданная схема балки Рис. 4.81.Схема поперечного сече ния балки

Решение.

1. Построение эпюры поперечных сил и изгибающих
моментов

1.1. Вычерчиваем расчетную схему балки, показав на схеме ее размеры и действующие нагрузки, включая опорные реакци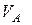и и 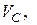направляя их вверх (рис.4.82).

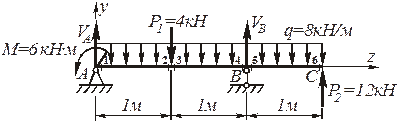
Рис. 4.82. Расчетная схема заданной балки

1.2. Определение опорных реакций из условий равновесия балки:

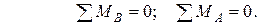
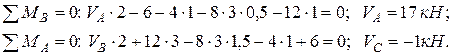
1.3. Проверка правильность вычисления опорных реакций:

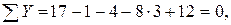
Поскольку уравнение равновесия балки удовлетворяется, реакции определены правильно.

1.4. Построение эпюр поперечных сил и изгибающих моментов на основе дифференциальных зависимостей Д.И. Журавского с вычислением поперечных сил и изгибающих моментов в характерных сечениях.

1.4.1. Для построения эпюр поперечных сил и изгибающих моментов балка разбивается на три участка - AD, DB, BC, начало координат - в крайнем левом сечении балки (рис. 4.87,а).

1.4.2. Вычисления значений Q и M на границах участков (рис. 4.82), слева и справа от граничных сечений. Построение эпюр поперечных сил и изгибающих моментов.

Участок AD.

сечение 1 (начало первого участка):

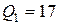кН, 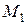= -6 кНм;

сечение 2 (конец первого участка):

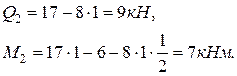
Участок DB

сечение 3 (начало второго участка):

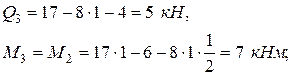
сечение 4 (конец второго участка):

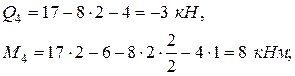
Участок DC

сечение 5 (начало третьего участка):

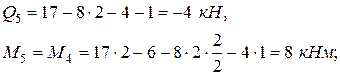
сечение 6 (конец третьего участка):

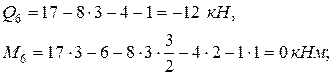
Поскольку эпюра Q в пределах участка CB пересекает свою ось, изменяя знак с плюса на минус, в некотором сечении этого участка балки изгибающий моменты экстремален 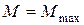. Обозначив расстояние этого сечения от начала участка CB через 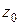и приравнивая поперечную силу, действующую в этом сечении нулю, определяем численное значение величины :

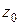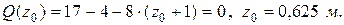
Экстремальный момент

:

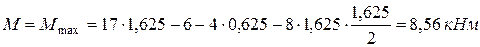Эпюры поперечных сил и изгибающих моментов представлены на

рис. 4.83.

Рис. 4.83. Расчетная схема балки. Эпюры поперечных сил и изгибающих моментов: а - расчетная схема балки; б - эпюра поперечных сил;

в - эпюра изгибающих моментов.

2.Определение размеров поперечного сечения из условия проч­ности балки по допускаемым напряжениям.

2.1.Вычисление геометрических характеристик заданного сечения.

2.1.1. Определение положения центра тяжести сечения балки.

Для определения размеров поперечного сечения все геометрические характеристики выражаются через параметр t и заданное сечение вычерчивается в масштабе (рис.4.84).

Сечение рассматривается в исходной (начальной) системе координат. Ось ординат y_с, совмещается с осью симметрии фигуры, ось абсцисс x – с ее основанием.

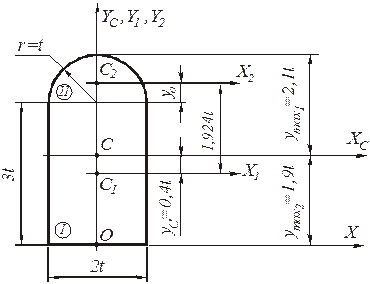
Рис. 4.84. Схема к вычислению геометрических

характеристик поперечного сечения

Заданное составное сечение разбивается на элементы, представляющие собой две простые геометрические фигуры: I - прямоугольник, II – полукруг.

Центры тяжести составляющих фигур и всей заданной фигуры (сечения) лежат на оси симметрии y_с , которая является их главной центральной осью.

В исходной системе координат x, y_с центры тяжести составляющих фигур (С₁, С₂) определяются по рис. 4.84. Ордината точки С₁ 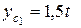и учитывая, что

,

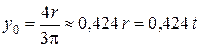вычисляем ординату точки С₂:

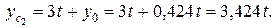
Заданная фигура имеет ось симметрии (ось Y_с,), центр тяжести лежит на этой оси, поэтому достаточно вычислить одну из его координат - ординату y_c:

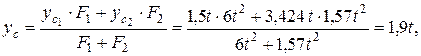
где 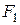- площадь прямоугольника, 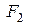- площадь полукруга.

Отложив на оси Y_с, отрезок ОС = y_c= 1,9 a, строим точку С - центр тя­жес­ти составного сечения (рис. 4.84) и проводим параллельно начальной оси X главную центральную ось X_С составной фигуры и главные центральные оси составляющих фигур I, II, параллельные исходным осям x, y_с, соответственно обозначенные x₁, y₁ и x₂, y₂.

2.1.2. Вычисление площадей и главных моментов инерции составляющих фигур относительно собственных центральных осей.

Для каждой из составляющих простых геометрических фигур вычисляются площадь и осевой момент инерции относительно собственной главной центральной оси, параллельной исходной:

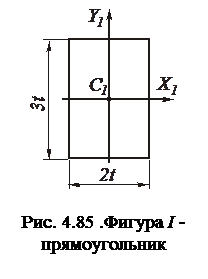
прямоугольник (рис. 4.85)

,

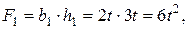
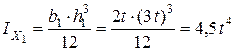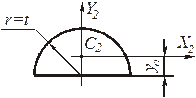
Рис. 4.86. Фигура II полукруг

,

.

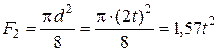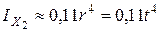2.1.3. Вычисление моментов инерции составляющих фигур относительно главной центральной оси X_C.

Вычисление моментов инерции составляющих фигур относительно главной центральной оси X_C производится по формулам

, .

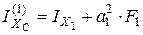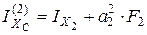Считая главные центральные оси x₁, X₂ каждойиз составляющих фигур исходными, (расстояния между осями 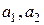определяется по рис.4.89), получим:

- для прямоугольника

,

;

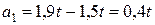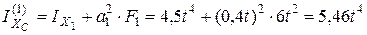- для полукруга

,

.

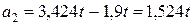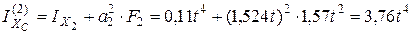2.1.3. Вычисление главного центрального момента инерции сечения балки относительно главной центральной оси X_C.

Главный центральный мо­мент инерции составной фигуры относительно оси X_C представляет собой сумму осевых моментов инерции составляющих фигур относительно этой же оси

.

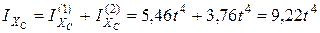2.2.Определение размеров поперечного сечения из условия проч­ности балки.

2.2.1. Определение осевого момента сопротивления при изгибе

Для балки, изготовленной из хрупкого материала, вычисляем два момента сопротивления относительно оси X_C:

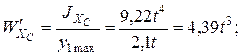
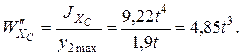
2.2.2. Определение размеров сечения из условия прочности балки.

В сечении, где изгибающий момент 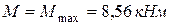(рис. 4.88,в), нижние волокна балки растянуты, верхние волокна сжаты. Условие прочности для опасной, наиболее удаленной от нейтральной оси точки в растянутой зоне сечения имеет вид

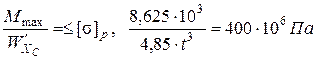
Из последнего выражения определяем искомый параметр t

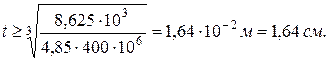
Наибольшие сжимающие напряжения в рассматриваемом сечении

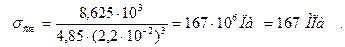
Условие прочности по сжимающим напряжениям 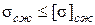, 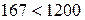удовлетворяется.

Так как условия прочности по растягивающим и сжимающим напряжениям удовлетворяются, величина параметра принимается t = 1,64 см.

Задача 1,в

Для стальной балки (рис.4.87), состоящей из двух швеллеров [], требуется:

1. построить эпюры поперечных сил и изгибающих моментов;

2. подобрать поперечное сечение балки из условия проч­ности балки по допускаемым напряжениям.

Исходные числовые данные: P=3кН, М=4кНм,
q₁ =4 кН/м, q₂=2q₁ = 8 кН/м, l = 1м, допускаемое напряжение 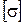= 160 МПа.

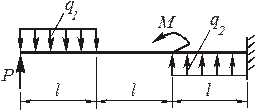
Рис.4.87. Заданная схема балки

1. Построение эпюр поперечных сил и изгибающих

моментов

1.1. В соответствии с исходными данными вычерчиваем расчетную схему балки, на которой показываем опорные реакци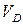и и 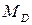. Реакцию 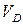направляем вверх, опорный момент 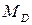- по часовой стрелке (рис.4.88).

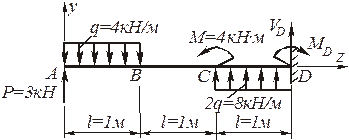
Рис.4.88. Расчетная схема заданной балки

1.2. Определение опорных реакций из условий равновесия балки:

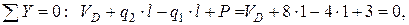
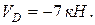
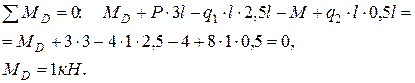
Так как одна из реакций опор отрицательна (реакция 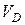), ее направление изменяется на противоположное, а направление опорного момента остается без изменений.

1.3. Проверка правильность вычисления опорных реакций:

Для проверки вычислений составляется уравнение равновесия балки, в которое входили бы обе опорные реакции:

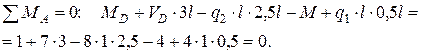
Уравнение равновесия при найденных величинах реакций удовлетворяется.

1.4. Построение эпюр поперечных сил и изгибающих моментов аналитический способом.

1.4.1. Разбиение балки на участки. Составление уравнений для вычисления 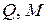и их определение в граничных сечениях.

Для записи уравнений 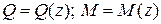разбиваем балку на три участка - AB, BC, CD, в пределах которых эти уравнения справедливы. Начало координат - в крайнем левом сечении балки (рис. 4.89).

В пределах каждого участка выбираем произвольное сечение на расстоянии z от начала координат и составляем выражения для вычисления Q и M: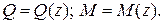

Участок AB (0<z<1).

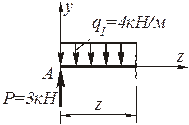
Рис. 4.89. К определению поперечной силы Q и изгибающего

момента М в произвольном сечении z участка АВ

Поперечная сила, действующая в рассматриваемом сечении, определяется из выражения

.

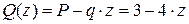Она линейно зависит от переменной z, следовательно, эпюра Q ограничена наклонной прямой.

Изгибающий момент

.

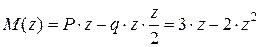Эпюра изгибающего момента в пределах участка AB ограничена квадратной параболой выпуклой вверх.

Примечание: при записи уравнения 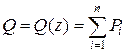и 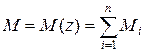знаки поперечной силы Q и изгибающего момента M определяются с помощью рис. 4.16 и рис. 4.17.

Поперечная сила в начале и конце участка AB:

начало участка, сечение А, z =0,

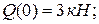
конец участка, сечение В, z = 1м,

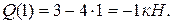
Поскольку поперечная сила на участке AB изменила знак с плюса на минус, проходя при этом через ноль, в сечении с абсциссой z₀, изгибающий момент имеет мак­си­мум.

Расстояние z₀ найдем из выраже­ния:

Q (z₀ ) = P - q· z₀ = 3 - 4· z₀ = 0 .

Очевидно, что

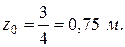
Изгибающий момент в начале и конце участка AB:

начало участка, сечение А, z =0,

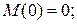
конец участка, сечение В, z =1м,

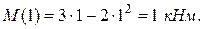
Эпюра изгибающего момента в пределах участка AB ограничена квадратной параболой выпуклой вверх и имеющей максимум.

Максимальный изгибающий момент в сечении с абсциссой z₀

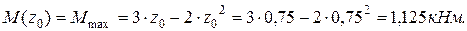
Участок BС (1<z<2).

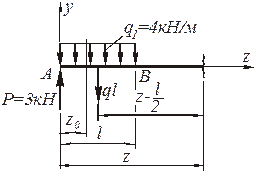
Рис. 4.90. К определение поперечной силы Q и изгибающего

момента М в произвольном сечении z участка ВС

Поперечная сила, действующая в рассматриваемом сечении (рис.4.90)

,

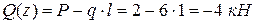Поперечная сила не зависит от переменной z на протяжении всего участка, и эпюра Q ограничена прямой, параллельной ее оси.

Изгибающий момент

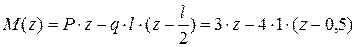
Поскольку изгибающий момент линейно зависит от переменной z, эпюра М ограничена наклонной прямой.

Изгибающий момент в начале и конце участка BС:

начало участка, сечение В, z = 1м,

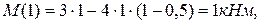
конец участка, сечение C, z =2м,

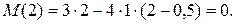
Участок СD (2<z<3).

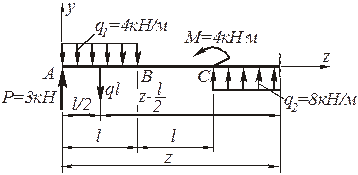
Рис. 4.91. К определению поперечной силы Q и изгибающего

момента М в рассматриваемом сечении z участка СD

Поперечная сила в рассматриваемом сечении с абсциссой z (рис. 4.91):

.

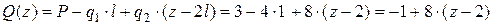Поперечная сила линейно зависит от переменной z, эпюра Q ограничена наклонной прямой.

Изгибающий момент в рассматриваемом сечении с абсциссой z

.

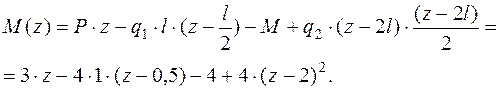Эпюра изгибающего момента в пределах участка СD ограничена квадратной параболой выпуклой вниз.

В сечении С приложена пара сил, что на эпюре изгибающих моментов вызывает скачок, величина которого равна величине приложенной пары.

Поперечная сила в начале и конце участка СD:

начало участка, сечение C, z =2 м

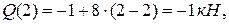
конец участка, сечение D, z = 3м,

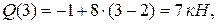
Поскольку поперечная сила на участке СD изменила знак с минуса на плюс, проходя при этом через ноль, в сечении с абсциссой z₀₁, изгибающий момент имеет мини­мум. Расстояние z₀₁ найдем из выраже­ния:

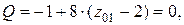
очевидно, что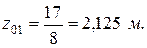

Изгибающий момент в начале и конце участка СD:

начало участка, сечение C, z = 2м,

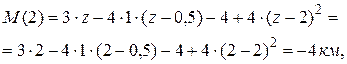
конец участка, сечение D, z = 3м,

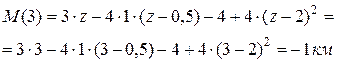
Эпюра изгибающего момента в пределах участка СD ограничена квадратной параболой выпуклой вниз и имеющей минимум.

Минимальный изгибающий момент в сечении с абсциссой z₀₁ = 2,125м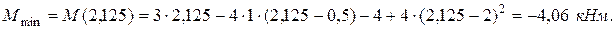

Построение эпюр поперечных сил Q и изгибающих моментов М.

Эпюрыперечных сил Q и изгибающих моментов М строятся в выбранном масштабе по их значениям на границах участков. Положительные величины откладываются вверх от оси эпюры (эпюра строится на сжатом волокне), отрицательные – вниз. Эпюрыпоперечных сил Q и изгибающих моментов М показаны на рис. 4.92,б,в.

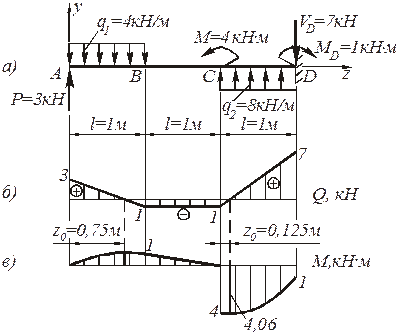
Рис. 4.92. Расчетная схема балки. Эпюры поперечных сил и изгибающих

моментов: а - расчетная схема балки; б - эпюра поперечных сил; в - эпюра

изгибающих моментов

2. Подбор поперечного сечения

2.1.Определение требуемого осевого момента сопротивления поперечного сечения.

Из условия прочности при изгибе требуемый осевой момент сопротивления

.

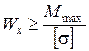Учитывая, что по условию задачи 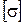= 160 МПа и максимальное по абсолютной величине значение изгибающего момента 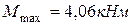, определяем значение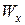

.

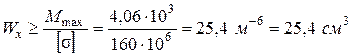Заданное сечение является составным, включающим два одинаковых швеллера.

Осевой момент сопротивления подобного сечения определяется по формуле

.

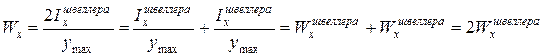Таким образом, требуемый по условию прочности осевой момент сопротивления швеллера

.

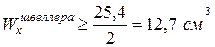Номер швеллера, имеющего осевой момент сопротивления, близкий к требуемому, определяем по таблице сортамента (ГОСТ 8240-72). Принимаем швеллер № 6,5, для которого .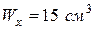

Максимальное нормальное напряжение, действующее в балке, поперечное сечение которой состоит из двух швеллеров № 6,5