Описание опытной установки. Опытная установка (рис. 1) состоит из напорного бака 1 с водой, трубопровода 2, на котором установлены:

Опытная установка (рис. 1) состоит из напорного бака 1 с водой, трубопровода 2, на котором установлены:

- шаровый кран 3 и 4;

- вентили 5, 6 и 7;

- пьезометры №9÷№14.

Мерный бак 8 служит для определения объемным методом расхода воды протекающего по трубопроводу 2. После от­крытия крана 3 вода из бака поступает в трубопровод 2. С помощью крана 4 устанавливается расход воды в трубопроводе 2.

Порядок проведения лабораторной работы

1. Открыть кран 3, с помощью крана 4 установить расход Q воды в трубе 2.

2. С помощью секундомера определить время t наполнения слоя воды с в мерном баке 8.

3. Замерить разность уровней жидкости в пьезометрах: h_9-10, h_11-12, h_12-14, h_11-14.

4. Закончив измерения, закрыть кран 4.

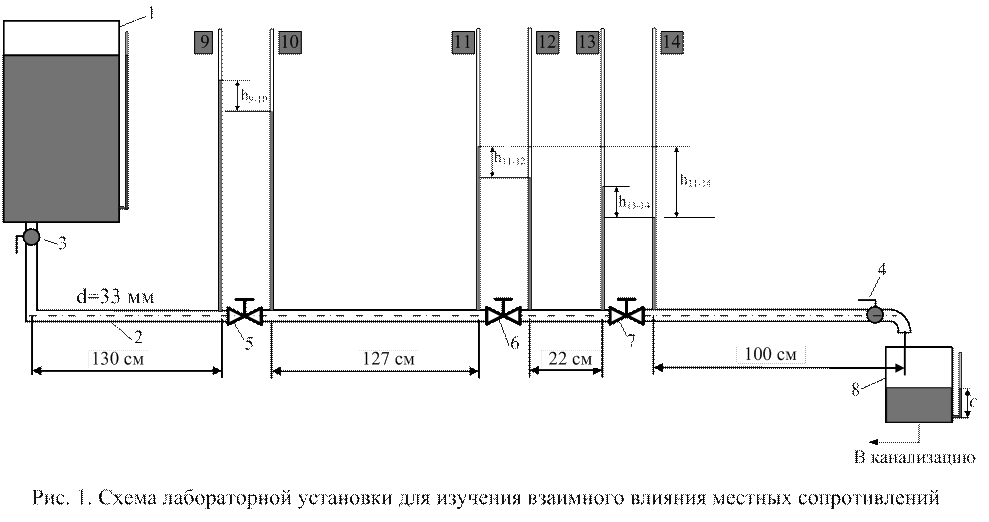
Таблица 1

Экспериментальные данные и обработка результатов

Величины

Ед. изм.

Номера опытов

I

II

III

Потери напора

h9-10

h11-12

h12-14

h11-14

h9-10

h11-12

h12-14

h11-14

h9-10

h11-12

h12-14

h11-14

см

Высота слоя воды в мерном баке, с

см

Время наполнения, t

с

Объем воды, V

см3

Расход, Q = V / t

см/с

Диаметр, d

см

3,3

Площадь,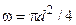

см2

Скорость,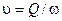

см/с

Коэффициент местного сопротивления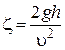

б. р.

Число Рейнольдса,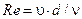

б. р.

Обработка опытных данных

1. Определить объем воды V, см³, заполнения мерного бака. Размеры мерного бака: а=19 см, b=44 см.

.

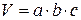2. Определить расход Q,зная время t, с, заполнения объема воды V в мерном баке по формуле:

.

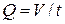3. Определить скорости движения воды в трубе 2 зная, что:

,

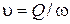где 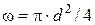– площадь поперечного сечения трубы.

4. Определить значение числа Рейнольдса

,

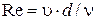где ν – кинематический коэффициент вязкости воды, .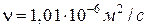

5. Для каждого замера подсчитать значение коэффициента местного сопротивления по формуле

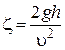
6. Сравнить значение ζ для вентиля 5 со значениями ζ для вентилей 6 и 7. Сделать вывод о результатах сравнения.

7. Данные занести в табл. 1.

8. Привести пример расчета.

ЛАБОРАТОРНАЯ РАБОТА № 8

«ИССЛЕДОВАНИЕ ИСТЕЧЕНИЯ ЖИДКОСТИ ЧЕРЕЗ МАЛЫЕ ОТВЕРСТИЯ В ТОНКОЙ СТЕНКЕ И НАСАДКИ»

Цель работы

1. Экспериментальное определение коэффициентов расхода, скорости, сжатия и сопротивления при истечении жидкости из малого круглого отверстия в тонкой стенке и насадки при постоянном напоре и сравнение полученных значений со справочными.

2. Наблюдение инверсии струи, вытекающей из отверстий различного очертания.

3. Измерение вакуума в насадке Вентури.

Общие сведения

Истечение из отверстия. Рассмотрим истечение жидкости плотностью из резервуара через малое незатопленное отверстие (рис. 1, а). Глубина погружения центра тяжести отверстия под свободной поверхностью равна H (напор).

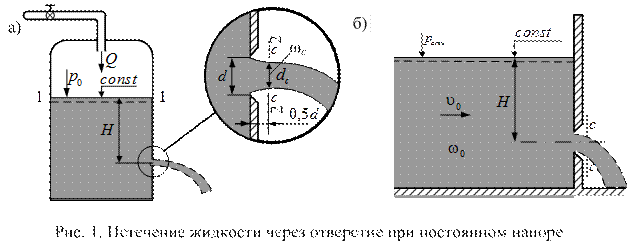
Истечение происходит при постоянном напоре, то есть уровень жидкости в резервуаре является неизменным. Это возможно, если свободная поверхность жидкости занимает большую площадь (рис. 1, б) или если в резервуар подается такой же расход, что и вытекает через отверстие (рис. 1, а).

При постоянном напоре скорости истечения будут неизменными во времени, то есть движение будет установившимся. При этом линии тока и траектории движения частиц жидкости совпадают.

Малым отверстием называется такое, у которого наибольший вертикальный размер d не превышает 0,1H. При выполнении этого условия скорости на верхней и нижней границах вытекающей из отверстия струи можно считать одинаковыми.

Траектории частиц при приближении к отверстию искривляются. Действующая центробежная сила направлена внутрь формирующейся струи. Сечения струи постепенно уменьшаются. Поэтому площадь сечения струи ω_c меньше отверстия ω₀. Отношение 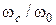называется коэффициентом сжатия ε для малых отверстий.

Сжатие продолжается и на некотором расстоянии от плоской стенки после выхода струи из резервуара. Движение жидкости на этом участке вблизи стенки неравномерное. Живые сечения потока на этом участке криволинейные, постепенно уменьшающиеся. По мере удаления от отверстия кривизна линий тока уменьшается, и на некотором расстоянии от стенки движение приближается к плавно изменяющемуся.

При истечении реальной жидкости из резервуара через малое отверстие при условии, что уровень жидкости в резервуаре остается постоянным, уравнение Бернулли, записанное для сечений I и II относительно некоторой плоскости сравнения 0-0, примет вид:

.

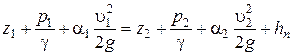Сумма левой и правой части уравнения и первые три слагаемые в правой представляют удельные энергии жидкости, отнесенные к единице ее веса (напоры) в рассматриваемых сечениях. Формула потерь напора при прохождении жидкости через отверстие имеет вид:

,

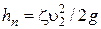где z – коэффициент местного сопротивления.

Считая 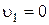получили, что средняя скорость вытекающей струи:

,

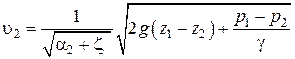где 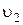– действительная скорость истечения реальной жидкости ( ).

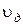Обозначив разность геометрических напоров z₁ – z₂ = h и считая α₁ = 1 получим:

,

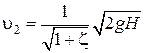где 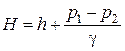– действительный напор. Чаще всего 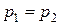, поэтому:

,

,

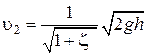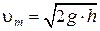где 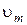– теоретическая скорость или скорость истечения идеальной жидкости ( ):

,

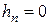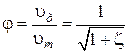где 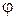– коэффициент скорости. Здесь .

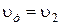Действительный расход через малое отверстие равен:

,

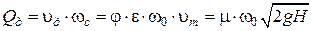так как ,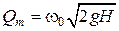

то 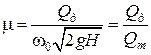или, ,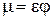
где µ – коэффициент расхода.

При Re < 10⁵ коэффициенты 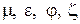являются функцией числа Re. При Re ˃ 10⁵ перечисленные коэффициенты имеют следующие численные значения: µ=0,62, φ=0,97, ε=064, ζ=0,06.

Коэффициент скорости φ может быть определен координатным способом. Дальность полета струи x вытекающей из отверстия находящегося на высоте y над горизонтальной плоскостью может быть выражена как:

, ,

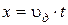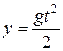где t – время полета струи до плоскости.

Из этих уравнений:

. .

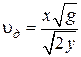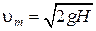Таким образом: .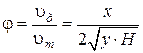

Коэффициент сопротивления определяется по формуле

.

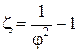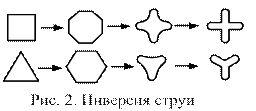
При истечении из отверстия происходит изменение сечения струи, называемое инверсией струи. Наиболее ярко это явление проявляется при истечении через отверстия полигональной формы. На рис. 2 показаны несколько примеров, характеризующих инверсию струи. При истечении через квадратное отверстие струя постепенно превращается в крест с тонкими прозрачными ребрами, ориентированными нормально к сторонам квадрата. Вытекающая через треугольное отверстие струя постепенно принимает форму звезды с ребрами, перпендикулярными сторонам тре­угольника. Объясняется это интересное и зрелищно красивое явление совместным действием поверхностного натяжения (благодаря которому углы сначала притупляются, а затем образуются «звезды») и инерции.

Истечение из насадков.Насадками называются короткие патрубки длиной 3 – 4 диаметра входного отверстия.

Различают цилиндрические, конические и коноидальные насадки, внутренняя поверхность которых выполнена в форме поверхности вытекающей струи.

Цилиндрические насадки делятся на внутренние (насадки Борда) и внешние (насадки Вентури, рис. 4), конические насадки могут быть сходящиеся и расходящиеся (рис. 3, а, в).

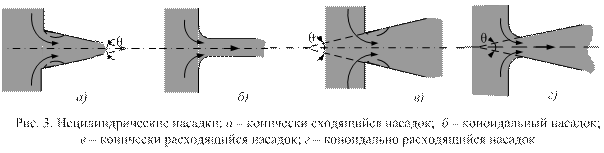
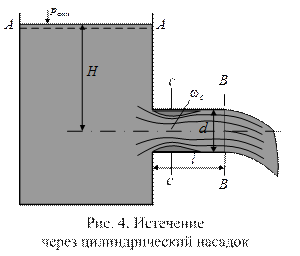Струя при входе в насадок, как и в отверстиях, претерпевает сжатие, далее расширяется и заполняет все сечение насадки. Над сжатым сечением образуется зона с пониженным (ниже атмосферного) давлением жидкости – область вакуумметрического давления. Сопротивление насадка обусловлено сжатием и последующим расширением струи. Коэффициент сопротивления z_н является суммой коэффициентов сопротивлений входа ζ_вх и расширения ζ_расш.

Струя жидкости на выходе из насадка заполняет его сечение полностью, то есть коэффициент сжатия насадки ε_н = 1 (рис. 4). Вакуум в сжатом сечении насадка увеличивает действующий напор. При турбулентном движении, когда потери напора по длине малы вследствие короткой длины насадка, а вакуум достигает примерно 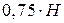, пропускная способность внешнего цилиндрического насадка существенно больше (до 33 %) при прочих равных условиях расхода через отверстие. При ламинарном истечении, потери по длине, соизмеримы с местными, вследствие малого сжатия величина вакуума не велика. Поэтому расход через насадок оказывается меньше расхода через отверстие. Записывая уравнение Бернулли для сечений А-А и В-В и считая, что u_А = 0, определим скорость истечения через насадок:

,

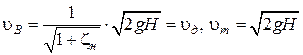где 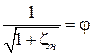– коэффициент скорости насадка;

u_д – действительная, а u_т – теоретическая скорость истечения.

Расход Q через насадок определяется как:

.

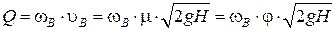Так как 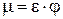, то при ε = 1, .

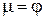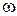– площадь сечения струи (или отверстия) на выходе из насадка.

Коэффициент скорости 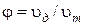может быть определен координатным методом по формуле:

,

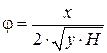где x = u_дt – дальность полета струи,

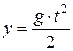– высота падения струи.

Тогда коэффициент сопротивления насадка 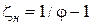. Следует заметить, что практически при одинаковых диаметрах входных отверстий z_вх насадков примерно равны.

Коэффициент z_н, в основном, зависит от z_расш = (ω₂ / ω₁ – 1)². Таким образом, с увеличением ω₂ при постоянном ω₁, (а ω₁, зависит только от Н) ζ_расш увеличивается. Соответственно растет ζ_н и уменьшается φ насадка. То есть у конически расходящихся насадков коэффициент φ и, соответственно, μ меньше, чем хотя бы у цилиндрических с тем же диаметром входного отверстия. Коэффициент расхода μ может быть определен как 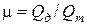путем замера действительного расхода Q_д и подсчета теоретического расхода 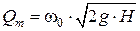, где ω₀ – площадь выходного отверстия.

Вакуум, образующийся над сжатым сечением струи в насадке оказывает всасывающее воздействие на струю, что ведет к увеличению скорости жидкости в сжатом сечении и к увеличению расхода через насадок в целом. Кроме того, с увеличением выходного отверстия, расход через насадок также увеличивается. Все это обусловливает повышенный расход через конически расходящийся насадок.

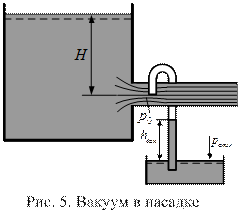При больших напорах Н струи истекающей жидкости (через конически расходящиеся и цилиндрические насадки) могут оторваться от стенок (явление срыва струи) за счет того, что давление в зоне сжатия струи (сечение С-С на рис. 3) станет меньше давления парообразования. В этом случае жидкость вскипает, и струя отрывается от стенки. Практически это наступает при значении вакуумметрического давления в зоне сжатия струи 6 ¸ 7 м вод. ст. Вакуумметрическое давление может быть измерено с помощью вакуумметра по схеме на рис. 5. Опыты показывают что h_вак = 0,75Н.

Расчетные зависимости при истечении жидкости через насадки те же, что и при истечении из отверстий, только в формулах ω – площадь насадка на выходе.

Для насадка Вентури в зоне квадратичного сопротивления определены численные значения коэффициентов: µ_н=φ_н= 0,82, ε_н=1, ζ_н=0,5.

При равенстве площадей 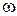и напоров Н расход зависит от 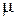, а кинетическая энергия – от 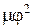, что и учитывают при сравнении отверстия и насадков. Осредненные данные этих параметров для больших чисел Re сведены в табл. 1.

Таблица 1

Осредненные данные φ, μ, z для отверстия и насадков

Отверстие и насадок	φ	μ	μφ2	z = 1/φ2 – 1
Отверстие в тонкой стенке	0,97	0,62	0,583	0,06
Внешний цилиндрический насадок	0,82	0,82	0,551	0,49
Конический сходящийся насадок (q = 13°)	0,97	0,95	0,894	0,06
Коноидальный насадок	0,97	0,97	0,913	0,06
Конический расходящийся насадок (данные отнесены к выходному сечению)	0,45	0,45	0,091	3,94

Проведем сравнение, как указывалось, при равенстве 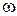и Н во всех случаях. Наибольшая скорость истечения, как видно из табл. 1, обеспечивается при истечении через отверстие в тонкой стенке, через сходящийся и коноидальный насадки. Максимальная пропускная способность наблюдается при истечении через расходящийся и коноидальный насадки.

Расход при истечении через внешний цилиндрический насадок больше, чем через отверстие в тонкой стенке, но вытекающая через отверстие струя обладает большей кинетической энергией, чем при истечении через внешний цилиндрический насадок.

Из всех сравниваемых устройств коноидальный насадок характеризуется максимальной кинетической энергией струи.

Расходящиеся насадки обеспечивают минимальные значения скорости и кинетической энергии струи. Наибольшее значение 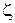у конически расходящегося насадка.