Некоторые выводы из закона всемирного тяготения

Ускорение у поверхности Земли. Сила тяжести.

Сила, с которой планета Земля притягивает тела, находящиеся у ее поверхности равна:

.

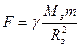И ускорение, с которым будут падать тела

,

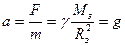не зависит от массы тела. Эта величина называется ускорением свободного падения и равна g=9,8 м/c². Являясь одинаковым для разных тел, ускорение свободного падения может отличаться в разных точках нашей планеты. Это является следствием того, что входящее в формулу

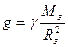
расстояние от центра масс Земного Шара до точки на поверхности Земли (R_з) может иметь различную величину в разных географических точках. Кроме того, влияние на величину g может оказать неоднородность по плотности земной коры.

Учитывая то, что ускорение свободного падения равно напряженности гравитационного поля у поверхности Земли, его используют для определения силы притяжения тел Земным Шаром (если эти тела находятся вблизи поверхности.). Эту силу называют силой тяжести:

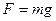
Потенциальная энергия вблизи поверхности Земли

Формула 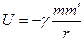предполагает, что 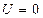на бесконечности. При учете потенциальной энергии объектов вблизи поверхности Земли удобнее задать нулевой уровень потенциальной энергии на поверхности Земли, то есть при r=R_з. Тогда потенциальная энергия тела, находящегося на высоте h (r=R_з +h)от поверхности будет равна:

.

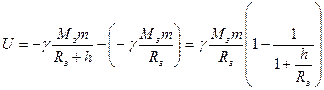Поскольку у поверхности Земли 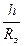<<1, можно считать, что

.

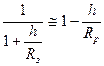Тогда, использовав, что 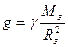, получим для потенциальной энергии вблизи поверхности Земли (в поле силы тяжести):

.

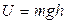Закон всемирного тяготения позволяет вычислить массу Земли и массу Солнца. Для определения массы Земли нужно знать радиус Земли. Он был определен по навигационным данным мореплавателей. (Rз=6400км). Гравитационная постоянная была измерена в лабораторных условиях. Тогда из

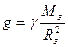следует .

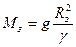Подставив числа, получим .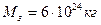

Для определения массы Солнца надо учесть, что благодаря притяжению Солнца Земля двигается по орбите с нормальным (центростремительным) ускорением равным 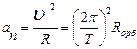, где R_орб – радиус орбиты Земли, а Т – период ее вращения вокруг Солнца (Т= 1год).

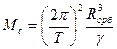
Первая и вторая космические скорости.

Первая космическая скорость не дает движущимуся телу упасть на Землю. Для того, чтобы спутник не упал на Землю сила притяжения Земли должна менять только направление скорости, то есть ускорение спутника должно равняться нормальному ускорению. Считая радиус орбиты приблизительно равным радиусу Земли, получаем

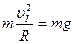
И .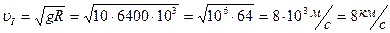

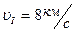- Первая космическая скорость

Вторая космическая скорость позволяет объекту освободиться от притяжения Земли, что произойдет, если этот объект улетит очень далеко от Земли (бесконечно далеко). На бесконечности потенциальная энергия равна нулю (если мы пользуемся формулой 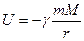). Кинетическую энергию на бесконечности тоже можем положить равной нулю, так как объект вышел из сферы притяжения Земли и нам неважно с какой скоростью он теперь двигается. По закону сохранения энергии при движении в потенциальном поле суммарная механическая энергия не изменяется, значит у поверхности Земли сумма потенциальной и кинетической энергии также равна нулю:

.

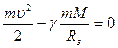Учитывая, что , получим

.

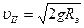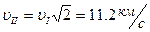- Вторая космическая скорость.