Зворотний хід
Із (Р3) 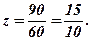
Із (Р2) 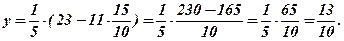
Із (Р1) 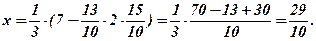
Перевірка. Підставимо 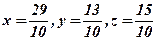 в СЛР(11), одержимо:
в СЛР(11), одержимо:
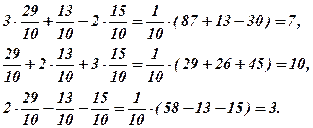
Відповідь. Система (11) має єдиний розв’язок: 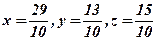 .
.
Приклад 2.Знайти розв’язок системи:
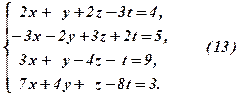
Складаємо обчислювальну таблицю.
Таблиця 3
| № п/п | Коефіцієнти при | Вільні члени | Суми | Контроль | |||
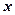 | 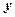 | 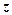 | 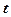 | ||||
  1 1 | |||||||
| -3 | |||||||
| -3 | -2 | ||||||
| -4 | -1 | ||||||
  4 4 | -8 | ||||||
| -1 | -5 | ||||||
| -1 | -14 | -2 | -2 | ||||
| -12 | -22 | -28 | -28 | ||||
  26 26 | -12 | ||||||
Таблиця 3 заповнюється за викладеною методикою. В 9-му рядку ми отримали нулі.
Тепер за даними таблиці 3 запишемо систему рівнянь, в які входять провідні елементи. Сюди включимо формально рівняння з елементами 9-го рядка, отримуємо:
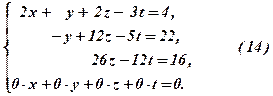
Останнє рівняння вигляду 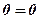 відкидаємо. Система (14) має трапецієподібну форму. Запишемо її в трикутній формі, для чого перенесемо в праві частини доданки з невідомим
відкидаємо. Система (14) має трапецієподібну форму. Запишемо її в трикутній формі, для чого перенесемо в праві частини доданки з невідомим 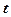 . Отже, маємо
. Отже, маємо
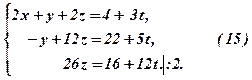
Далі зворотним ходом знаходимо:
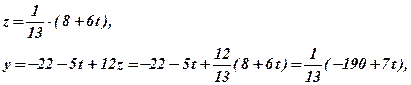
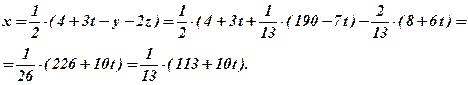
Остаточно:
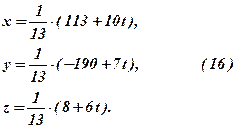
Рекомендується самостійно переконатись, що співвідношення (16) перетворюють СЛР(13) в тотожності, і отже, є розв’язком цієї системи при довільному значенні 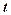 , яке називають вільнимневідомим, а
, яке називають вільнимневідомим, а 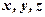 прийнято називати базисниминевідомими.
прийнято називати базисниминевідомими.
Так, наприклад, при 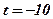 розв’язком буде:
розв’язком буде: 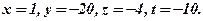
При
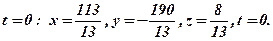
Прийнято називати розв’язок базисним, якщо при цьому вільні невідомі дорівнюють нулю.
Таким чином, система розв’язків (16) дає нескінченну множину розв’язків, якщо вільне невідоме 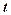 пробігає теж нескінченну множину значень.
пробігає теж нескінченну множину значень.
Приклад 3. Знайти розв’язок системи:
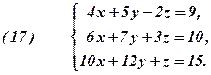
Розв’язання. Складаємо обчислювальну таблицю.
Таблиця 4
| № п/п | Коефіцієнти при | Вільні члени | Суми | Контроль | ||
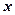 | 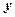 | 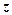 | ||||
  4 4 | -2 | |||||
  -2 -2 | -14 | |||||
| -2 |   24 24 | -30 | -8 | -8 | ||
За результатами таблиці 4 записуємо трикутну систему:
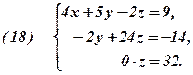
Останнє рівняння із системи (18), 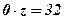 , розв’язку немає, отже і вся система (18), а, значить, і еквівалентна їй система (17) теж розв’язку немає, тобто несумісна.
, розв’язку немає, отже і вся система (18), а, значить, і еквівалентна їй система (17) теж розв’язку немає, тобто несумісна.
Зауваження 1. У викладеній схемі Гаусса ми зупинялись на випадках, коли елементи СЛР цілі числа. Якщо ж ці елементи виражаються десятковими дробами, то в основному поступають так:
1) вибирають серед всіх коефіцієнтів рівняння найбільший за абсолютною величиною (максимальний);
2) ставлять на першому місці в усіх рівняннях доданки з тим невідомим, де міститься цей коефіцієнт;
3)рівняння з максимальним коефіцієнтом переставляють на перше місце;
4)ділять перше рівняння почленно на максимальний коефіцієнт, в результаті провідний елемент стає рівним 1. Дальше застосовують правило прямокутника.
Зауваження 2. На практиці в схемі Гаусса користуються наближеними числами, внаслідок чого виникає похибка, тому ми отримуємо наближені розв’язки 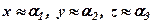 . Це, наприклад, для системи трьох рівнянь з трьома невідомими. Різниця між лівою частиною рівняння при
. Це, наприклад, для системи трьох рівнянь з трьома невідомими. Різниця між лівою частиною рівняння при 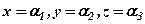 і правою частиною називається відхилом, позначається:
і правою частиною називається відхилом, позначається:
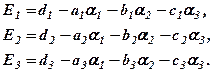
Відхили дають можливість оцінити точність отриманих розв’язків, крім того, можуть використовуватись для знаходження більш точних розв’язків.
