Деякі класичні приклади шифрів.

У Древній Греції (II в. до н.е.) був відомий шифр, називаний квадрат Полібія.

У квадрат розміром 5x5 кліток виписуються всі літери алфавіту, при цьому букви I,J не розрізняються (J ототожнюється з буквою I).

	A	B	C	D	E
A	A	B	C	D	E
B	F	G	H	I	K
C	L	M	N	O	P
D	Q	R	S	T	U
E	V	W	X	Y	Z

Буква, що зашифровувалася, замінялася на координати квадрата, у якому вона записана. Так, B замінялася на AB, F на BA, R на DB і т.д. При розшифруванні кожна така пара визначала відповідну букву повідомлення. Ключом такого шифра було розташування букв у таблиці 5x5.

Шифр Цезаря. Давньоримський імператор Юлій Цезар (100-44 р. до н.е.) застосовував шифр, при якому кожна літера тексту замінялася на літеру, розташовану в алфавіті на 9 позицій правіше від неї.

При виході за межі алфавіту, відповідний знак шифротексту вибирався з другого екземпляру алфавіту, що записувався слідом за першим. Це еквівалентно перетворенню латинського алфавіту за допомогою циклічного зсуву на 9 позицій вліво. Ключом є величина зсуву.

Пристрій шифрування скітала (V-IV вв. до н.е., Греція).

За описом Плутарха, пристрій складалося з двох ціпків однакової довжини і товщини. Ці ціпки називали скиталами. Скіталы зберігалися у кореспондентів. Для передачі повідомлення вирізували довгого і вузьку смугу папірусу, намотували неї на свою скіталу, не залишаючи на ній ніякого проміжку, так щоб смугою була охоплена уся поверхня ціпка.

Текст писали уздовж осі, знімали смугу і без ціпка відправляли адресатові. Тому що букви на ній розкидані довільно, то прочитати написане можна було тільки за допомогою скітали відповідного діаметру, намотавши на неї без пропусків смугу папірусу. Таким чином, діаметр скитали був секретним параметром.

Тема 2. Математичні основи криптографії

10. Алгебраїчні операції та алгебраїчні структури, які застосовуються в криптографії.

Множини з алгебраїчними операціями.

Нехай 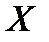- довільна множина. Бінарною (двомістною) алгебраїчною операцією (або законом композиції) на 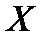називається відображення (правило) 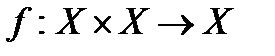, що будь-якій упорядкованій парі 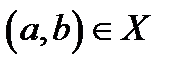ставить у відповідність визначений елемент 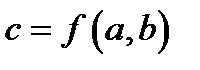множині 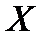. Замість 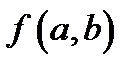пишуть 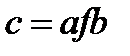. Часто бінарну операцію позначають спеціальним символом: *, °, ⋅ або +. На множині 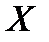може бути задано кілька різних операцій. 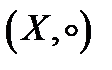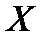Бажаючи виділити одну з них, скажемо, і говорять, що операція визначає на алгебраїчну структуру.

Напівгрупи і моноїды.

Бінарна операція на множині 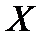називається асоціативною, якщо 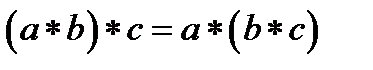для усіх 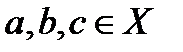. Вона також називається комутативною, якщо 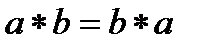.Ті ж самі назви використовуються для позначення відповідних властивостей алгебраїчної структури .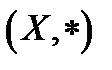