Озерский технологический институт – филиал НИЯУ МИФИ

Кафедра ТМ и МАХП

Лабораторная работа №5

по курсу “Энергоснабжение”

Тема « Теплопередача в теплообменнике типа «труба к трубе» »

Выполнили

Студенты гр. 1 Э-30 Д Салимуллин И.Д.

Комаров П.И.

Преподаватель Миллер М.А.

Озёрск

Цель работы: определить коэффициент теплопередачи в модели теплообменного аппарата экспериментальным и расчетным методом.

Введение:

Теплопередача — физический процесс передачи тепловой энергии от более горячего тела к более холодному либо непосредственно (при контакте), либо через разделяющую (тела или среды) перегородку из какого-либо материала. Когда физические тела одной системы находятся при разной температуре, то происходит передача тепловой энергии, или теплопередача от одного тела к другому до наступления термодинамического равновесия. Самопроизвольная передача тепла всегда происходит от более горячего тела к более холодному, что является следствием второго закона термодинамики.

Всего существует три простых (элементарных) вида передачи тепла:

· Теплопроводность

· Конвекция

· Тепловое излучение

Существуют также различные виды сложного переноса тепла, которые являются сочетанием элементарных видов. Основные из них:

· теплоотдача (конвективный теплообмен между потоками жидкости или газа и поверхностью твёрдого тела);

· теплопередача (теплообмен от горячей жидкости к холодной через разделяющую их стенку);

· конвективно-лучистый перенос тепла (совместный перенос тепла излучением и конвекцией);

· термомагнитная конвекция

Во многих теплообменных аппаратах передача тепла от одного теплоносителя к другому осуществляется через разделяющую их перегородку (стенку аппарата, стенку трубы и т.д.). Количество передаваемого тепла в единицу времени от горячего теплоносителя к менее нагретому рассчитывается по следующей формуле:

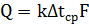Вт,

где к - коэффициент теплопередачи, Вт/(м² - град);

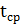- средняя разность температур (температурный напор) между теплоносителями, °С;

F-площадь теплопередающей перегородки, м².

Определив из опыта путем измерения Q, 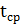, а также зная размеры теплопередающей перегородки, можно найти экспериментальный коэффициент теплопередачи:

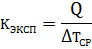
Нахождение расчетного коэффициента теплопередачи состоит из ряда последовательных вычислений.

Ход работы:

Противоток.
Теплоноситель	Горячая вода	Холодная вода
Обозначение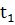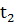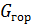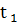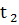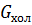
Размерность	оС	оС	делений	кг/сек	оС	оС	делений	кг/сек
№ опыта
				0,12				0,0925
сред. знач.

1.Определение экспериментального коэффициента теплопередачи.

Найдем количества тепла, отданного горячей водой за 1 секунду.

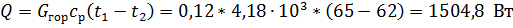
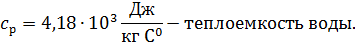
Температурный напор.

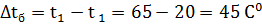
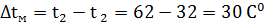Средняя температура напора.

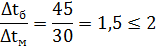
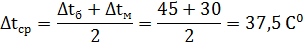
Площадь поверхности теплообменника.

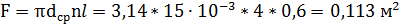
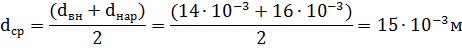
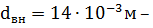внутренний диаметр внутренней трубы.

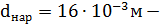наружный диаметр внутренней трубы.

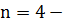число элементарных проводников.

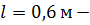длина труб.

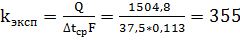Вт/(м²*град.)

2.Расчет коэффициента теплопередачи .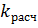

Определение коэффициента теплопередачи .

.

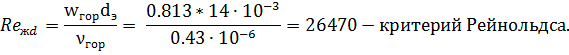
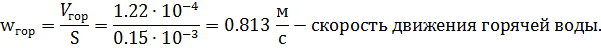
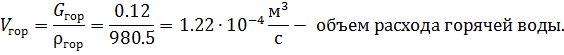
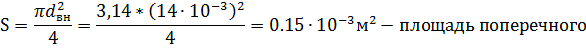
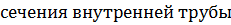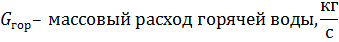
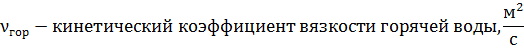
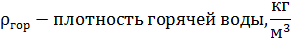
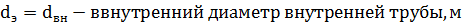
В зависимости от числа 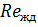находим критерий Нуссельта.

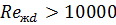=> Турбулентный режим.

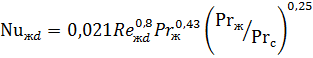
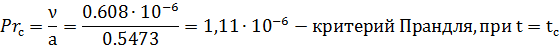
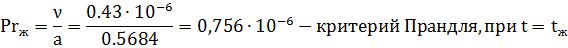
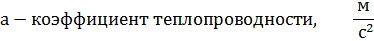
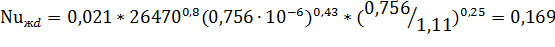
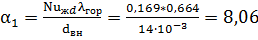Вт/(м²*град.)

Определение коэффициента теплопередачи .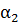

.

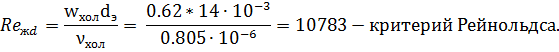
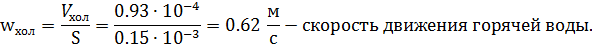
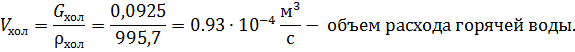
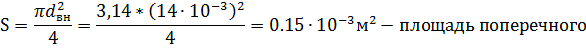
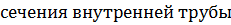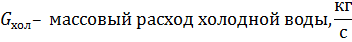
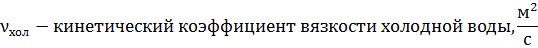
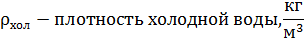
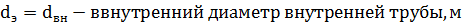
В зависимости от числа 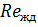находим критерий Нуссельта.

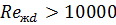=> Турбулентный режим.

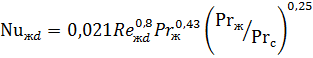
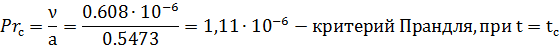
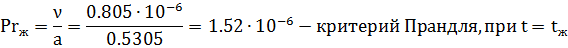
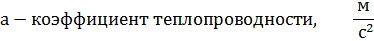
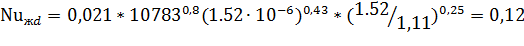
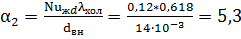Вт/(м²*град.)

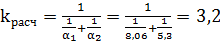Вт/(м²*град.)

Ответы на контрольные вопросы.

1. Критериальные уравнения теплоотдачи при ламинарном и турбулентном течении жидкости в трубах.

Количество теплоты, отдающееся с поверхностей нагретых частей электрических аппаратов, в основном зависит от условий конвективного теплообмена, поэтому большое значение имеет умение правильно рассчитать количество теплоты, отводимого конвекцией. Для этой цели используют критериальные уравнения, полученные на основе рассмотрения подобных явлений.
Для решения задач данного параграфа используются следующие расчетные формулы и соотношения.

Критериальное уравнение (при ламинарном и турбулентном потоке) конвективной теплоотдачи в общем виде:

Nu = ƒ(Gr, Pr, Re, Fo)

где Nu, Gr, Pr, Re и Fo - соответственно критерии Нуссельта, Грасгофа, Прандтля, Рейнольдса и Фурье

2. Критерии Nu, Re, Pr, Gr, их выражение и физическое толкование.

Число Грасгофа (Gr) — критерий подобия, определяющий процесс теплообмена при свободном движении в поле гравитации и являющийся мерой соотношения архимедовой (подъёмной) силы, вызванной неравномерным распределением плотности в неоднородном поле температур, и силами межмолекулярного трения.

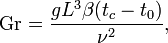
Число Прандтля (Pr) — один из критериев подобия тепловых процессов в жидкостях и газах, учитывает влияние физических свойств теплоносителя на теплоотдачу:

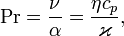
Число Прандтля — физическая характеристика среды и зависит только от её термодинамического состояния.

Число, критерий Рейнольдса (Re) — безразмерная величина, характеризующая отношение нелинейного и диссипативного членов в уравнении Навье — Стокса. Число Рейнольдса также считается критерием подобия течения вязкой жидкости.

Число Рейнольдса определяется следующим соотношением:

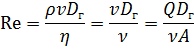
Для каждого вида течения существует критическое число Рейнольдса, Re_кр, которое, как принято считать, определяет переход от ламинарного течения к турбулентному. При 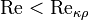течение происходит в ламинарном режиме, при 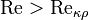возможно возникновение турбулентности. Критическое значение числа Рейнольдса зависит от конкретного вида течения (течение в круглой трубе, обтекание шара и т. п.), различными возмущениями потока, как-то изменение направленности и модуля вектора скорости потока, шероховатость стенок, близость местных сопротивлений и др.

Число Нуссельта (Nu) — один из основных критериев подобия тепловых процессов, характеризующий соотношение между интенсивностью теплообмена за счёт конвекции и нтенсивностью теплообмена за счёт теплопроводности (в условиях неподвижной среды). Названо в честь немецкого инженера Вильгельма Нуссельта:

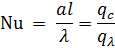
3. Среднелогарифмический напор для теплообменника типа «труба в трубе» при прямотоке и противотоке.

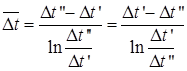или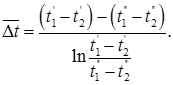

Такое значение температурного напора называется среднелогарифмическим и часто в литературе обозначается Δt_лог.

Точно таким же образом выводится формула осреднения температурного напора и для противотока. Отличие лишь в том, что в правой части уравнения (г) следует поставить знак минус, и поэтому здесьm=1/W₁ - 1/W₂. Окончательная формула для среднего логарифмического температурного напора при противотоке имеет вид:

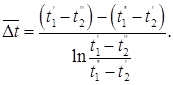
4. Физический смысл коэффициентов 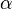и χ.

Коэффициент пропорциональности 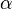— коэффициент теплоотдачи (англ.) - плотность теплового потока при перепаде температур на 1K, измеряется в Вт/(м²·К). В реальности он не всегда постоянен и может даже зависеть от разности температур, делая закон приблизительным. Если рассматривать тепловой поток как вектор, то он направлен перпендикулярно площадке поверхности, через которую протекает.

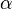— количество теплоты, отдаваемое с 1 м² поверхности за единицу времени при единичном температурном напоре. Он зависит:

· от вида теплоносителя и его температуры;

· от температуры напора, вида конвекции и режима течения;

· от состояния поверхности и направления обтекания;

· от геометрии тела.

Поэтому 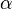— функция процесса теплоотдачи; величина расчётная, а не табличная; определяется экспериментально.

Эквивалентная запись:

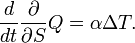
χ — коэффициент теплопроводности (иногда называемый просто теплопроводностью), отношение теплового потока dqчерез малый элемент поверхности к площади dS этой поверхности называют поверхностной плотностью теплового потока.

5. Виды движения жидкости.

Основные виды движения жидкости: равномерное и неравномерное; установившееся и неустановившееся; напорное и открытое (безнапорное); ламинарное и турбулентное.

Установившееся неравномерное движение представляет практический интерес только для открытых русел, т. к. трубопроводы обычно имеют постоянное по длине сечение, а относительно короткие переходные участки (конфузоры и диффузоры), характеризующиеся некоторыми особенностями в отношении работы трения, учитываются как местные сопротивления в основном расчетном уравнении Бернулли.

Неравномерное движение в открытом русле может быть плавноизменяющимся или относительно резкоизменяющимся. В первом случае конвективная сила инерции играет небольшую роль и зачастую ею можно пренебрегать по сравнению с силой трения, во втором случае эти силы, по меньшей мере, соизмеримы.

Значительное увеличение скорости на участке малой длины достигается в случае водосливов, перепадов, быстротоков (см. Гидравлика сооружений); такое же уменьшение скорости возможно в случае прыжка гидравлического.

Неустановившееся равномерное движение практически возможно лишь в трубах постоянного сечения. Например, в трубопроводе, питаемом поршневым насосом; в трубопроводе, подающем воду к турбине при колебаниях нагрузки ГЭС.

Перед инерционным напором ставится знак плюс, если скорость в трубе с течением времени увеличивается, и минус, если скорость уменьшается. Потерянный напор при неустановившемся движении отличается от его значений в соответствующих условиях (при одинаковых шероховатости, вязкости, скорости, диаметре) установившегося движения, причем и при положительном и при отрицательном ускорении возрастает по сравнению с установившимся движением. При турбулентном движении это возрастание невелико, при ламинарном же может оказаться существенным.

При очень большом локальном ускорении в трубах возникает особое явление, наз. гидравлическим ударом.

Неустановившееся неравномерное движение представляет практический интерес лишь для открытых русел, т. к. в трубах участки переменного сечения очень короткие и сила инерции массы жидкости, заполняющей эти участки, несущественна, но сравнению с силой инерции масс жидкости, заполняющих участки постоянного диаметра. Изменение скорости, а следовательно, и расхода с течением времени влечет за собой изменение глубины наполнения русла, причем оно происходит не синхронно но всей длине потока, а начинается на одном из его концов и затем распространяется в виде волны, волной изменения расхода и отличается от колебательных волн (ветровых, корабельных и др., см. Волны). Волны изменения расхода возникают в реках и каналах при наполнении и опорожнении камер судоходных шлюзов, при суточном колебании мощности гидроэлектростанций.