Статистическое определение вероятности события
Пусть в одинаковых условиях проводят N испытаний, в каждом из которых следят за появлением некоторого события А. Обозначим через МА – число появлений события А в N испытаниях.
Относительной частотой (или частостью) случайного события А в серии из N испытаний называется отношение числа испытаний, в которых это событие произошло, к общему числу произведенных испытаний, т.е.
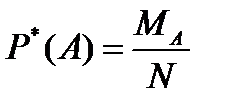(1)
При малом числе испытаний относительная частота события в значительной мере случайна. Однако при увеличении числа испытаний относительная частота событий постепенно теряет свой случайный характер. Случайные обстоятельства, сопровождающие каждое отдельное испытание, в массе испытаний взаимно погашаются, и частота постепенно стабилизируется, приближаясь с незначительными колебаниями, к некоторой постоянной величине. Естественно предположить, что эта постоянная величина и есть не что иное, как вероятность события А.
Вероятностью случайного события А называется число, около которого устойчиво колеблется относительная частота этого события, наблюдаемая при неограниченном увеличении числа испытаний.
Данное определение носит название статистического определения вероятности события.
Таким образом, частота события приближенно совпадает с его вероятностью, если число испытаний достаточно велико. Имеется огромный опытный материал по проверке этого утверждения. В качестве иллюстрации рассмотрим данные, которые относятся к примеру с бросанием монеты. Следующая таблица взята из книги Колмогорова А.Н., Журбенко И.Г. и Прохорова А.В. «Введение в теорию вероятностей» и в ней помещены результаты, экспериментально полученные различными исследователями, начиная с XVIII века:
| Экспериментатор | Число бросков монеты N | Относительная частота выпадения герба Р* |
| Бюффон | 0,507 | |
| Де Морган | 0,5005 | |
| Романовский | 0,4923 | |
| Пирсон | 0,5005 | |
| Феллер | 0,4979 |
По данным этой таблицы можно сделать вывод о том, что относительные частоты выпадения герба незначительно отклоняются от числа 0,5, т.е. можно считать, что вероятность появления герба равна 0,5.
Очевидно, что статистическое определение вероятности события мало пригодно для решения практических задач. В некоторых испытаниях, пользуясь элементарными приемами или чисто интуитивно, нетрудно указать конкретное число, характеризующее вероятность появления того или иного события. Например, на вопрос: чему равна вероятность выпадения герба при броске монеты? Почти все, не задумываясь, отвечают – 50 % или 0,5. И это верный ответ, если считать, что монета симметричная, правильной формы, а исход «монета встает на ребро» можно отбросить как практически невозможный.
Столь же легко можно получить вероятность выпадения четырех очков при броске игрального кубика –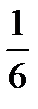 
, разумеется, с теми же оговорками насчет симметричности кубика и практической невозможности его остановке на ребре или вершине.
Рассмотрение этих примеров подводит нас вплотную к другому определению вероятности события – к классическому определению.