Аналитический метод анализа нелинейных цепей.

В предыдущем параграфе рассматривались методы расчёта нелинейных цепей при синусоидальном воздействии символическим способом путём замены несинусоидальных токов и напряжений эквивалентными синусоидами.

В ряде случаев требуется знание не только действующих значений токов и напряжений, но и их формы. Графические методы построения кривых на базе нелинейных ВАХ весьма трудоёмки и не отличаются высокой точностью.

Аналитические методы анализа нелинейных цепей требуют вывода (аппроксимации) аналитических выражений ВАХ нелинейных элементов. Как уже отмечалось, чем точнее аппроксимация, тем сложнее выражение аппроксимирующей функции, тем труднее анализ исследуемой цепи.

Поэтому на практике широкое распространение получила кусочно-линейная аппроксимация ВАХ, которая позволяет разбить весь процесс на ряд участков, на которых можно считать постоянными параметры нелинейных элементов.

Покажем применение этого метода на конкретных примерах.

Пример 8. Для цепи рис49.а рассчитать и построить кривую тока для двух случаев аппроксимации вебер-амперной характеристики индуктивной катушки с сердечником (рис.49.б,в). Соответствующие значения потокосцепления и тока даны в таблице 10.

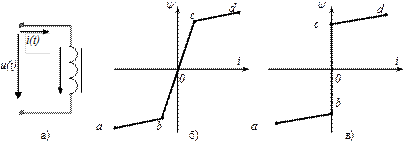
Рис.49. Аналитический расчет тока

Значения потокосцепления и тока для аппроксимации Таблица 10.

Параметры	Точка на ВАХ
рис.49.б	рис.49.в
	а	b	c	d	a	b	с	d
ψ, Вб	-1	-0,95	0,95		-0,9475	-1	0,9475
i, А	-1	-0,05	0,05			-1

Потокосцепление изменяется по закону .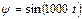

Решение. При включении идеальной катушки с сердечником на синусоидальное напряжение, потокосцепление (магнитный поток) изменяется также по синусоидальному закону, отставая от напряжения на 90⁰:

Используя рис.49.б,в и таблицу 10, определим уравнения линий аппроксимации, по формуле:

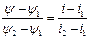, (64)

где ( 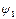, 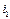); ( 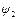, 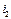) - координаты точек, через которые проходит прямая.

Для кусочно-линейной аппроксимации на рис.49.б, получим:

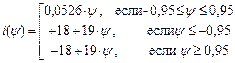. (65)

Для кусочно-линейной аппроксимации на рис.49.в:

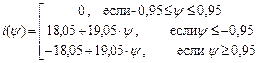. (66)

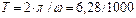Для построения формы кривой тока необходимо предварительно определить моменты времени, соответствующие точкам сопряжения линий аппроксимации (они повторяются с периодом =6,28·10^-3с):

1) точка «b» - 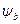=-0,95; => 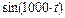=-0,95 =>t=-1,25·10^-3с, точка «с» - 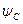=0,95; => 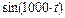=0,95 =>t=1,25·10^-3с;

2) точка «b» - 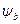=-0,9475; => 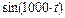=-0,9475 =>t=-1,245·10^-3с, точка «c» - 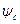=0,9475; => 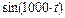=0,9475 =>t=1,245·10^-3с.

Результат расчета представлен на рис.50

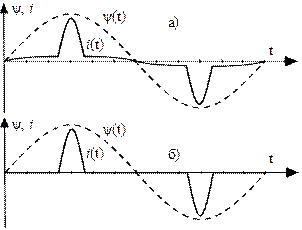
Рис.50. Форма тока для различных аппроксимаций

Пример 9. Через индуктивную катушку, зависимость 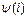которой изображена на рис49.б протекает синусоидальный ток 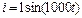. Рассчитать и построить кривую изменения напряжения на катушке .

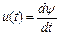Решение. Аналогично предыдущему примеру выведем зависимости 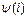для участков аппроксимации.

Для участка «bc» - 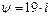, тогда напряжение на катушке:

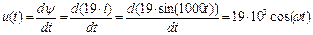. (67)

Для участка «cd» 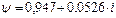, напряжение на катушке:

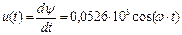. (68)

Если начать построение с 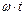=0; то расчет кривой проводится по уравнению (67) при изменении 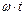от 0 до 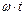= 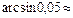0,5 рад. Далее для 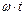от 0,5 до 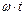= 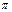-0,05=3,09рад расчет проводится по уравнению (68). Затем следует расчет по (67) и т.д. Кривая напряжения построена на рис.51.

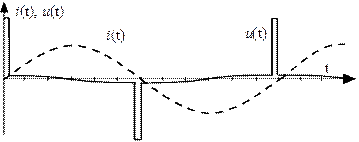
Рис.51. Форма напряжения при заданном токе

Пример 10. Рассчитать и построить зависимости , , 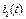, 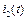для схемы на рис.52.а. ВАХ нелинейной индуктивности приведена на рис.52.б. Параметры цепи: 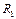= =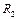100 Ом, 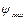=0,01 Вб; .

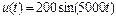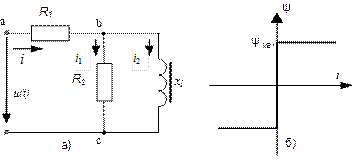
Рис.52. Разветвленная нелинейная цепь

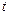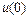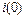Решение. Рассмотрение процессов, происходящих в цепи начнём с момента времени =0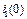, =0; =0; 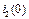=0; =0; 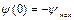. При изменении потокосцепления от 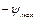до 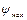ток индуктивности согласно ВАХ равен нулю ( 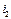=0), а токи:

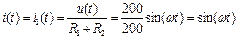. (69)

Напряжение на участке «bc» и определяется уравнением:

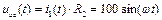. (70)

Для вывода зависимости 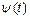воспользуемся уравнением:

,

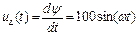из которого:

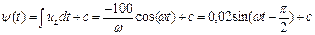, (71)

где 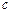– постоянная интегрирования.

Найдем постоянную интегрирования из начального условия 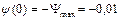Вб. Тогда из выражения (71) 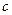=0,01.

Зависимость 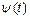принимает вид:

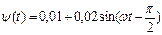. (72)

Продолжительность первого участка (перемагничивание сердечника), закончится когда 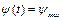, откуда

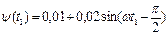=0,01 Вб, => 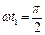. (73)

Перейдем к расчету второго участка. Согласно ВАХ характеризуется постоянством потокосцепления 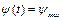=const. Тогда напряжение на участке «bc»:

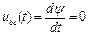. (74)

Ток через резистор 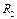: 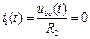. (75)

Оставшиеся токи:

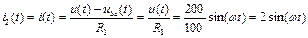. (76)

Продолжительность второго участка от 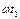до 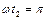. Далее всё процессы повторяются. Кривые токов и потокосцепления построены на рис.53.

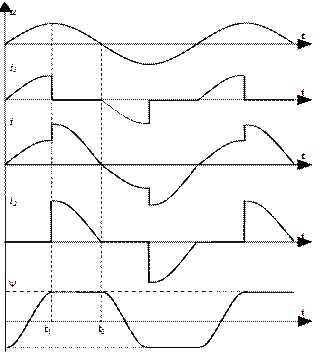
Рис.53. Расчетные кривые токов и потокосцепления

Пример 11. Построить кривые изменения во времени заряда 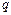, напряжения 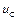на нелинейном конденсаторе и тока 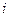в цепи, изображенной на рис.54.а, если 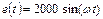, 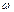=10⁵ рад/с, 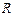=10³ Ом. Кулон-вольтная характеристика (КВХ) приведена на рис.54.б, 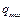=10^-5 Кл.

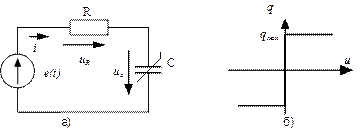
Рис.54. Разветвленная нелинейная цепь

а) схема цепи; б) Кулон-вольтная характеристика нелинейного конденсатора.

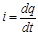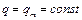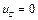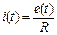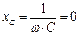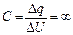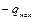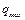Решение. Ток конденсатора, а значит и цепи определяется уравнением . На участках КВХ, когда , ток равен нулю. На вертикальном участке КВХ напряжение на конденсаторе , а ток определяется уравнением . (сопротивление конденсатора , т.к. ). Заряд на этом участке заряд изменяется от до по уравнению:

,

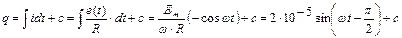где 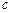-постоянная интегрирования, определяемая из начальных условий ( ):

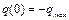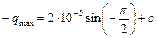, => c=10^-5 Кл.

Время перезаряда конденсатора от 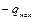до 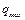определяется из последнего уравнения:

, => .

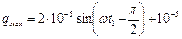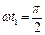Кривые тока и заряда приведены на рис.55.

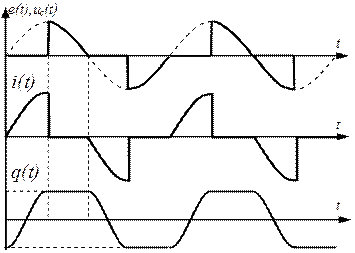
Рис.55. Кривые тока и заряда.

Пример 12. На вход схемы рис.56.а подается ток , изменяющийся по закону, заданному графиком на рис.56.б, с амплитудой

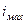=5,82∙10^-2 А и периодом Т=6,28∙10^-4с. Параметры цепи 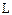=0,1465 Гн, 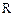=1465 Ом. КВХ нелинейного конденсатора приведена на рис.54.б ( 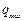=10^-6 Кл). Построить графики токов, напряжений на элементах цепи и заряда.

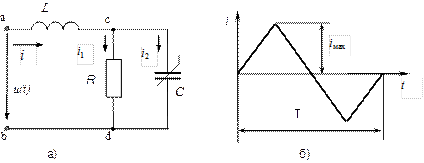Рис.55. Разветвленная нелинейная цепь

а) схема цепи; б) форма тока

Решение. Рассмотрение процесса начнем с момента 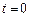, заряд конденсатора 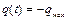. На вертикальном участке КВХ 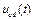=0, => 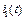=0, а 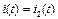. Под действием этого тока 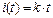, где:

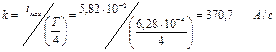
происходит перезарядка конденсатора от 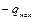до 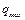по уравнению:

;

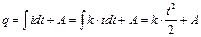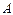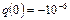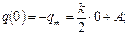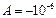где -постоянная интегрирования, определяемая из начальных условий Кл

=> Кл.

В итоге: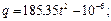

Время перезарядк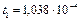и с или .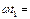

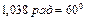Напряжение на индуктивности изменяется по закону:

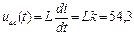В.

На горизонтальном участке КВХ (после насыщения, 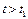) 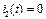, , 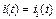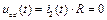Напряжение на входе цепи

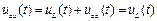
Заданные зависимости построены на рис.56

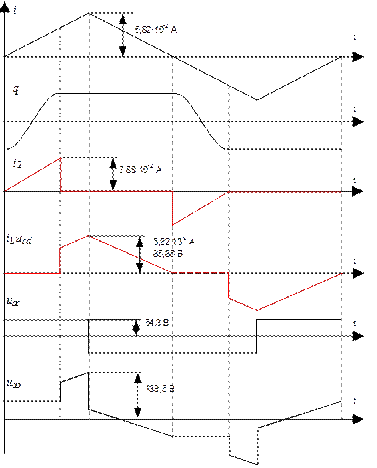
Рис.56. Кривые тока, напряжения и заряда