Способ вращения вокруг оси, параллельной плоскости проекций.

Способ вращения вокруг оси, параллельной плоскости проекций особенно широко применяется при решении четвертой задачи на преобразование чертежа, т.е. при преобразовании плоскости обще­го положения в плоскость уровня. При таком преобразовании все фигуры, лежащие в плоскости, будут проецироваться в натураль­ную величину. Особое преимущество настоящего способа преобра­зования перед ранее рассмотренными, состоит в том, что он на­иболее рационален, т.к. этот способ переводит плоскость общего положения в плоскость уровня, минуя предварительный ее перевод в плоскость проецирующую, что было необ­ходимо во всех предыдущих способах.

По этой причине задачи на определение истинных величин фигур и углов решаются преимущественно этим, способом.

Вращением около горизонтали, т. е. прямой, параллельной пло­скости p₁, найдем натуральную величину основания пирамиды - треугольника АВС.

Построение.

1.Построив в плоскости треугольника горизонталь h(C1), принима­ем ее за ось вращения.

(hÌΔАВС)Ù(h ¤¤ p₁);

Горизонтальные проекции окружностей, по которым будут пе­ремещаться вершины А и В представляют собой прямые, перпендикуляр­ные к оси вращения.(рис.12.1)

Рис.12.1

2.Находим повернутое положение вершин треуголь­ника.

Новое положение вершины В - точку В₁^/, предвари­тельно найдя способом прямоугольного треугольника натуральное значение радиуса вращения этой точки,

R = ОВ = O^/ В _о.(рис.12.2)

Рис.12.2

Вершина треугольника С, как лежащая на оси вращения, останет­ся неподвижной.

Повернутое положение вершины А найдем из двух следующих условий.

а)Горизонтальная проекция окружности, как отмечалось выше, по которой будет пе­ремещаться вершина А, представляет собой прямую, перпендикуляр­ную к оси вращения.

б) Сторона AB в повернутом положении, как и до поворота, будет проходить через точку 1. Точка 1 в процессе поворота остается неподвижной, т.к. она лежит на оси вращения. Проводим прямую через точки В^′₁, 1^′ .

Пересечение прямых, найденных из этих двух условий, дает нам новую горизонтальную проекцию повернутой вершины А - точку А^′₁.(рис.12.3)

Рис.12.3.

Соединяя вершины А^′₁,В^′₁,C^′ получаем новую горизонтальную проекцию треугольника АBС, плоскость которого параллельна плоскости p₁ . Следовательно треугольник А^′₁ В^′₁C^′ представляет со­бой натуральную величину заданного треугольника:

[DA₁^/B₁^/ C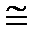^/] [DABC] (рис.12.4)

Рис.12.4.

Задача №4. Определить истинную величину ребра SC (в мм) и уголего наклона к плоскости основания пирамиды (в градусах).