Бесконечно малые функции и их свойства

Понятие предела функции, его геометрический смысл.

Односторонние пределы

Рассмотрим функцию у = f(х), определённую на некотором интервале, содержащим точку х = a.

Определение. Число А называется пределом функции у = f(х) при х, стремящемся к a (или в точке a), если для любого числа e > 0 существует такое d > 0, что при всех х, удовлетворяющих условию

0 < |x – a| < d, (1)

выполняется неравенство

|f(x) – A| < e. (2)

Обозначение: f(х) = A.

Выясним геометрический смысл этого определения, воспользовавшись графиком функции у = f(х) (см. рис. 1).

Неравенство (1) означает, что х отстоит от точки а не далее чем на d, то есть принадлежит интервалу ]a – d, a + d[ или d-окрестности точки а на оси Ох. Неравенство (2) означает, что значение функции у = f(х) не выходит из интервала ]А – e, А + e [ оси Оу, то есть принадлежит e-окрестности точки А этой оси.

Рассмотрим также односторонние пределы функции: предел слева 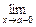f(х) = A₁ и предел справа 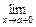f(х) = A₂. Они определяются следующим образом. A₁ и A₂ – такие числа, к которым стремится значение функции f(х) при стремлении аргумента х к а слева (справа).

Можно показать, что если односторонние пределы равны (см. рис. 1) 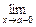f(х) = 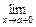f(х) = A, то предел в точке х = а существует и равен односторонним пределам f(х) = 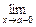f(х) = 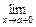f(х) = A.

Из определения предела функции следует, что предел постоянной равен этой постоянной.

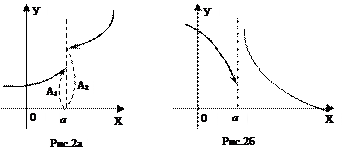
Если односторонние пределы различны (см. рис. 2.а) 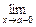f(х) ¹ 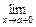f(х), то есть А₁ ¹ А₂, или хотя бы один из них не существует (см. рис. 2.б), то не существует и предел функции в точке х = а.

Сформулируем понятие предела функции, когда х неограниченно возрастает по модулю, то есть х ® ¥.

Определение. Число А называется пределом функции у = f(х) при х ® ¥, если для любого положительного числа e существует положительное число N такое, что для всех значений аргумента х, удовлетворяющих условию |x| > N, справедливо неравенство |f(x) – A| < e.

Для обозначения предела функции у = f(х) при х ® ¥ используется запись 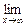f(х) = А.

Бесконечно малые функции и их свойства

Определение. Функция у = f(х) называется бесконечно малой при х ® а (или при х ® ¥), если f(х) = 0 ( 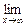f(х) = 0).

Бесконечно малую функцию аргумента х обозначают о(х).

Например, функция у = (х – 3)² есть бесконечно малая при х ® 3, так как 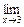(х – 3)² = 0; функция у = 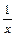является бесконечно малой при х ® ¥, поскольку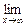 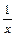= 0.

Свойства бесконечно малых функций выражаются следующими

теоремами.

Теорема 2.2.1. Если функция у = f(х) имеет предел b при х ® а,

то у(х) = b + о(х). Обратное: если у(х) = b + о(х), то f(х) = b.

Теорема 2.2.2. Алгебраическая сумма конечного числа бесконечно малых функций при х ® а есть бесконечно малая функция при х ® а.

Теорема 2.2.3. Произведение бесконечно малой на ограниченную функцию есть бесконечно малая функция.

Следствие 1. Произведение двух бесконечно малых функций есть бесконечно малая функция.

Следствие 2. Произведение бесконечно малой функции на постоянную есть бесконечно малая функция.