Понятие n-мерного пространства

Из курса аналитической геометрии известно, что всякий вектор А, расположенный на числовой оси, определяется координа­той А=(х), т. е. одним действительным числом. Прямая - одномерное векторное пространство. Всякий век­торА, расположенный на плоскости с заданной системой координат, определяется двумя координатами или компонентами: А = (х, у), т. е. упорядоченной системой из двух действительных чисел. Плоскость является двумерным векторным пространством. Всякий вектор А трехмерного векторного пространства определяется тремя координа­тами или компонентами: А = (x; у; z), т. е. упорядоченной системой из трех действительных чисел

В экономике, физике, геометрии приходится изучать объекты, для задания которых недостаточно трех действительных чисел. Пусть, например, некоторый промышленный район производит станки, хлоп­чатобумажные ткани, автомобили, телевизоры, шерстяные изделия и т. д. Для характеристики производства района, очевидно, потребует­ся упорядоченная система из n действительных чисел. Таким образом, целесообразно рассмотреть совокупности всевозможных упорядочен­ных систем из n действительных чисел.

n-мерным векторным пространством называется совокупность всевозможных упорядочен­ных систем из n действительных чисел после введения в нее операций сложения и умножения на действительное число.

n-мерным вектором А = (a₁, a₂,..., a_n) называется упорядоченная система из n действитель­ных чисел a₁, a₂,..., a_n, которые называются компо­нентами вектора А.

Векторы условимся обозначать большими буквами латинского ал­фавита, а числа - малыми. Коэффициенты всякого линейного уравне­ния с n неизвестными образуют n-мерный вектор; всякое решение системы линейных уравнений с n неизвестными – n -мерный вектор; в матрице из т строк и n столбцов строки являются n-мерными векто­рами, столбцы — m-мерными векторами и т. д.

Суммой векторов А и В называется вектор A+B=(a₁+b₁,a₂+b₂,…,a_n+b_n), компонентами которого являются суммы соответствующих компонент слагаемых векторов.

Разностью двух векторов А и В является вектор

А - В = А + (- В) или A-B=(a₁-b₁,a₂-b₂,…,a_n-b_n ).

Произведением вектора А на число k называется вектор kA =(ka₁, ka₂,..., ka_n), компоненты которого равны соответствующим компонентам вектораА,умноженным на число k.

Скалярным произведением двух век­торов А и В называется действительное число, равное сумме произве­дений соответствующих компонент этих векторов:

A+B=(a₁b₁+a₂b₂+…+a_nb_n ).

Длиной вектораА или его модулем называется действительное неотрицательное число, равное корню квадратному из суммы квадратов его компонент: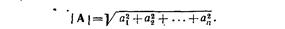

Рассмотрим линейное уравнение, содержащее n неизвестных:

a₁x₁+a₂x₂+…+a_nx_n =b.

Левая часть этого уравнения - линейная функция от n неизвестных:

Z= a₁x₁+a₂x₂+…+a_nx_n

и может быть представлена в виде скалярного произведения векторов:

Z = АХ, где А =(a₁, a₂,..., a_n) ,Х =(x₁, x ₂,..., x_n).

Линейная функция от неизвестных x₁, x₂,..., x_n вполне определяется вектором А из своих коэффициентов, и, наоборот, всякий n-мерный вектор однозначно определяет некоторую линейную функцию. Исходя из этого, сложение и умножение вектора на число превращаются в соответствующие операции над линейными функциями, которые ши­роко используются при решении задач линейного программирования.