Анализ и обработка результатов измерений. 1. По данным табл. 11.1 постройте график зависимости l = f (N).
1. По данным табл. 11.1 постройте график зависимости l = f (N).
Градуировочный график l = f (N) строится по среднему значению <N> этих двух измерений. По оси ординат откладывают длины волн, а по оси абсцисс – деления барабана. Выбирая масштаб графика, помните, что миллиметровая бумага даёт возможность точно задать три значащие цифры. Эту возможность Вы должны использовать! Строя график, не заканчивайте кривую на последней точке, а плавно проводите её в область бóльших длин волн. Для этого, выбирая масштаб по оси ординат, проставьте запасные деления вплоть до 650–700 нм, и соответствующие им деления по оси абсцисс.
2. На градуировочном графике для трех длин волн, указанных преподавателем, определите угловой коэффициент касательных, сделайте вывод о характере дисперсии света в изученном диапазоне длин волн.
3. Пользуясь градуировочным графиком, определите длину волны, соответствующую каждой линии в спектре газоразрядной трубке, исследование которой было проведено во втором задании. Полученные значения впишите в таблицу 6.2.
4. Найдите в литературе значение длин волн, соответствующие линиям в спектре атомарного водорода, зарисуйте спектр водорода, нанеся каждую линию на ось l с соблюдением масштаба и цвета линии излучения.
Контрольные вопросы
1. Дайте определение: спектра излучения, монохроматора, линейчатого и сплошного спектра, постулатов Бора.Письменный ответ на этот вопрос необходимо включить в отчет.
2. Назовите составные части лабораторной установки и их назначение.
3. Какие величины измеряются в данной работе непосредственно? Какие вычисляются?
4. Опишите характерные особенности линейчатого и сплошного спектров. Чем излучается тот и другой?
5. Какой газ будет использован Вами для градуировки монохроматора?
6. Почему в лампе дневного света Вы видите наложение сплошного и линейчатого спектров?
7. Что такое дисперсия света, какая природа этого явления? Какие виды дисперсии вы знаете?
8. Как зависит полная энергия электрона в атоме водорода от номера орбиты?
9. Каково соотношение между потенциальной, кинетической и полной энергиями электрона в атоме водорода?
10.Как изменяются полная и кинетическая энергия электрона при излучении кванта?
Работа № 12. ИЗУЧЕНИЕ ЗАКОНОВ ВНЕШНЕГО ФОТОЭФФЕКТА
Цель работы: ознакомится с явлением фотоэффекта, снять вольтамперную характеристику фотоэлемента, экспериментально определить количество, скорость и энергию выбитых из вещества электронов, граничную частоту фотоэффекта для данного фотоэлемента.
Оборудование: оптическая скамья, лампа накаливания, фотоэлемент, набор оптических фильтров, блок питания с встроенными микроамперметром и вольтметром.
Краткая теория
Фотоэффект — это испускание электронов веществом под действием электромагнитного излучения. В конденсированных веществах (твёрдых и жидких) выделяют внешний и внутренний фотоэффект.
Внешним фотоэффектом (фотоэлектронной эмиссией) называется испускание электронов веществом под действием электромагнитных излучений. Электроны, вылетающие из вещества при внешнем фотоэффекте, называются фотоэлектронами, а электрический ток, образуемый ими при упорядоченном движении во внешнем электрическом поле, называется фототоком.
Внутренним фотоэффектом называется перераспределение электронов по энергетическим состояниям в твёрдых и жидких полупроводниках и диэлектриках, происходящее под действием излучений. Он проявляется в изменении концентрации носителей зарядов в среде - увеличении электрической проводимости вещества под действием излучения.
В 1839 году Александр Беккерель наблюдал явление фотоэффекта в электролите. В 1873 году Уиллоуби Смит обнаружил, что селен является фотопроводящим, что обусловлено протеканием фотоэффекта. В 1887 году Генрихом Герцем при работе с открытым резонатором заметил, что при освещении ультрафиолетом цинковых разрядников прохождение искры заметно улучшается. Официально считается, что явление внешнего фотоэффекта было открыто в 1888 г. Г. Герцем.
Русский физик Александр Столетов в 1888—1890 годах, изучая фотоэффект, сделал несколько важных открытий в этой области, в том числе вывел первый закон внешнего фотоэффекта.
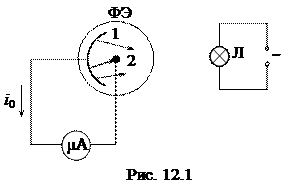 Для наблюдения внешнего фотоэффекта можно использовать вакуумный фотоэлемент. Такой фотоэлемент, независимо от его типа, состоит из двух электродов, один из которых, катод, выполнен из металла с небольшой работой выхода электронов А, например цезия. При освещении светом такого металла электроны сравнительно легко вырываются с его поверхности. Второй электрод – анод – вводится для того, чтобы принять эти электроны и, благодаря возникшему току, зафиксировать их наличие. Катод и анод помещаются в стеклянный вакуумированный баллон. Источник света – лампа накаливания Л, подключённая к источнику переменного напряжения. Для измерения тока в этом простейшем случае достаточна установка, не содержащая источника питания (рис. 12.1).
Для наблюдения внешнего фотоэффекта можно использовать вакуумный фотоэлемент. Такой фотоэлемент, независимо от его типа, состоит из двух электродов, один из которых, катод, выполнен из металла с небольшой работой выхода электронов А, например цезия. При освещении светом такого металла электроны сравнительно легко вырываются с его поверхности. Второй электрод – анод – вводится для того, чтобы принять эти электроны и, благодаря возникшему току, зафиксировать их наличие. Катод и анод помещаются в стеклянный вакуумированный баллон. Источник света – лампа накаливания Л, подключённая к источнику переменного напряжения. Для измерения тока в этом простейшем случае достаточна установка, не содержащая источника питания (рис. 12.1).
При освещении фотоэлемента электроны вылетают из катода и, обладая кинетической энергией, будут удаляться от катода и могут случайно попасть на анод, создав в цепи фотоэлемента ток. Этот ток i0будет мал, ибо большинство электронов, выбитых с поверхности катода, движутся произвольно и на анод почти не попадают.
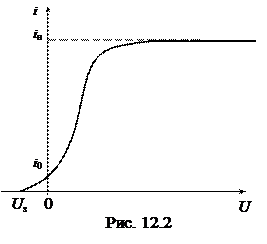 Фототок можно увеличить, если подать на фотоэлемент напряжение, которое заставит выбитые электроны менять случайное направление своего движения и двигаться к аноду. Чем большее напряжение подано на фотоэлемент, тем большее число электронов примет участие в направленном движении и тем больше будет фототок. Число притянутых электронов, а значит и ток, с увеличением напряжения U на фотоэлементе будут возрастать до тех пор, пока в направленном движении не примут участие все выбитые светом электроны. Дальнейшее увеличение напряжения не приведёт более к возрастанию тока – будет достигнут ток насыщения iн (рис. 12.2). График зависимости силы тока от напряжения на фотоэлементе, изображённый на рис. 3.2, называют вольтамперной характеристикой фотоэлемента.
Фототок можно увеличить, если подать на фотоэлемент напряжение, которое заставит выбитые электроны менять случайное направление своего движения и двигаться к аноду. Чем большее напряжение подано на фотоэлемент, тем большее число электронов примет участие в направленном движении и тем больше будет фототок. Число притянутых электронов, а значит и ток, с увеличением напряжения U на фотоэлементе будут возрастать до тех пор, пока в направленном движении не примут участие все выбитые светом электроны. Дальнейшее увеличение напряжения не приведёт более к возрастанию тока – будет достигнут ток насыщения iн (рис. 12.2). График зависимости силы тока от напряжения на фотоэлементе, изображённый на рис. 3.2, называют вольтамперной характеристикой фотоэлемента.
Если сменить знаки на электродах и подать небольшой отрицательный потенциал на анод, то электроны, выбитые светом, уже не будут ускоряться тем электрическим полем, в которое они попадают. Наоборот, поле будет их задерживать, так как анод будет отталкивать фотоэлектроны, испущенные катодом. Ток станет меньше i0, но не прекратится, поскольку выбитые электроны, благодаря полученной от света кинетической энергии, будут двигаться против поля и некоторые из них смогут достичь анода. Только при определённом значении обратного напряжения, когда кинетическая энергия даже самых быстрых электронов будет вся расходоваться на работу против сил поля, ток в цепи фотоэлемента станет равным нулю: это минимальное значение обратного напряжения, при котором фототок становится равным нулю, называют запирающим (или задерживающим) напряжением Uз .Очевидно, что запирающее напряжение пропорционально максимальной кинетической энергии электронов:
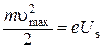 . . | (12.1) |
Измерив Uз , можно определить максимальные значения кинетической энергии и скорости фотоэлектронов.
Экспериментальные исследования, выполненные в конце XIX в., выявили следующие закономерности внешнего фотоэффекта.
1. При неизменном спектральном составе электромагнитных излучений, падающих на фотокатод, фототок насыщения прямо пропорционален энергетической освещенности катода (иначе: число фотоэлектронов, выбиваемых из катода за 1 с, прямо пропорционально интенсивности подающего на него излучения). Этот закон называют законом Столетова.
2. Максимальная начальная скорость фотоэлектронов не зависит от интенсивности падающего света, а определяется только его частотой.
3. Для каждого фотокатода существует красная граница фотоэффекта, то есть минимальная частота электромагнитного излучения ν0 (максимальная длина волны), при которой фотоэффект ещё возможен.
В фотоэффекте проявляется квантовая природа света. Объяснить закономерности фотоэффекта, используя волновую точку зрения на свет нельзя.
Запишем для фотоэффекта закон сохранения энергии. Свет, падая на металл, расходует свою энергию W на два процесса: выбивание электронов с поверхности катода (совершение работы выхода А) и сообщение электронам кинетической энергии
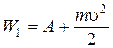 . . | (12.2) |
Согласно сформулированных Максвеллом классическим волновым представлениям о свете, в левой части равенства стоит энергия световой волны, которая, как известно, равна сумме энергий электрического и магнитного полей, комбинацией которых и является световая волна:
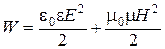 . . | (12.3) |
Увеличение световой энергии, вызванное, например, приближением источника света, должно привести, как это следует из (3.1), к увеличению скорости выбитого электрона, так как работа выхода А является постоянной для данного металла величиной и определяется свойствами самого металла. Следовательно, максимальная скорость выбитых электронов должна зависеть от интенсивности света, так как интенсивность, по определению, равна средней энергии W, проходящей через единицу площади за единицу времени:
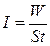 , , | (12.4) |
где S – площадь освещаемой поверхности, t – время.
Но! Из формулировки второго закона фотоэффекта следует, что скорость электронов зависит не от интенсивности, а от частоты света.
Кроме того, волновые представления о свете приводят к тому, что свет любой частоты, обладая достаточной интенсивностью, должен вызывать фотоэффект. На опыте же наблюдается ситуация, когда свет с частотой меньше некоторой минимальной, вообще не вызывает фотоэффекта, даже при очень большой интенсивности (закономерность 3).
Таким образом, видно, что волновые представления о свете не позволяют полностью объяснить явление фотоэффекта.
Объяснение фотоэффекта оказывается возможным на базе не волновых, а квантовых представлений о свете. Такую замену в 1905 г. предложил Альберт Эйнштейн. С точки зрения квантовых представлений энергию света W следует считать энергией потока квантов света – фотонов. Если каждый фотон обладает энергией hn (h – постоянная Планка, n – частота света), то поток фотонов несёт энергию
| W = N hn, | (12.5) |
где N – число фотонов. В этом случае увеличение количества фотонов приводит к увеличению интенсивности света, а увеличение частоты – к увеличению энергии отдельного фотона.
Эйнштейн предположил, что каждый электрон выбивается отдельным фотоном, поэтому в законе сохранения энергии (3.2) в случае фотоэффекта нужно учитывать не всю энергию света, а лишь энергию одного кванта. Записанный таким образом закон сохранения энергии носит название уравнения Эйнштейна для фотоэффекта:
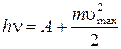 . . | (12.6) |
Таким образом, согласно квантовой теории излучения энергия фотона расходуется на выбивание электрона и ещё на сообщение ему кинетической энергии.
Закономерности фотоэффекта, описанные выше, прекрасно объясняются квантовой теорией света. Действительно, раз интенсивность света пропорциональна числу фотонов и для выбивания одного электрона нужен один фотон, то увеличение интенсивности приводит к увеличению количества выбитых электронов и, следовательно, фототока (закономерность 1). Согласно определению силы тока (i= Dq/Dt) наибольшее значение фототока должно быть прямо пропорционально числу N всехэлектронов, выбитых светом из катода за одну секунду:
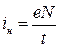 . . | (12.7) |
Из уравнения Эйнштейна (3.6) видно, что максимальная кинетическая энергия фотоэлектронов прямо пропорциональна частоте света и, соответственно, их скорость также возрастает с увеличением частоты (закономерность 2). Если же частота света будет меньше некоторой минимальной частоты n0, такой что
| hn0 = A, | (12.7) |
то фотоэффект происходить не будет, так как энергия фотона меньше работы выхода: энергии фотона не хватит на то, чтобы выбить электрон (закономерность 3).
Описание установки
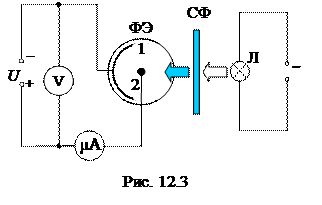 Внешний фотоэффект изучают на установке, состоящей из фотоэлемента и лампы накаливания, размещаемых на оптической скамье, а также цифровых микроамперметра и вольтметра, конструктивно объединенных вместе с реостатом в один электронный блок приборов. Электрическая схема установки представлена на рис. 12.3.
Внешний фотоэффект изучают на установке, состоящей из фотоэлемента и лампы накаливания, размещаемых на оптической скамье, а также цифровых микроамперметра и вольтметра, конструктивно объединенных вместе с реостатом в один электронный блок приборов. Электрическая схема установки представлена на рис. 12.3.
Вакуумный фотоэлемент ФЭ заключён в защитный кожух с окном и представляет собой стеклянный баллон, половина которого изнутри покрыта тонким слоем щелочного металла. Этот слой является катодом фотоэлемента. Анодом служит металлическое кольцо, расположенное в центре баллона.
Источником света является галогеновая лампа накаливания Л, напряжение на которой, а значит и интенсивность её свечения, можно регулировать. Монохроматическое излучение получают с помощью светофильтров СФ, закрепленных во вращающейся оправе (длины волн излучения, пропускаемого светофильтрами, указаны на оправе).
Фототок измеряют цифровым микроамперметром. Напряжение на фотоэлементе может изменяться вращением ручки реостата и измеряется цифровым вольтметром. Для переключения режимов задерживающего и ускоряющего напряжений служит специальный переключатель полярности «Задерживающее – Ускоряющее».
Выполнение измерений
Задание 1. Снятие вольтамперной характеристики фотоэлемента
Для получения вольтамперной характеристики на оптической скамье следует расположить источник света, набор светофильтров и фотоэлемент как можно ближе друг к другу.
Замеры фототока нужно сделать при красном светофильтре. Устанавливая значения напряжения от 0 до 18 В (или предельно возможного на данной установке), проведите измерения силы тока и занесите результаты в табл. 12.1.
Таблица 12.1
| l = нм | |||||||||||
| Напряжение U, B | |||||||||||
| Фототок I, мкА |
Значение фототока 0 А в таблице соответствует задерживающему напряжению. Для его измерения необходимо переключить тумблер на корпусе блока питания в положение «Задерживающее», определить задерживающее напряжение, при котором фототок становится равным 0) и записать результат в первую графу табл. 12.1.
Задание 2. Изучение зависимости запирающего напряжения от частоты света
На оптической скамье снова расположите источник света, набор светофильтров и фотоэлемент как можно ближе друг к другу. Установив тумблер на корпусе блока питания в положение «Задерживающее», для данного фильтра тщательно замерьте то минимальное напряжение, при котором фототок становится равным нулю. Измерения необходимо провести три раза для каждого светофильтра. Не забудьте записать длину волны l пропускания светофильтров, указанную на их оправе. Занесите полученные результаты в табл. 12.2 и используйте при построении графика зависимости величины модуля запирающего напряжения от частоты света êUзú = f (n).
Таблица 12.2
| Цвет светофильтра | |||||||
| Длина волны l, нм | |||||||
| Частота n, ´1014 Гц | |||||||
| Запирающее напряжение Uз, В | |||||||
Средний 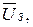 В В |
