Рассмотрим графический метод решения задачи линейного программирования.
Этот метод подходит только для задач с двумя искомыми переменными. Модель, построенная выше, будет использована для демонстрации метода.
Оси на графике представляют собой две искомые переменные (рис. 2). Не имеет значения, какую переменную отложить вдоль, какой оси. Важно выбрать масштаб, который в конечном итоге позволит построить наглядную диаграмму. Поскольку обе переменные должны быть неотрицательными, рисуется только I-й квадрант.
Рис. 2. Оси графика линейного программирования
Рассмотрим, например, первое ограничение: 3 * х1 + 10 * х2 ≤ 330. Это неравенство описывает область, лежащую ниже прямой: 3 * х1 + 10 * х2 = 330. Эта прямая пересекает ось х1 при значении х2 = 0, то есть уравнение выглядит так: 3 * х1 + 10 * 0 = 330, а его решение: х1 = 330 / 3 = 110
Аналогично вычисляем точки пересечения с осями х1 и х2 для всех условий-ограничений:
| Область допустимых значений | Граница допустимых значений | Пересечение с осью х1 | Пересечение с осью х2 |
| 3*х1 + 10*х2 ≤ 330 | 3*х1 + 10* х2 = 330 | х1 = 110; х2 = 0 | х1 = 0; х2 = 33 |
| 16*х1 + 4*х2 ≤ 400 | 16* х1 + 4*х2 = 400 | х1 = 25; х2 = 0 | х1 = 0; х2 = 100 |
| 6*х1 + 6 * х2 ≤ 240 | 6* х1 + 6 * х2 = 240 | х1 = 40; х2 = 0 | х1 = 0; х2 = 40 |
| х2 ≥ 12 | х2 = 12 | не пересекает; идет параллельно оси х1 | х1 = 0; х2 = 12 |
Графически первое ограничение отражено на рис. 3.
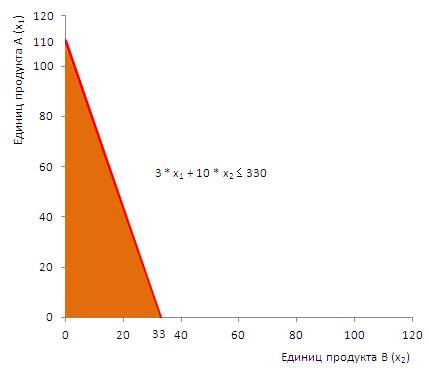
Рис. 3. Построение области допустимых решений для первого ограничения
Любая точка в пределах выделенного треугольника или на его границах будет соответствовать этому ограничению. Такие точки называются допустимыми, а точки за пределами треугольника называются недопустимыми.
Аналогично отражаем на графике остальные ограничения (рис. 4). Значения х1 и х2 на или внутри заштрихованной области ABCDE будут соответствовать всем ограничениям модели. Такая область называется областью допустимых решений.
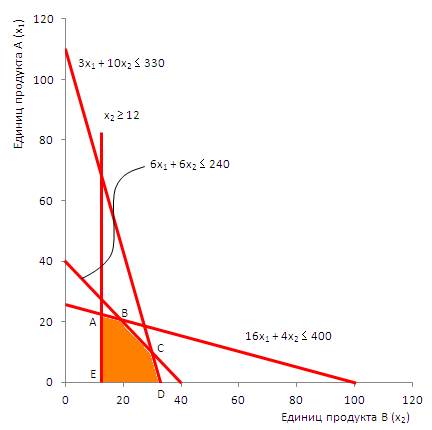
Рис. 4. Область допустимых решений для модели в целом
Теперь в области допустимых решений необходимо определить значения х1 и х2, которые максимизируют Z. Для этого в уравнении целевой функции:
Z = 2500 * х1 + 3500 *х2
разделим (или умножим) коэффициенты перед х1 и х2 на одно и тоже число, так чтобы получившиеся значения попали в диапазон, отражаемый на графике; в нашем случае такой диапазон – от 0 до 120; поэтому коэффициенты можно разделить на 100 (или 50):
Z = 25х1 + 35х2
затем присвоим Z значение равное произведению коэффициентов перед х1 и х2 (25 * 35 = 875):
875 = 25х1 + 35х2
и, наконец, найдем точки пересечения прямой с осями х1 и х2:
| Уравнение целевой функции | Пересечение с осью х1 | Пересечение с осью х2 |
| 875 = 25х1 + 35х2 | х1 = 35; х2 = 0 | х1 = 0; х2 = 25 |
Нанесем это целевое уравнение на график аналогично ограничениям (рис. 5):
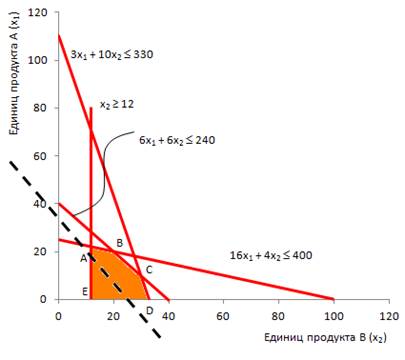
Рис. 5. Нанесение целевой функции (черная пунктирная линия) на область допустимых решений
Значение Z постоянно на всем протяжении линии целевой функции. Чтобы найти значения х1 и х2, которые максимизируют Z, нужно параллельно переносить линию целевой функции к такой точке в границах области допустимых решений, которая расположена на максимальном удалении от исходной линии целевой функции вверх и вправо, то есть к точке С (рис. 6).
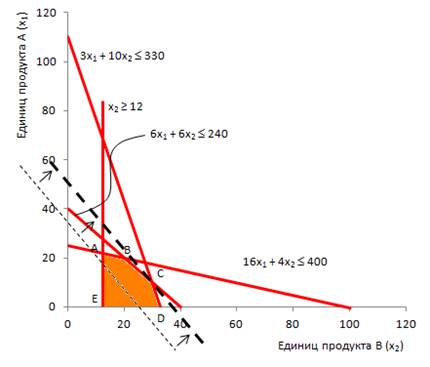
Рис. 6. Линия целевой функции достигла максимума в пределах области допустимых решений (в точке С)
Можно сделать вывод, что оптимальное решение будет находиться в одной из крайних точек области принятия решения. В какой именно, будет зависеть от угла наклона целевой функции и от того, какую задачу мы решаем: максимизации или минимизации. Таким образом, не обязательно чертить целевую функцию – все, что необходимо, это определить значения х1 и х2 в каждой из крайних точек путем считывания с диаграммы или путем решения соответствующей пары уравнений. Найденные значения х1 и х2 затем подставляются в целевую функцию для расчета соответствующей величины Z. Оптимальным решением является то, при котором получена максимальная величина Z при решении задачи максимизации, и минимальная – при решении задачи минимизации.
Определим, например значения х1 и х2 в точке С. Заметим, что точка С находится на пересечении линий: 3х1 + 10х2 = 330 и 6х1 + 6х2 = 240. Решение этой системы уравнений дает: х1 = 10, х2 = 30. Результаты расчета для всех вершин области допустимых решений приведены в таблице:
| Точка | Значение х1 | Значение х2 | Z = 2500х1 + 3500х2 |
| А | 97 000 | ||
| В | 120 000 | ||
| С | 130 000 | ||
| D | 115 500 | ||
| E | 42 000 |
Таким образом, Николай Кузнецом должен запланировать на следующий месяц производство 10 изделий А и 30 изделий В, что позволит ему получить маржинальную прибыль в размере 130 тыс. руб.
Кратко суть графического метода решения задач линейного программирования можно изложить следующим образом:
1. Начертите на графике две оси, представляющие собою два параметра решения; нарисуйте только I-й квадрант.
2. Определите координаты точек пересечения всех граничных условий с осями, подставляя в уравнения граничных условий поочередно значения х1 = 0 и х2 = 0.
3. Нанести линии ограничений модели на график.
4. Определите на графике область (называемую допустимой областью принятия решения), которая соответствует всем ограничениям. Если такая область отсутствует, значит, модель не имеет решения.
5. Определите значения искомых переменных в крайних точках области принятия решения, и в каждом случае рассчитайте соответствующее значение целевой переменной Z.
6. Для задач максимизации решение – точка, в которой Z максимально, для задач минимизации, решение – точка, в которой Z минимально.
