Задача 2. закон сохранения импульса

(количества движения точки)

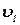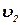Два сферических тела движутся вдоль оси х. Положительное направление оси х: слева – направо. Тело 1 находится правее, чем тело 2. В таблице 1 приведены массы и скорости тел. Скорости тел и таковы, что через некоторое время наступает соударение.

Определить скорость тел после соударения 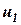и 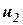для трех случаев:

1 удар тел абсолютно неупругий (пластический, то есть коэффициент восстановления );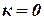

2 удар абсолютно упругий, ;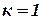

3 удар упруго-пластический, .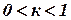

Таблица 3 - Исходные данные

Предпоследняя цифра шифра	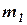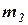, кг	, кг	Последняя цифра шифра	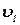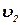, м/с	, м/с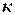
						0,6
						0,4
				-5		0,3
				-4		0,8
						0,2
				-1		0,5
						0,4
				-2		0,3
						0,6
				-3		0,7

Указания. Задача решается с использованием теоремы о сохранении количества движения системы. Два тела системы массой и не испытывают никаких силовых воздействий со стороны тел, не входящих в данную систему. Силы взаимного действия во время соударения являются внутренними, а такие силы не могут изменить количество движения системы, то есть выполняется закон сохранения количества движения системы.

Записав уравнение этого закона, получим для абсолютно пластического удара, когда после удара оба тела движутся вместе, одно алгебраическое уравнение. Это уравнение содержит одно неизвестное ( - скорость движения тел после удара: ). Решение уравнения, то есть определение значения , является решением задачи.

Если же удар не является абсолютно пластическим, то скорость тел после удара различна: 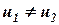. В таком случае одно уравнение закона о сохранении количества движения будет содержать два неизвестных: 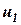и 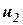. Вторым уравнением в этом случае будет являться формула для коэффициента восстановления 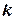для случая взаимного соударения двух тел:

.

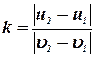(14)

В этой формуле в правой части все величины – алгебраические, то есть могут принимать положительные и отрицательные значения.

Пример 2

Условие задачи. Два тела, масса которых 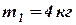, 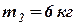движутся вдоль прямой х. Ось х направлена вправо, тело 1 находится правее тела 2. Скорости тел 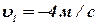, 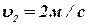. Коэффициент восстановления при соударении 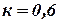(удар упруго-пластический).

Определить скорости первого и второго тел после соударения 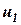и .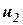

Решение

Изобразим ось х и тела 1, 2 с векторами их скоростей до соударения 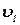и 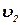. Векторы скоростей изобразим в одинаковом масштабе (рисунок 3).

При отсутствии внешних воздействий выполняется теорема о сохранении количества движения системы:

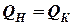(1)

где 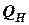- количество движения системы до удара (начальное), (кг·м)/с;

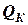- то же после удара (конечное), (кг·м)/с.

Рисунок 3 – Расчетная схема

Количество движения системы до соударения вычисляется по формуле:

,

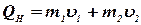(15)

после соударения

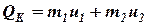(16)

Тогда уравнение (1) можно записать так:

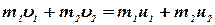(17)

Это уравнение содержит две неизвестные величины: 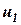и 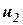. Поэтому запишем в качестве второго уравнения формулу (14) для коэффициента восстановления :

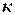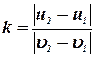По условию задачи 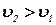, а после удара обязательно .

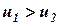С учетом этого уравнение (5) будет записано без знака модуля, и вместе с уравнением (4), оно образует систему уравнений:

.

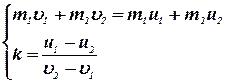(18)

Решая систему уравнений (в расчетно-графической работе необходимо привести решение), получаем , .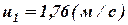

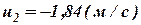Результаты расчетов и исходные данные сведем в таблице 4.

Таблица 4 – Результаты расчета

Параметры	До удара	После удара
Обозначение	Численное значение	Обозначение	Численное значение
Скорость, м/с		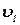-4		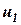1,76
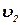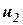			-1,84
Количество движения, кг·м/с		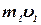-16		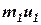7,04
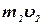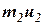			-11,04
Количество движения системы кг·м/с		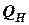-4		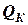-4

ЗАДАЧА 3. Принцип даламбера

Груз, подвешенный на нити, раскручивает барабан, состоящий из нескольких различных по форме и размерам деталей. Плотность материала всех деталей одинакова: 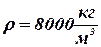(таблица 5).

Детали – однородные цилиндрические тела или стержни с прямоугольным сечением. Размеры деталей приведены в таблице 6 и определять их нужно следующим образом. Максимальный диаметр цилиндрической детали D₁. Если эта деталь полая, то внутренний диаметр – d₁. В тех вариантах, где имеется второе цилиндрическое тело, ось симметрии которого также совпадает с осью вращения барабана, то диаметр его D₂.

Таблица 5 – Варианты расчетных схем (номер варианта соответствует предпоследней цифре шифра)

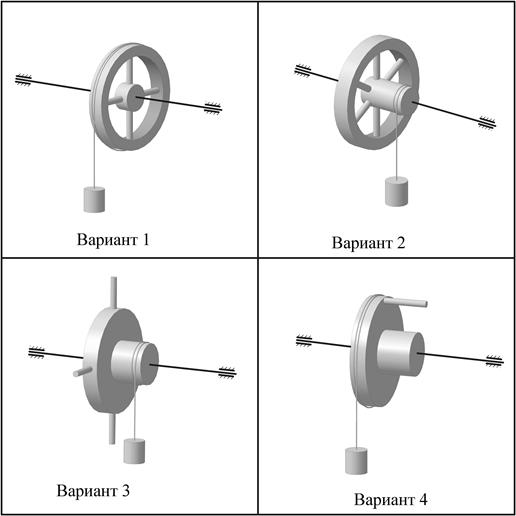
Продолжение таблицы 5

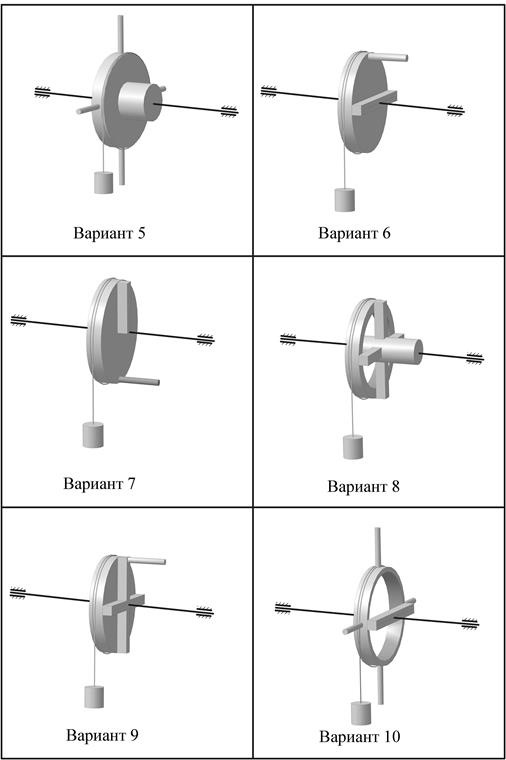
Цилиндрические детали в виде спицы колеса, в виде ручки (рукоятки) маховика или ручки «штурвала» имеют диаметр D₃. Длина таких деталей H₃ определяется размерами соседних (сопряженных) деталей (варианты 1,2 таблицы). Если этого нельзя сделать, то значение H₃ принимается из таблицы 6 (варианты 3-10).

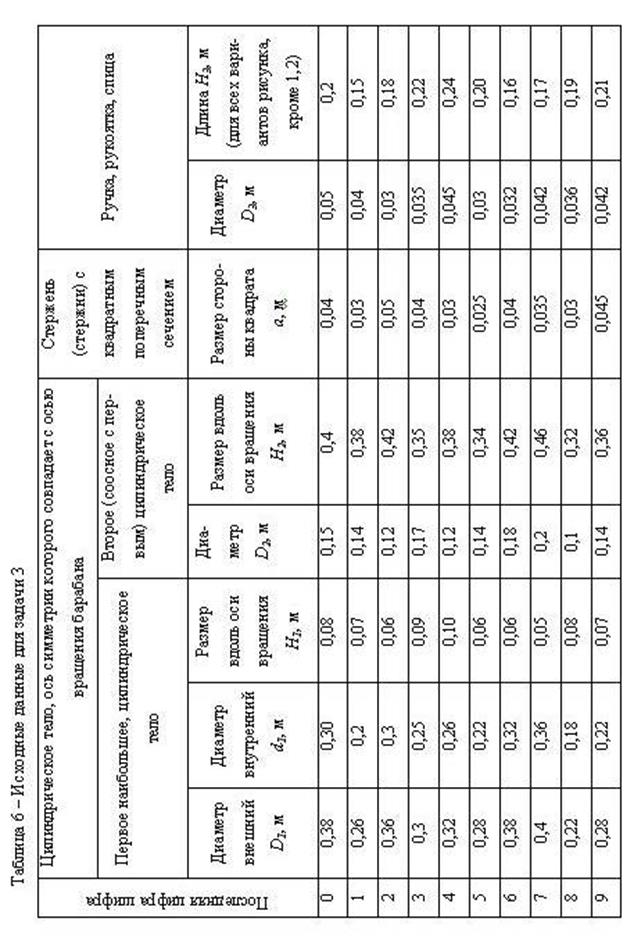
Масса груза m_г, подвешенного на нити, для всех вариантов равна 80 кг.

В задаче требуется определить ускорение груза a и угловое ускорение барабана e.

Пример 3

Условие задачи. Для примера рассмотрим вариант 0, рисунок 10. Заданные параметры: наружный диаметр первого тела D₁ = 0,38 м, внутренний диаметр первого тела d₁ = 0,3 м, размер вдоль оси вращения H₁ = 0,08 м, размер стержня с квадратным поперечным сечением а = 0,04 м, диаметр рукоятки D₃ = 0,05 м, длина рукоятки H₃ = 0,2 м, плотность материала всех деталей 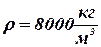, масса груза m_г = 80 кг.

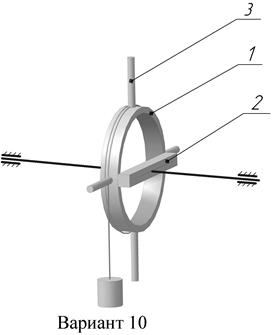
Рисунок 4 – Схема варианта

Решение

Решение задачи приведем без численных вычислений для того, чтобы не загромождать алгоритм решения. Изобразим две чертежных проекции тела, представленного на рисунке 4, и нанесем все необходимые размеры (рисунок 5).

Для определения момента инерции тела 1 относительно оси вращения I_1O выполним некоторые предварительные вычисления.

Объем 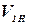сплошного цилиндра с наружным диаметром D₁ и длиной H₁ определим по формуле:

.

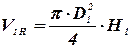(19)

Тогда его масса

.

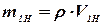(20)

Точно так же объем внутреннего цилиндра 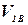с размерами d₁, H₁ определим по формуле:

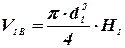(21)

Масса его .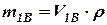

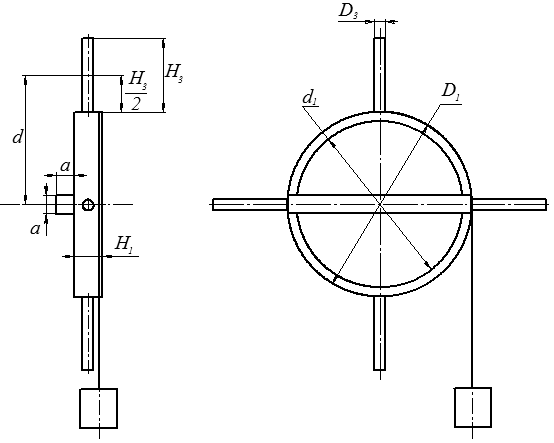
Рисунок 5 – Геометрические характеристики барабана

Момент инерции тела 1, образованного «вычитанием» из сплошного цилиндра с размерами D₁, Н₁ сплошного цилиндра с размерами d₁, H₁, вычислим по формуле:

,

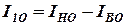(22)

где I_HO – момент инерции сплошного цилиндра с размерами D₁, Н₁, кг×м²;

I_BO – то же с размерами d₁, H₁, кг×м².

Вычислим значения I_HO и I_BO по формулам:

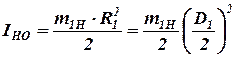;	(23)
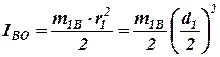.	(24)

Момент инерции тела 2 относительно оси вращения О-О определим, используя длину стержня D₁, размеры поперечного квадратного сечения а×а, по известной формуле:

,

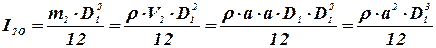(25)

где m₂ – масса тела 2, кг;

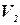- объем тела 2, м³.

Момент инерции тела 3 относительно оси О-О определяем с использованием теоремы Гюйгенса:

,

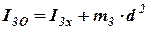(26)

где I_3X – момент инерции стержня 3 относительно оси х-х параллельной оси О-О и проходящей через центр тяжести тела 3, точку С, кг×м²;

m₃ – масса стержня 3 (вычисляется с использованием формул (1), (2)), кг;

d – расстояние между осями х и О, м.

Вычислим

.

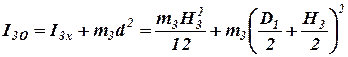(27)

Теперь момент инерции всего вращающегося тела, состоящего из тел 1, 2 и четырех стержней, вычислим по выражению:

.

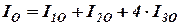(28)

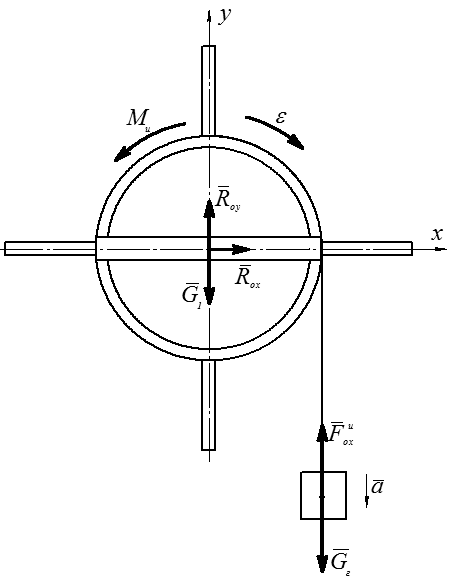
Рисунок 6 – Расчетная схема

Система состоит из двух тел: груза, весом 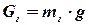и составного барабана, весом G₁. Эти силы, а также силы реактивные R_oy и R_ox изобразим на расчетной схеме. Кроме того, запишем выражение для силы инерции груза

,

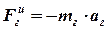(29)

и для момента сил инерции барабана

.

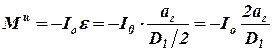(30)

Согласно принципу Даламбера, система двух тел находится в равновесии. Составим уравнение моментов всех сил, в том числе и инерционных, относительно точки О

.

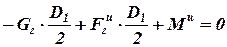(31)

Перепишем его с некоторыми подстановками

.

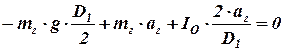Отсюда

.

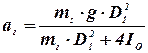(32)

Вычислим угловое ускорение барабана

.

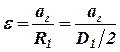(33)

Задача 4. принцип даламбера- лагранжа

Три тела системы соединены нитями. Во всех вариантах движение начинается из состояния покоя в направлении, соответствующем вращению тела 2 против часовой стрелки. Коэффициент трения скольжения f = 0. Плечо трения качения принять также равным нулю. Однако считать, что качение происходит без проскальзывания.

Тело 3 считать однородным цилиндром (для подсчета момента инерции I₃). Исходные числовые данные приведены в таблице 8.

Таблица 7 – Варианты расчетных схем (номер варианта соответствует предпоследней цифре шифра)

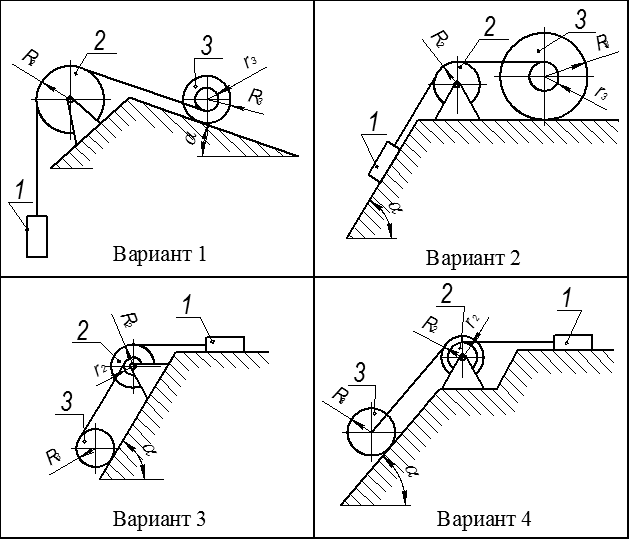
Продолжение таблицы 7

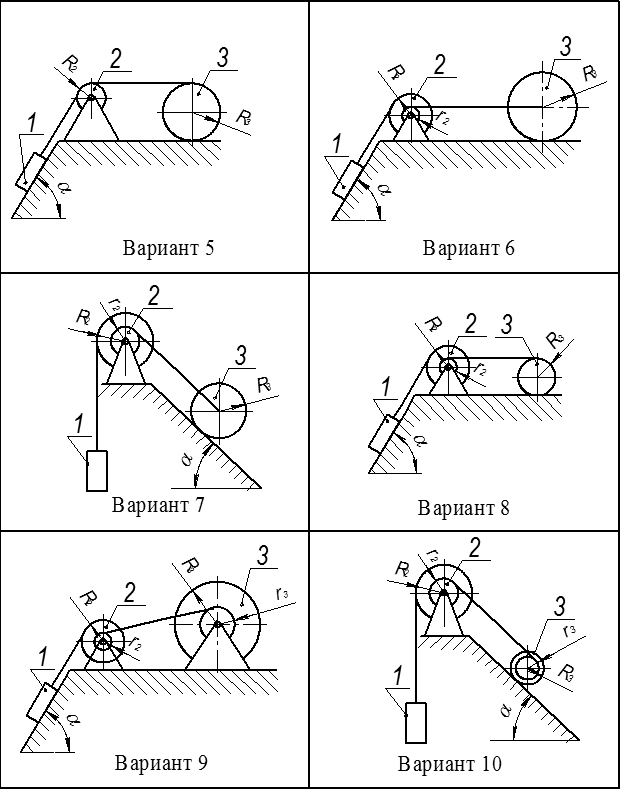
Таблица 8 – Исходные данные для задачи 4

Предпоследняя цифра шифра	Масса тела 1, m1, кг	Момент инерции тела 2, I2, кг ∙ м2	Масса тела 3, m3, кг	Размеры второго тела	Размеры третьего тела	Угол наклона плоскости, a, º (град)
R2, м	r2, м	R3, м	r3, м
		1,5		0,2	0,15	0,25	0,22
		1,8		0,25	0,22	0,3	0,25
		1,4		0,3	0,25	0,25	0,15
		1,3		0,24	0,2	0,3	0,2
		1,2		0,22	0,16	0,26	0,18
		1,4		0,25	0,15	0,2	0,15
		1,3		0,3	0,2	0,22	0,16
		1,1		0,3	0,24	0,24	0,2
		1,4		0,26	0,18	0,2	0,16
		1,1		0,2	0,15	0,28	0,2

Пример 4

Условие задачи. Дана механическая система, состоящая из тел 1, 2, 3, 4 (рисунок 7). Тела 2 и 3 находятся в зацеплении. Масса тел: m₁ = 20 кг, m₄ = 10 кг, моменты инерции тел I₂ = 0,05 кг ∙ м², I₃ = 0,2 кг ∙ м², I₄ = 0,1 кг ∙ м². Углы a = 60°, b = 45°. Коэффициент трения скольжения f = 0,2. Радиусы колес r₂ = 0,1 м, R₂ = 0,2 м, r₃ = 0,15 м, R₃ = 0,3 м, r₄ = 0,2 м. Коэффициент трения качения k = 5 мм = 0,005 м.

Определить: 1 линейное ускорение тела 1, т.е. a₁;

2 угловое ускорение тел 2, 3, 4: e₂, e₃, e₄.

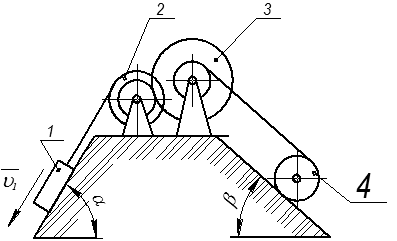
Рисунок 7 – Схема механизма

Решение

Решение задачи выполняем с использованием принципа Даламбера – Лагранжа.

Выделим систему тел 1, 2, 3, 4, соединенных нитью, и изобразим их.

Вместо отброшенных связей изобразим силы реакции. Предварительно изобразим оси x и x¢ вдоль наклонных поверхностей. Положительное направление осей – в сторону движения. Сила нормальной реакции 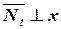. Сила трения F_тр – навстречу движению. Силы реакции R₀₂ и R₀₃ взамен отброшенных шарнирных неподвижных опор прикладываем в точках O₂ и O₃ и направляем их произвольно, т.к. направление их неизвестно. Нормальную реакцию N₄ прикладываем со смещением на величину плеча трения качения k в ту сторону, чтобы сила 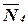препятствовала качению тела 4.

На следующем этапе работы прикладываем силы тяжести 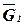, , 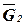, 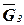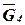в центрах тяжести соответствующих тел, отмечаем углы a и b, которые векторы 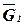и 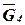образуют с выбранными координатами осями.

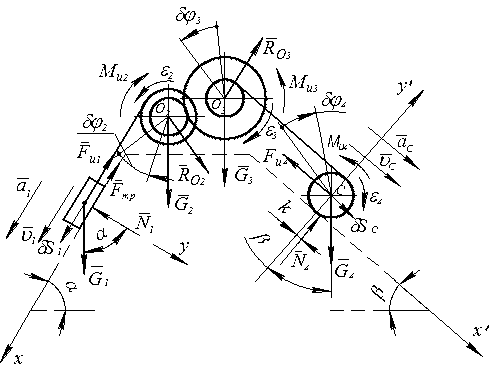
Рисунок 8 – Схема для решения задачи

Чтобы воспользоваться принципом Даламбера, изобразим все инерционные факторы: силы инерции и моменты инерционные. Используя направление a₁, изобразим угловые ускорения e₂, e₃, e₄ и ускорение центра тяжести четвертого тела: a_с. (Вектор 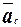изображен в стороне от точки C как и некоторые другие кинематические характеристики из-за «тесноты» на рисунке 8).

Первое тело: сила инерции F_u1= – m₁∙a₁. Направляем силу инерции навстречу a₁. Второе тело. M_u2 = – I₂ ∙ e₂.МоментM_u2 направляем на рисунке навстречу e₂.

Так же поступаем с остальными инерционными нагрузками.

Mu3 = – I3 ∙ e3;	(34)
Mu4 = – I4 ∙ e4;	(35)
Fu4 = – m4 ∙ aс.	(36)

Теперь, согласно принципу Даламбера, после того, как изображены все реальные силы и инерционные силовые факторы (силы и моменты) система сил, изображенная на рисунке 8, условно является уравновешенной. А, значит, для неё можно записывать любые уравнения равновесия.

Разъяснения. Условность состоит в том, что на самом деле система движется, и все тела движутся с ускорениями. Но если вместе с реальными силами изображены (учтены) инерционные силы и моменты, то согласно принципу Даламбера, для такой системы могут быть записаны любые уравнения равновесия.

Однако мы не воспользуемся этим «разрешением», а используем принцип Лагранжа, который состоит в том, что системе, находящейся в равновесии, т.е. неподвижной, дадим малое перемещение (возможное, виртуальное). Все силы и моменты пар сил совершат работу на соответствующих (своих) перемещениях. Сумма этих работ равна нулю, т.к. система находится в равновесии, пусть даже и условном.

Условно неподвижной системе даем малое возможное (виртуальное) перемещение. Тело 1 переместится на величину dS₁, тело 2 – повернется на угол dj₂, тело 3 – на угол dj₃, тело 4, скатываясь, повернется на угол dj₄, а центр C переместится на dS_с. С использованием зависимостей кинематики установим соответствие между всеми возможными перемещениями.

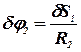;	(37)
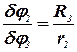;	(38)
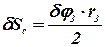;	(39)
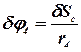.	(40)

Связь между ускорениями тел записывается аналогично. Следующие формулы могут быть получены из предыдущих заменой характеристик перемещения dj, S на ускорения e, а, сохраняя прежние индексы.

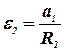;	(41)
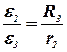;	(42)
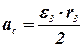;	(43)
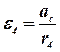.	(44)

Запишем общее уравнение динамики .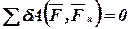

Слагаемые суммы, записанной в левой части этого уравнения, могут быть вычислены по следующим формулам:

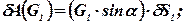	(45)
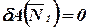;	(46)
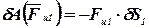;	(47)
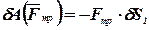;	(48)
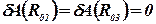;	(49)
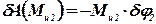;	(50)
dА (G2) = dА (G3) = 0;	(51)
dА (Мu3) = – Mu3 ∙ dj3;	(52)
dА (Мu4) = – Mu4 ∙ dj4;	(53)
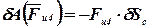;	(54)
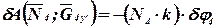;	(55)
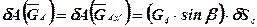.	(56)

Все перемещения 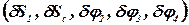выразим через одно, любое из них. Выразим все перемещения через dS₁ с использованием выражений (38).

Решение обычно ведут в общем виде, сохраняя символьное (буквенное) обозначение параметров до получения искомой величины. Это позволяет анализировать полученный результат: определять влияние изменения исходных данных на получаемый результат. Однако в данном примере, чтобы избежать громоздких выражений, будем производить вычисления уже на следующей стадии работы.

.

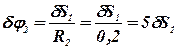
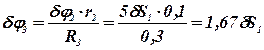
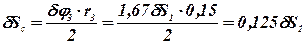
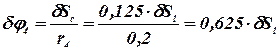Точно так же все ускорения выразим через одно, но не любое, а искомое ускорение a₁, и выполним возможные вычисления.

;

;

;

.

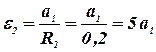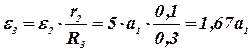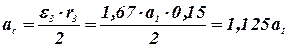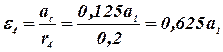Принимаем для упрощения расчетов 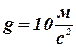и вычисляем элементарную работу

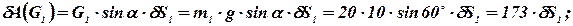
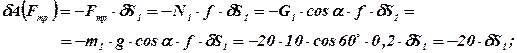
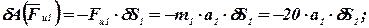
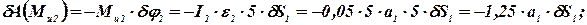
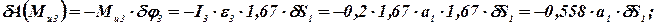
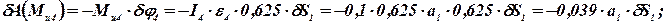
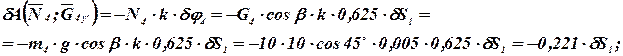
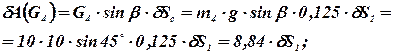
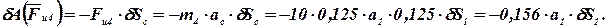
Общее уравнение динамики, записанное ранее в общем виде 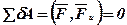, теперь, с учетом выполненных преобразований, можно записать так:

173 ∙ dS₁ – 20 ∙ dS₁ – 20 ∙ a₁ ∙ dS₁ – 1,25 ∙ a₁ ∙ dS₁ –0,558∙ a₁ ∙ dS₁ –

– 0,039 ∙ a₁ ∙ dS₁ – 0,221 ∙ dS₁ + 8,84 ∙ dS₁ – 0,156 ∙ a₁ ∙ dS₁ = 0

Разделим левую и правую части этого выражения на dS₁.

Полученное выражение преобразуем, сгруппировав в левой части слагаемые, содержащие a₁:

20 a₁ + 1,25 ∙ a₁ + 0,558 ∙ a₁ + 0,039 ∙ a₁ +0,156∙a₁ = 173 – 20 – 0,221 + 8,84

Отсюда

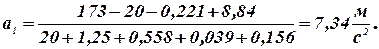
СПИСОК ЛИТЕРАТУРЫ

1. Лачуга Ю.Ф., Ксендзов В.А. Теоретическая механика / Ю.Ф.Лачуга, В.А. Ксендзов– 2-е изд., перераб. и доп., ил. – М.: изд-во «Лань», 2005. – 35 с.

2. Сборник задач для курсовых работ по теоретической механике / под ред. А.А.Яблонского. – М.: Высшая школа, 1985. – 367 с.

3. Лапшин П.Н., Манило И.И. Стандарт предприятия. Учебно-методическая документация. Общие требования к оформлению. СТП КГСХА 01-2006. / П.Н. Лапшин, И.И. Манило. – Курган.: изд-во КГСХА, 2006. – 35с.

Родионов С.С., Родионова С.И., Корнеев Л.А., Королев А.Е.Теоретическая механика. Методические указания и контрольные задания по разделу «Динамика».– Курган.: Изд-во КГСХА, 2011. - 33 с.

Авторы:

Сергей Сергеевич Родионов

София Игоревна Родионова

Леонид Андреевич Корнеев

Александр Евгеньевич Королев