Анализ неустановившегося движения машинного агрегата.

Неустановившейся режим имеет место, когда агрегат пускают в ход и он, набирая скорость, выходит на установившейся режим, а также когда для остановки машины её двигатель отключают и она продолжает двигаться за счёт накопленного запаса кинетической энергии; при этом машина постепенно теряет скорость из-за действия сил трения или каких-либо сил сопротивления, в том числе и специальных тормозных сил (рис.17.1).

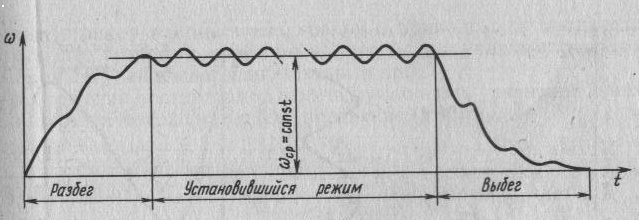
Рис.17.1

В этих случаях нужно знать, насколько быстро происходит переход из неподвижного состояния в рабочее и обратный процесс до полной остановки.

Применительно к транспортным и грузоподъёмным машинам это важно для определения времени разбега и выбега (торможения) , расчёта длины тормозного пути.

Разбег и торможение могут происходить с большим ускорением. Это вызывает значительное динамическое нагружение механизма, что, в свою очередь, может привести к перенапряжениям и даже к поломкам.

Во время разбега и выбега угловая скорость многих машин может проходить через критическую (резонансную) зону. Во избежание динамической перегрузки механизма и возможной аварии проход этой зоны должен быть достаточно быстрым, что надо обеспечить при проектировании, сделав расчёт обеих фаз неустановившегося режима.

При анализе неустановившегося режима следует использовать уравнение движения машинного агрегата в дифференциальной форме (15.9).

Оно выглядит следующим образом:

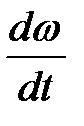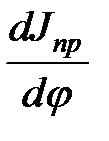
J_пр + 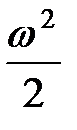= М_пр. (17.1)

Здесь: J_пр – приведённый к ведущему звену момент инерции всех подвижных звеньев механизма;

М_пр- приведённый момент всех учитываемых сил, действующих в агрегате.

Для определения закона движения при неустановившемся режиме должны быть известны следующие данные: кинематическая схема и размеры механизма; массы и моменты инерции звеньев; механические характеристики сил и моментов; начальные условия движения.

Рассмотрим случай работы агрегата при следующих условиях:

а) Приведённый к ведущему звену момент инерции всех подвижных звеньев механизма J_пр=const.;

б) Механическая характеристика момента движущих сил- линейна (рис.17.2) и представляется (рис.17.2) в виде:

М_Д= М₀- b*ω , (17.2)

где : М₀ – пусковой момент двигателя;

b – коэффициент, характеризующий крутизну спада характеристики;

М_Н – номинальный развиваемый момент движущих сил, соответствующий номинальной угловой скорости ω_Н;

в) Приведённый момент сил сопротивления М_С= const. (рис.17.2)

(силы трения не учитываются);

г) Предполагается, что двигатель подобран таким образом, что М_С=М_Н,

а ω_Н соответствует угловой скорости ω_уст установившегося режима работы агрегата.

М

М₀ М_Д

М_С

М_Н А

0 ω_Н = ω_УСТ. ω

Рис.17.2

Типичным примером для таких условий является работа при пуске и торможении многих грузоподъёмных устройств с приводом от шунтового двигателя постоянного тока.

В соответствии с заданными условиями уравнение (17.1) запишется в виде:

J_пр 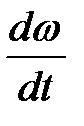= М₀- b*ω -М_С. (17.3)

Из равенства в точке А моментов М_Д и М_С

коэффициент b=(М₀-М_С)/ω_Н (17.4)

Подставляя выражение (17.4) в уравнение движения (17.3) после преобразований получаем:

dt=(J_пр/(m₀-m_C)*( dω/(1-ω/ω_Н)) (17.5)

Используем табличный интеграл : ∫ 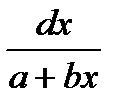=(1/b)* ln (a+bx) и

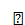
интегрируем уравнение (17.5):

t=-T * ln(1- ω/ ω_уст) + C, (17.6)

где Т= J_пр * ω_уст /(m₀-m_C) (17.6)

С- постоянная интегрирования.

При t=0, ω=0 . Следовательно С=0.

Преобразовывая уравнение (17.6), получаем уравнение движения агрегата при разгоне:

ω= ω_уст(1-е^-t/T) (17.7)

График изменения угловой скорости при разгоне представлен на рис.17.3.

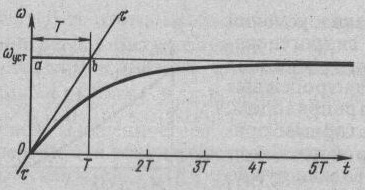
Рис.17.3

Величина Т , определяемая по формуле (17.6), называется постоянной времени машинного агрегата. Графически на рис.17.3 она представляет собой отрезок ab. Физический смысл её в следующем. Если бы в процессе разгона разница (М_Д-М_С) не уменьшалась, а оставалась бы равной М₀ (как в начальный момент), то движение было бы равноускоренным, а угловая скорость достигала бы значения ω_уст через время Т.

Теоретически разгон продолжается бесконечно долго. Однако уже при t=3Т отношение ω/ ω_уст составит 0,95, при t=4Т оно возрастёт до 0,98, а при t=5Т до 0,995, то есть процесс разгона при t=(4-5)Т практически завершается. Отсюда следует, что если задать время разгона, то можно определить соответствующую величину J_пр, при которой процесс разгона действительно займёт заданное время.

Расчёт времени торможения (выбега) машинного агрегата.

Принимаем , как и при разгоне , J_пр=const.

В начальный момент торможения выключается двигатель и включается тормоз. Следовательно М_Д=0, а М_С=М_ТОРМ.

Уравнение движения (17.1) при этом приобретает после преобразований следующий вид:

dt=-(J_пр/m_ТОРМ)* dω (17.8)

Интегрируем данное уравнение:

t =-(J_пр/m_ТОРМ)* ω +С₁ (17.9)

Постоянная интегрирования С₁ находится из начальных условий:

При t=0 ω=ω_уст. Следовательно С₁==(J_пр/m_ТОРМ)* ω_УСТ.

Подставляя в уравнение (17.9), получаем линейное уравнение для определения времени торможения агрегата при заданных условиях.

t =(J_пр/m_ТОРМ)* ( ω _УСТ - ω) . (17.10)

При полной остановке (ω=0) находится время торможения:

t =(J_пр/m_ТОРМ)* ω_УСТ . (17.11)

Характер графика торможения представлен на рис.17.4.

ω

ω_уст

t

t_ТОРМ

Рис.17.4

Рекомендуемая литература.

1. Фролов К.В. Теория механизмов и машин. - М.: Высш. шк., 2005..

2. Иосилевич Г.Б. Прикладная механика. - М.: Высш.шк., 1989.

3. Трубняков В.А. Кинематический и силовой расчёт механизмов: Метод.

указания к выполнению курсового проекта. - СПб.: ПИМаш,2005.

4. Либуркин Л.Я. Динамика машин с учётом характеристики двигателя: