Молекулярная физика и термодинамика 2 страница
5000 |  |
Решение:
Согласно первому началу термодинамики, 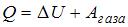 , где
, где 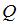 – количество теплоты, полученное газом,
– количество теплоты, полученное газом, 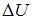 – приращение его внутренней энергии,
– приращение его внутренней энергии, 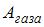 – работа, совершенная газом. Отсюда
– работа, совершенная газом. Отсюда 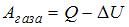 . Приращение внутренней энергии в данном случае
. Приращение внутренней энергии в данном случае 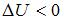 , так как температура газа в ходе процесса понизилась.
, так как температура газа в ходе процесса понизилась. 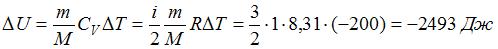 . Тогда работа, совершенная газом, равна
. Тогда работа, совершенная газом, равна 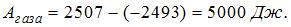
 ЗАДАНИЕ N 2 сообщить об ошибке
ЗАДАНИЕ N 2 сообщить об ошибке
Тема: Второе начало термодинамики. Энтропия
Если КПД цикла Карно равен 60%, то температура нагревателя больше температуры холодильника в ______ раз(а).
 |  | 2,5 | |
 | |||
 | |||
 | 1,7 |
Решение:
КПД обратимого цикла Карно равен: 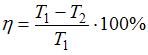 , или
, или 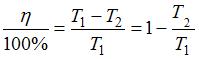 ; следовательно,
; следовательно, 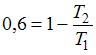 ; отсюда
; отсюда 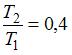 и
и 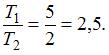
 ЗАДАНИЕ N 3 сообщить об ошибке
ЗАДАНИЕ N 3 сообщить об ошибке
Тема: Распределения Максвелла и Больцмана
На рисунке представлен график функции распределения молекул идеального газа по скоростям (распределение Максвелла), где 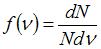 – доля молекул, скорости которых заключены в интервале скоростей от
– доля молекул, скорости которых заключены в интервале скоростей от 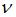 до
до 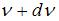 в расчете на единицу этого интервала:
в расчете на единицу этого интервала:
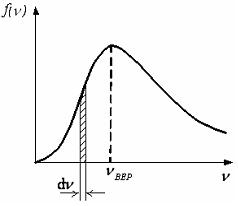
Для этой функции верными являются утверждения …
 |  | положение максимума кривой зависит не только от температуры, но и от природы газа (его молярной массы) | |
 |  | при увеличении числа молекул площадь под кривой не изменяется | |
 | с ростом температуры газа значение максимума функции увеличивается | ||
 | для газа с бόльшей молярной массой (при той же температуре) максимум функции расположен в области бόльших скоростей |
Решение:
Из определения функции распределения Максвелла следует, что выражение 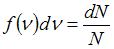 определяет долю молекул, скорости которых заключены в интервале скоростей от
определяет долю молекул, скорости которых заключены в интервале скоростей от 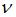 до
до 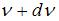 (на графике это – площадь заштрихованной полоски). Тогда площадь под кривой равна
(на графике это – площадь заштрихованной полоски). Тогда площадь под кривой равна 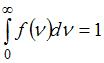 и не изменяется при изменении температуры и числа молекул газа. Из формулы наиболее вероятной скорости
и не изменяется при изменении температуры и числа молекул газа. Из формулы наиболее вероятной скорости 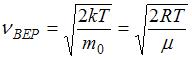 (при которой функция
(при которой функция 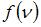 максимальна) следует, что
максимальна) следует, что 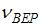 прямо пропорциональна
прямо пропорциональна 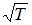 и обратно пропорциональна
и обратно пропорциональна 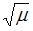 , где
, где 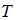 и
и 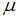 – температура и молярная масса газа соответственно.
– температура и молярная масса газа соответственно.
 ЗАДАНИЕ N 4 сообщить об ошибке
ЗАДАНИЕ N 4 сообщить об ошибке
Тема: Средняя энергия молекул
Если не учитывать колебательные движения в молекуле углекислого газа, то средняя кинетическая энергия молекулы равна …
 |  | 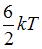 | |
 | 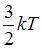 | ||
 | 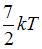 | ||
 | 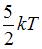 |
Решение:
Средняя кинетическая энергия молекулы равна: 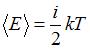 , где
, где 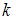 – постоянная Больцмана,
– постоянная Больцмана, 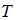 – термодинамическая температура;
– термодинамическая температура; 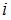 – сумма числа поступательных, вращательных и удвоенного числа колебательных степеней свободы молекулы:
– сумма числа поступательных, вращательных и удвоенного числа колебательных степеней свободы молекулы: 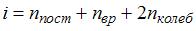 . Для молекулы углекислого газа
. Для молекулы углекислого газа  число степеней свободы поступательного движения
число степеней свободы поступательного движения 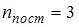 , вращательного –
, вращательного – 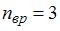 , колебательного –
, колебательного – 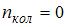 , поэтому
, поэтому 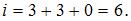
Следовательно, средняя кинетическая энергия молекулы 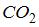 равна:
равна: 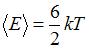 .
.
ЗАДАНИЕ N 25 сообщить об ошибке
Тема: Первое начало термодинамики. Работа при изопроцессах
Двум молям водорода сообщили 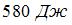 теплоты при постоянном давлении. При этом его температура повысилась на ______ К.
теплоты при постоянном давлении. При этом его температура повысилась на ______ К.
(Считать связь атомов в молекуле жесткой. 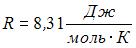 )
)
Ответ округлите до целого числа.
10 |  |
Решение:
Согласно первому началу термодинамики, количество теплоты, получаемое газом, равно 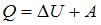 , где
, где 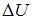 – изменение внутренней энергии,
– изменение внутренней энергии, 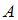 – работа газа. Количество теплоты, сообщаемое газу при постоянном давлении можно представить в виде
– работа газа. Количество теплоты, сообщаемое газу при постоянном давлении можно представить в виде 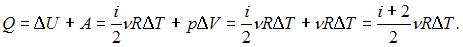 Здесь
Здесь 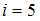 – число степеней свободы молекул двухатомного газа с жесткой связью атомов в молекуле. Отсюда
– число степеней свободы молекул двухатомного газа с жесткой связью атомов в молекуле. Отсюда 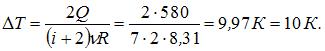
 ЗАДАНИЕ N 26 сообщить об ошибке
ЗАДАНИЕ N 26 сообщить об ошибке
Тема: Второе начало термодинамики. Энтропия
Максимальное значение КПД, которое может иметь тепловой двигатель с температурой нагревателя 327°С и температурой холодильника 27°С, составляет ____ %.
 |  | ||
 | |||
 | |||
 |
Решение:
КПД реального теплового двигателя всегда меньше КПД идеального (обратимого) теплового двигателя, работающего в тех же условиях, то есть при одних и тех же температурах нагревателя и холодильника. Коэффициент полезного действия идеального теплового двигателя определяется только температурами нагревателя и холодильника: 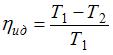 . Таким образом, максимальное значение КПД, которое может иметь рассматриваемый тепловой двигатель, равно
. Таким образом, максимальное значение КПД, которое может иметь рассматриваемый тепловой двигатель, равно 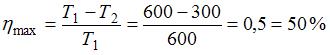 .
.
 ЗАДАНИЕ N 27 сообщить об ошибке
ЗАДАНИЕ N 27 сообщить об ошибке
Тема: Распределения Максвелла и Больцмана
На рисунке представлен график функции распределения молекул идеального газа по скоростям (распределение Максвелла), где 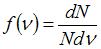 – доля молекул, скорости которых заключены в интервале скоростей от
– доля молекул, скорости которых заключены в интервале скоростей от 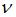 до
до 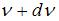 в расчете на единицу этого интервала:
в расчете на единицу этого интервала:

Для этой функции верными являются утверждения …
 |  | положение максимума кривой зависит не только от температуры, но и от природы газа (его молярной массы) | |
 |  | при увеличении числа молекул площадь под кривой не изменяется | |
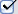 | с ростом температуры газа значение максимума функции увеличивается | ||
 | для газа с бόльшей молярной массой (при той же температуре) максимум функции расположен в области бόльших скоростей |
Решение:
Из определения функции распределения Максвелла следует, что выражение 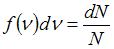 определяет долю молекул, скорости которых заключены в интервале скоростей от
определяет долю молекул, скорости которых заключены в интервале скоростей от 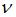 до
до 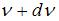 (на графике это – площадь заштрихованной полоски). Тогда площадь под кривой равна
(на графике это – площадь заштрихованной полоски). Тогда площадь под кривой равна 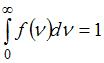 и не изменяется при изменении температуры и числа молекул газа. Из формулы наиболее вероятной скорости
и не изменяется при изменении температуры и числа молекул газа. Из формулы наиболее вероятной скорости 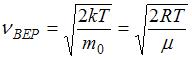 (при которой функция
(при которой функция 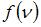 максимальна) следует, что
максимальна) следует, что 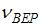 прямо пропорциональна
прямо пропорциональна 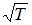 и обратно пропорциональна
и обратно пропорциональна 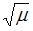 , где
, где 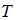 и
и 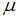 – температура и молярная масса газа соответственно.
– температура и молярная масса газа соответственно.
 ЗАДАНИЕ N 28 сообщить об ошибке
ЗАДАНИЕ N 28 сообщить об ошибке
Тема: Средняя энергия молекул
Если не учитывать колебательные движения в молекуле водорода при температуре 200 К, то кинетическая энергия в (Дж)всех молекул в 4 г водорода равна …
 |  | 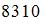 | |
 | 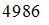 | ||
 | 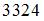 | ||
 | 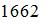 |
Решение:
Средняя кинетическая энергия одной молекулы равна: 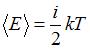 , где
, где 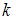 – постоянная Больцмана,
– постоянная Больцмана, 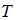 – термодинамическая температура;
– термодинамическая температура; 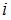 – сумма числа поступательных, числа вращательных и удвоенного числа колебательных степеней свободы молекулы
– сумма числа поступательных, числа вращательных и удвоенного числа колебательных степеней свободы молекулы 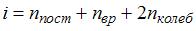 . Молекула водорода
. Молекула водорода 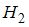 имеет 3 поступательные и 2 вращательные степени свободы, следовательно,
имеет 3 поступательные и 2 вращательные степени свободы, следовательно, 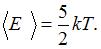 В 4 г водорода содержится
В 4 г водорода содержится 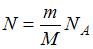 молекул, где
молекул, где 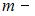 масса газа,
масса газа, 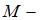 молярная масса водорода,
молярная масса водорода, 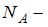 число Авогадро. Кинетическая энергия всех молекул будет равна:
число Авогадро. Кинетическая энергия всех молекул будет равна: 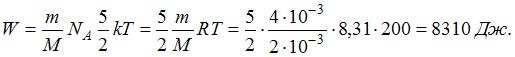
ЗАДАНИЕ N 17 сообщить об ошибке
Тема: Второе начало термодинамики. Энтропия
В ходе необратимого процесса при поступлении в неизолированную термодинамическую систему тепла для приращения энтропии верным будет соотношение …
 |  | 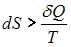 | |
 | 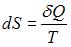 | ||
 | 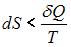 | ||
 | 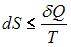 |
Решение:
Отношение 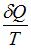 в обратимом процессе есть полный дифференциал функции состояния системы, называемой энтропией
в обратимом процессе есть полный дифференциал функции состояния системы, называемой энтропией 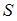 системы:
системы: 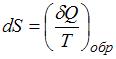 . В изолированных системах энтропия не может убывать при любых, происходящих в ней процессах:
. В изолированных системах энтропия не может убывать при любых, происходящих в ней процессах: 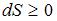 . Знак равенства относится к обратимым процессам, а знак «больше» – к необратимым процессам. Если в неизолированную систему поступает тепло и происходит необратимый процесс, то энтропия возрастает за счет не только полученного тепла, но и необратимости процесса:
. Знак равенства относится к обратимым процессам, а знак «больше» – к необратимым процессам. Если в неизолированную систему поступает тепло и происходит необратимый процесс, то энтропия возрастает за счет не только полученного тепла, но и необратимости процесса: 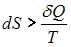 .
.
 ЗАДАНИЕ N 18 сообщить об ошибке
ЗАДАНИЕ N 18 сообщить об ошибке
Тема: Первое начало термодинамики. Работа при изопроцессах
Один моль идеального одноатомного газа в ходе некоторого процесса получил 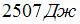 теплоты. При этом его температура понизилась на
теплоты. При этом его температура понизилась на 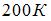 . Работа (
. Работа ( 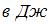 ), совершенная газом, равна …
), совершенная газом, равна … 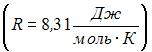
5000 | 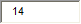 |
Решение:
Согласно первому началу термодинамики, 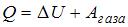 , где
, где 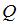 – количество теплоты, полученное газом,
– количество теплоты, полученное газом, 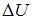 – приращение его внутренней энергии,
– приращение его внутренней энергии, 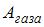 – работа, совершенная газом. Отсюда
– работа, совершенная газом. Отсюда 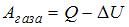 . Приращение внутренней энергии в данном случае
. Приращение внутренней энергии в данном случае 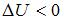 , так как температура газа в ходе процесса понизилась.
, так как температура газа в ходе процесса понизилась. 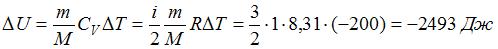 . Тогда работа, совершенная газом, равна
. Тогда работа, совершенная газом, равна 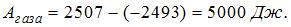
 ЗАДАНИЕ N 19 сообщить об ошибке
ЗАДАНИЕ N 19 сообщить об ошибке
Тема: Средняя энергия молекул
Отношение средней кинетической энергии вращательного движения к средней энергии молекулы с жесткой связью 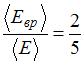 . Это имеет место для …
. Это имеет место для …
 |  | водорода | |
 | водяного пара | ||
 | гелия | ||
 | метана ( 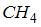 ) ) |
Решение:
Средняя кинетическая энергия молекулы равна: 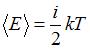 , где
, где 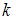 – постоянная Больцмана,
– постоянная Больцмана, 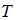 – термодинамическая температура,
– термодинамическая температура, 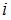 – сумма числа поступательных, вращательных и удвоенного числа колебательных степеней свободы молекулы:
– сумма числа поступательных, вращательных и удвоенного числа колебательных степеней свободы молекулы: 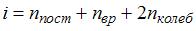 . Средняя энергия вращательного движения
. Средняя энергия вращательного движения 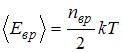 . Таким образом, с учетом того что связь атомов в молекуле по условию является жесткой (в этом случае
. Таким образом, с учетом того что связь атомов в молекуле по условию является жесткой (в этом случае 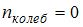 ), отношение
), отношение 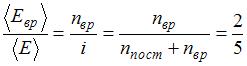 . Отсюда
. Отсюда 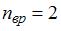 , что имеет место для газов с двухатомными и многоатомными линейными молекулами. Следовательно, это – водород.
, что имеет место для газов с двухатомными и многоатомными линейными молекулами. Следовательно, это – водород.
 ЗАДАНИЕ N 20 сообщить об ошибке
ЗАДАНИЕ N 20 сообщить об ошибке
Тема: Распределения Максвелла и Больцмана
На рисунке представлены графики функций распределения молекул идеального газа 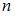 во внешнем однородном поле силы тяжести от высоты
во внешнем однородном поле силы тяжести от высоты 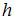 для двух разных газов, где
для двух разных газов, где 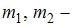 массы молекул газа (распределение Больцмана).
массы молекул газа (распределение Больцмана).
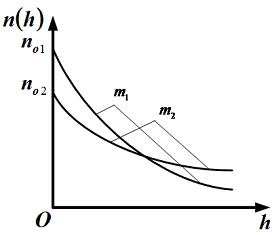
Для этих функций верными являются утверждения, что …
 |  | масса 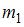 больше массы больше массы 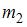 | |
 |  | концентрация молекул газа с меньшей массой на «нулевом уровне» 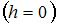 меньше меньше | |
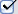 | масса 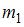 меньше массы меньше массы 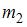 | ||
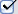 | концентрация молекул газа с меньшей массой на «нулевом уровне» 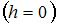 больше больше |
Решение:
Зависимость концентрации молекул идеального газа от высоты 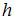 для некоторой температуры
для некоторой температуры 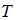 определяется распределением Больцмана:
определяется распределением Больцмана: 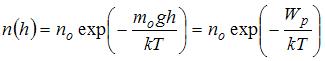 , где
, где 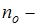 концентрация молекул на высоте
концентрация молекул на высоте 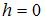 ,
, 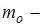 масса молекулы,
масса молекулы, 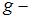 ускорение свободного падения,
ускорение свободного падения, 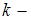 постоянная Больцмана. Из формулы следует, что при постоянной температуре концентрация газа больше там, где меньше потенциальная энергия его молекул
постоянная Больцмана. Из формулы следует, что при постоянной температуре концентрация газа больше там, где меньше потенциальная энергия его молекул 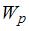 , и уменьшается с высотой по экспоненциальному закону. При одной и той же температуре молекулы, имеющие меньшую массу, более равномерно распределяются по высоте, и поэтому концентрация молекул газа на «нулевом уровне»
, и уменьшается с высотой по экспоненциальному закону. При одной и той же температуре молекулы, имеющие меньшую массу, более равномерно распределяются по высоте, и поэтому концентрация молекул газа на «нулевом уровне» 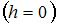 уменьшается, а на высоте
уменьшается, а на высоте 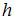 увеличивается.
увеличивается.
