Линейные преобразования графиков функций
В этом параграфе мы рассмотрим основные линейные преобразования графиков функций – параллельный перенос графика функции и растяжение графика функции.
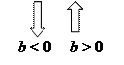 1. Параллельный перенос графика функции
1. Параллельный перенос графика функции 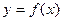 вдоль оси OY, то есть построение графика вида
вдоль оси OY, то есть построение графика вида 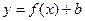 . Если
. Если 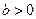 , то ординаты всех точек графика функции увеличиваются на b единиц, а если
, то ординаты всех точек графика функции увеличиваются на b единиц, а если 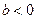 , то ординаты всех точек графика функции уменьшаются на
, то ординаты всех точек графика функции уменьшаются на 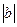 единиц.
единиц.
 2. Параллельный перенос графика функции
2. Параллельный перенос графика функции 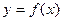 вдоль оси OХ, то есть построение графика вида
вдоль оси OХ, то есть построение графика вида 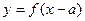 . Если
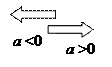
. Если 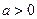 , то график функции сдвигается на а единиц вправо, а если
, то график функции сдвигается на а единиц вправо, а если 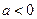 , то график функции сдвигается на
, то график функции сдвигается на 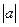 единиц влево.
единиц влево.
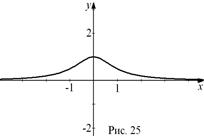
Пример 5. Задан график функции 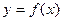 (рис. 25). Постройте графики функций
(рис. 25). Постройте графики функций 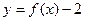 и
и 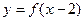 .
.
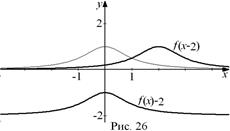
Решение. Перенесем заданный график функции на две единицы вниз или вправо соответственно (рис. 26).
3. Построение графика функции 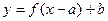 осуществляется последовательным выполнением параллельных переносов графика функции
осуществляется последовательным выполнением параллельных переносов графика функции 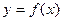 вдоль осей координат.
вдоль осей координат.
Пример 6. Постройте график функции 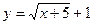 .
.
 Решение. Известный график степенной функции
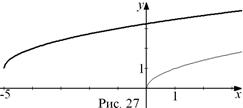
Решение. Известный график степенной функции 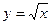 (рис. 9) перенесем на единицу вверх и на пять единиц влево (рис. 27).
(рис. 9) перенесем на единицу вверх и на пять единиц влево (рис. 27).
4. «Растяжение» графика функции 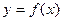 от оси OХ, то есть построение графика функции
от оси OХ, то есть построение графика функции 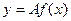 . Если
. Если 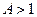 , то ордината каждой точки графика увеличивается в А раз (растяжение графика функции от оси OХ) и уменьшается в
, то ордината каждой точки графика увеличивается в А раз (растяжение графика функции от оси OХ) и уменьшается в 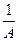 раз, если
раз, если 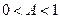 (сжатие графика функции к оси OХ).
(сжатие графика функции к оси OХ).
 5. Симметрия относительно оси ОХ, то есть построение графика функции
5. Симметрия относительно оси ОХ, то есть построение графика функции 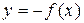 . При этом каждая точка графика функции отображается в точку, симметричную относительно оси OХ.
. При этом каждая точка графика функции отображается в точку, симметричную относительно оси OХ.
6. Построение графика функции 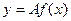 , если
, если  , проводится как последовательное выполнение двух преобразований – симметрии относительно оси OХ и растяжения от оси OХ.
, проводится как последовательное выполнение двух преобразований – симметрии относительно оси OХ и растяжения от оси OХ.
 Пример 7. Задан график функции
Пример 7. Задан график функции 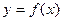 (рис. 25). Постройте графики функций
(рис. 25). Постройте графики функций 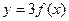 и
и 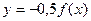 .
.
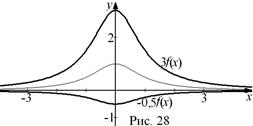
 Решение. График функции
Решение. График функции 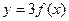 получим растяжением в три раза графика функции
получим растяжением в три раза графика функции 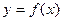 от оси OX. Чтобы построить график функции
от оси OX. Чтобы построить график функции 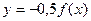 необходимо исходный график сначала отразить относительно оси OХ, а затем сжать его в два раза вдоль оси OY (рис. 28).
необходимо исходный график сначала отразить относительно оси OХ, а затем сжать его в два раза вдоль оси OY (рис. 28).
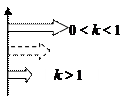
7. «Сжатие» графика функции 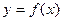 к оси OY, то есть построение графика функции
к оси OY, то есть построение графика функции 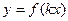 . При
. При 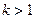 абсциссы точек графика функции уменьшаются в k раз, происходит сжатие графика функции к оси OY. При
абсциссы точек графика функции уменьшаются в k раз, происходит сжатие графика функции к оси OY. При 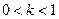 абсциссы точек графика функции увеличиваются в
абсциссы точек графика функции увеличиваются в 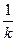 раз, происходит растяжение графика функции от оси OY.
раз, происходит растяжение графика функции от оси OY.
 8. Симметрия относительно оси ОY, то есть построение графика функции
8. Симметрия относительно оси ОY, то есть построение графика функции 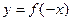 . При этом каждая точка графика функции отображается в точку, симметричную ей относительно оси OY.
. При этом каждая точка графика функции отображается в точку, симметричную ей относительно оси OY.
9. Построение графика функции 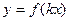 , если
, если 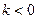 , проводится как последовательное выполнение двух преобразований – симметрии относительно оси OY и сжатия к оси OY.
, проводится как последовательное выполнение двух преобразований – симметрии относительно оси OY и сжатия к оси OY.
Пример 8. Задан график функции 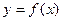 (рис. 25). Постройте графики функций
(рис. 25). Постройте графики функций 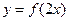 и
и 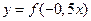 .
.
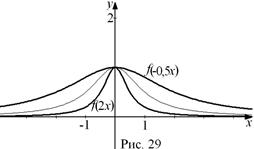 Решение. График функции
Решение. График функции 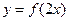 строится путем сжатия графика функции
строится путем сжатия графика функции 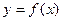 в два раза к оси OY. Для построения графика функции
в два раза к оси OY. Для построения графика функции 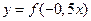 нужно симметрично отразить график исходной функции относительно оси OY и растянуть его вдоль оси OX в два раза (рис. 29). Заметим, что, так как график функции
нужно симметрично отразить график исходной функции относительно оси OY и растянуть его вдоль оси OX в два раза (рис. 29). Заметим, что, так как график функции 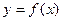 симметричен относительно оси OY, то есть функция
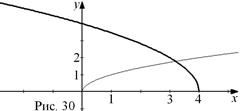
симметричен относительно оси OY, то есть функция 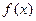 является четной, то отражение относительно OY не меняет вид графика.
является четной, то отражение относительно OY не меняет вид графика.
 Пример 9.Постройте график функции
Пример 9.Постройте график функции 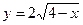 .
.
Решение. Запишем функцию в виде 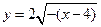 . Следовательно, построение графика производится последовательным выполнением преобразований известного графика функции
. Следовательно, построение графика производится последовательным выполнением преобразований известного графика функции 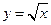 (рис. 9): симметричное отражение относительно оси OY, параллельный перенос на четыре единицы вправо и растяжение графика от оси OХ в два раза (рис. 30).
(рис. 9): симметричное отражение относительно оси OY, параллельный перенос на четыре единицы вправо и растяжение графика от оси OХ в два раза (рис. 30).
