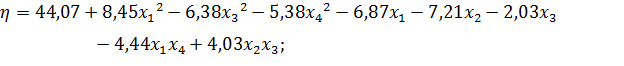Выполнение критериальных проверок
Проверим значимость коэффициентов полученной квазилинейной модели с целью исключения из модели факторов, слабо влияющих на функцию отклика. Коэффициент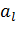 
считается значимым, если он значимо отличается от нуля в смысле критерия Стьюдента.
При количестве опытов в плане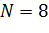 
и количестве повторных опытов 
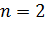число степеней свободы равно 
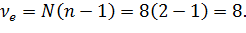Выбираем доверительную вероятность 
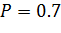и определяем по таблице из приложения 1 значение 
.
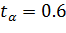Дисперсия наблюдения
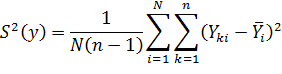
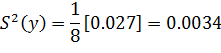
Доверительный интервал коэффициентов аl модели
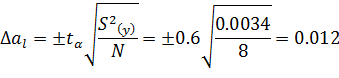
Так как все коэффициенты квазилинейной модели больше доверительного интервала, все они являются значимыми.
Задание №3 Планирование эксперимента. Построение нелинейных уравнений регрессии/
Вариант 60/5.
Особенности плана: композиционный, симметричный, трехуровневый.
«Ядро» плана представляет собой полный факторный эксперимент 2М, а «звездное плечо» выбрано из условия минимализации определителя ковариационной матрицы.
Количество опытов в плане N=24, количество повторных опытов в каждой точке плана n=3, количество факторов M=4.
Характеристики плана: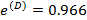 
D –эффективность; 
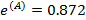A –эффективность; 
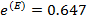E –эффективность; 
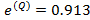Q –эффективность;
Ковариационная матрица имеет вид:
| Номер опыта | x1 | x2 | x3 | x4 | y1 | y2 | y3 |
| -1 | -1 | -1 | -1 | ||||
| -1 | -1 | -1 | |||||
| -1 | -1 | -1 | |||||
| -1 | -1 | ||||||
| -1 | -1 | -1 | |||||
| -1 | -1 | ||||||
| -1 | -1 | ||||||
| -1 | |||||||
| -1 | -1 | -1 | |||||
| -1 | -1 | ||||||
| -1 | -1 | ||||||
| -1 | |||||||
| -1 | -1 | ||||||
| -1 | |||||||
| -1 | |||||||
| -1 | |||||||
| -1 | |||||||
| -1 | |||||||
| -1 |
Решение
Построение модели
Квазилинейная модель имеет вид:
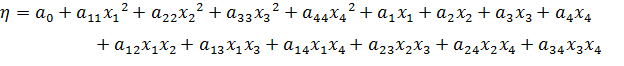
Из ковариационной матрицы С определяем
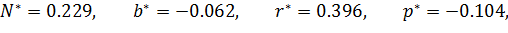
Коэффициенты модели вычислим по следующим формулам:
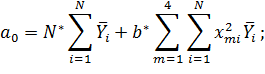
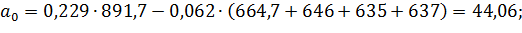
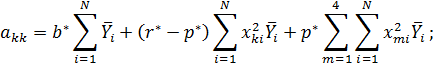
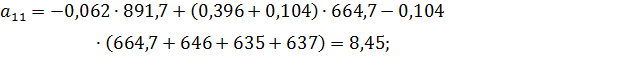
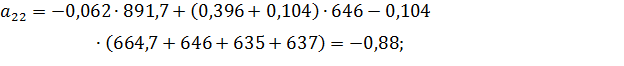
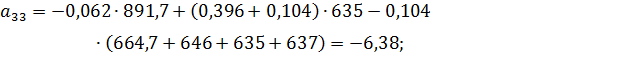
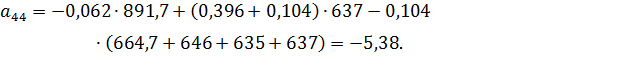
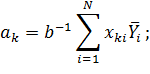
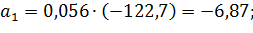
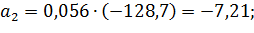
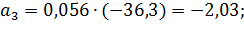
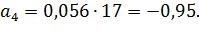
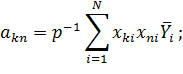
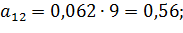
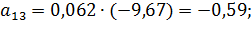
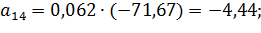
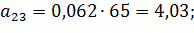
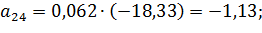
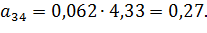
Получили модель:
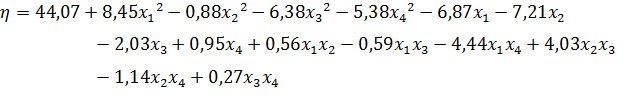
Таблица 4 – Данные для расчёта коэффициентов
| № |  |  |  |  |  |  |  |  |  |  |  |  |
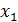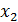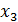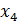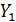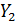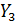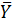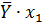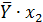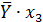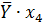| -1 | -1 | -1 | -1 | 51,33333 | -51,3333 | -51,3333 | -51,3333 | -51,3333 | ||||
| -1 | -1 | -1 | 56,66667 | -56,6667 | -56,6667 | -56,6667 | 56,66667 | |||||
| -1 | -1 | -1 | -32 | -32 | -32 | |||||||
| -1 | -1 | -58 | -58 | |||||||||
| -1 | -1 | -1 | 19,66667 | -19,6667 | 19,66667 | -19,6667 | -19,6667 | |||||
| -1 | -1 | -49 | -49 | |||||||||
| -1 | -1 | 38,66667 | -38,6667 | 38,66667 | 38,66667 | -38,6667 | ||||||
| -1 | -27 | |||||||||||
| -1 | -1 | -1 | -54 | -54 | -54 | |||||||
| -1 | -1 | 37,66667 | 37,66667 | -37,6667 | -37,6667 | 37,66667 | ||||||
| -1 | -1 | -22 | -22 | |||||||||
| -1 | 29,33333 | 29,33333 | -29,3333 | 29,33333 | 29,33333 | |||||||
| -1 | -1 | 23,33333 | 23,33333 | 23,33333 | -23,3333 | -23,3333 | ||||||
| -1 | -16 | |||||||||||
| -1 | 27,66667 | 27,66667 | 27,66667 | 27,66667 | -27,6667 | |||||||
| 21,33333 | 21,33333 | 21,33333 | 21,33333 | 21,33333 | ||||||||
| 39,66667 | 39,66667 | |||||||||||
| -1 | 61,33333 | -61,3333 | ||||||||||
| -1 | 46,33333 | -46,3333 | ||||||||||
| 43,33333 | 43,33333 | |||||||||||
| -1 | -28 | |||||||||||
| -1 | 41,33333 | -41,3333 | ||||||||||
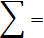 | 891,666 | -122,667 | -128,667 | -36,3333 |
Таблица 5 – Данные для расчёта коэффициентов
| № | | | | | | | | |  |  |  |  |
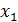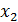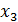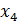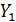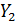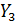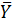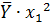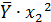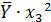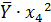| -1 | -1 | -1 | -1 | 51,33333 | 51,33333 | 51,33333 | 51,33333 | 51,33333 | ||||
| -1 | -1 | -1 | 56,66667 | 56,66667 | 56,66667 | 56,66667 | 56,66667 | |||||
| -1 | -1 | -1 | ||||||||||
| -1 | -1 | |||||||||||
| -1 | -1 | -1 | 19,66667 | 19,66667 | 19,66667 | 19,66667 | 19,66667 | |||||
| -1 | -1 | |||||||||||
| -1 | -1 | 38,66667 | 38,66667 | 38,66667 | 38,66667 | 38,66667 | ||||||
| -1 | ||||||||||||
| -1 | -1 | -1 | ||||||||||
| -1 | -1 | 37,66667 | 37,66667 | 37,66667 | 37,66667 | 37,66667 | ||||||
| -1 | -1 | |||||||||||
| -1 | 29,33333 | 29,33333 | 29,33333 | 29,33333 | 29,33333 | |||||||
| -1 | -1 | 23,33333 | 23,33333 | 23,33333 | 23,33333 | 23,33333 | ||||||
| -1 | ||||||||||||
| -1 | 27,66667 | 27,66667 | 27,66667 | 27,66667 | 27,66667 | |||||||
| 21,33333 | 21,33333 | 21,33333 | 21,33333 | 21,33333 | ||||||||
| 39,66667 | 39,66667 | |||||||||||
| -1 | 61,33333 | 61,33333 | ||||||||||
| -1 | 46,33333 | 46,33333 | ||||||||||
| 43,33333 | 43,33333 | |||||||||||
| -1 | ||||||||||||
| -1 | 41,33333 | 41,33333 | ||||||||||
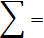| | 891,666 | 664,6667 |
Таблица 6 – Данные для расчёта коэффициентов
| № | | | | | |  |  |  |  |  |  |
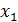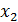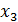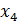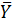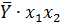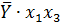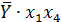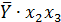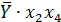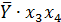| -1 | -1 | -1 | -1 | 51,33333 | 51,33333 | 51,33333 | 51,33333 | 51,33333 | 51,33333 | 51,33333 | |
| -1 | -1 | -1 | 56,66667 | 56,66667 | 56,66667 | -56,6667 | 56,66667 | -56,6667 | -56,6667 | ||
| -1 | -1 | -1 | -32 | -32 | -32 | ||||||
| -1 | -1 | -58 | -58 | -58 | -58 | ||||||
| -1 | -1 | -1 | 19,66667 | -19,6667 | 19,66667 | 19,66667 | -19,6667 | -19,6667 | 19,66667 | ||
| -1 | -1 | -49 | -49 | -49 | -49 | ||||||
| -1 | -1 | 38,66667 | -38,6667 | -38,6667 | 38,66667 | 38,66667 | -38,6667 | -38,6667 | |||
| -1 | -27 | -27 | -27 | ||||||||
| -1 | -1 | -1 | -54 | -54 | -54 | ||||||
| -1 | -1 | 37,66667 | -37,6667 | -37,6667 | 37,66667 | 37,66667 | -37,6667 | -37,6667 | |||
| -1 | -1 | -22 | -22 | -22 | -22 | ||||||
| -1 | 29,33333 | -29,3333 | 29,33333 | 29,33333 | -29,3333 | -29,3333 | 29,33333 | ||||
| -1 | -1 | 23,33333 | 23,33333 | -23,3333 | -23,3333 | -23,3333 | -23,3333 | 23,33333 | |||
| -1 | -16 | -16 | -16 | ||||||||
| -1 | 27,66667 | 27,66667 | 27,66667 | -27,6667 | 27,66667 | -27,6667 | -27,6667 | ||||
| 21,33333 | 21,33333 | 21,33333 | 21,33333 | 21,33333 | 21,33333 | 21,33333 | |||||
| 39,66667 | |||||||||||
| -1 | 61,33333 | ||||||||||
| -1 | 46,33333 | ||||||||||
| 43,33333 | |||||||||||
| -1 | |||||||||||
| -1 | 41,33333 | ||||||||||
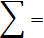| | 891,6667 | -9,66667 | -71,6667 | -18,3333 | 4,333333 |
Выполнение критериальных проверок
Проверим значимость коэффициентов полученной квазилинейной модели с целью исключения из модели факторов, слабо влияющих на функцию отклика.
Вычислим дисперсию наблюдения:
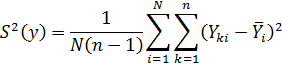
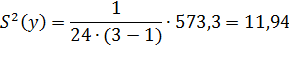
Дисперсии оценки коэффициентов 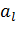модели:
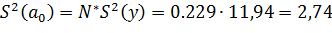
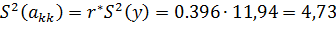
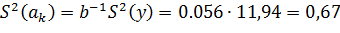
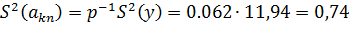
При количестве опытов в плане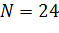 
и количестве повторных опытов 
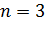число степеней свободы равно 
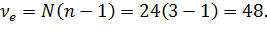Выбираем доверительную вероятность 
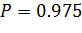и определяем по таблице из приложения 1 значение коэффициента Стьюдента 
.
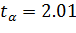Доверительный интервал коэффициентов аl модели
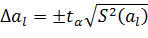
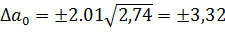
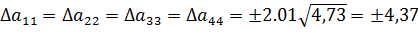
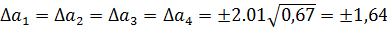
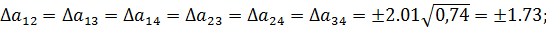
Коэффициент 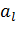модели значим, если абсолютная величина больше доверительного интервала, т.е. 
.
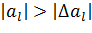Окончательный вид модели:
