Орнықтылық анықтамалары
Жүйені стандартты Xs күйінен қоздырушы әсерлер үздіксіз ауытқытатын болады, яғни (5.2) және (5.4) теңдеулері жағдайындағы координаталар басынан. Мұндай ауытқуларға жүйе қалай жауап беретіндігін анықтау қажет.
Жағдай 1. Барлық уақыт мезгілдерінде күй айнымалысы X(t)өзгеуі стандартты күй Xs белгілі бір маңайында қалатын болады. Дәлірек айтқанда, кез келген алдын ала берілген шама ε > 0 үшін сондай δ > 0 табылатын болса, жалпы жағдайда ε және t0 тәуелді (яғни δ(ε, t0)) және алғашқы қоздырулар x(t0) табылған шама δ аспаған кезде, ауытқу x(t) барлық уақыттарда ε кіші болып қалады.
Анықтама 1. Теңдеу (5.4) шешімімен анықталатын қоздырылмған қозғалыс Xs(t) Ляпунов бойынша орнықты болады, егер кез келген нақтылы ε > 0 үшін сондай аз нақтылы сан δ(ε, t0) > 0 табылатын болып
|x0| ≤ δ(ε, t0)
болған кезде, барлық t ≥ t0 үшін теңсіздік
|x(t)| ≤ ε
орындалатын болса (әрқашан ε ≥ δ). Немесе теңсіздік
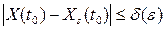
шығады, кез келген t > t0 уақыт мезгілінде теңсіздік
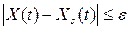
орындалатындығы.
Жағдай 2. Уақыт шексіздікке ұмтылған сайын, Х(t) күйі стандартты Xs күйіне ұмтылады немесе басқаша айтқанда, x(t) қоздыруы уақыт өткен сайын нольге ұмтылады. Онда Xs күйі асимтотикалық орнықты болады деп айтамыз (сурет 5.2).
Анықтама 2. Теңдеу (5.4) шешімімен анықталатын Xs(t)қоздырылмаған қозғалысы асимтотикалық орнықты деп аталады, егер
1) ол орнықты болса;
2) әр қозғалыс, жеткілікті жақын басталатын Xs уақыт t шексіздікке ұмтылған кезде (яғни 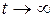 ) нольге ұмтылса
) нольге ұмтылса
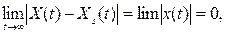
немесе
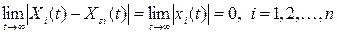 .
.
 a) a) | 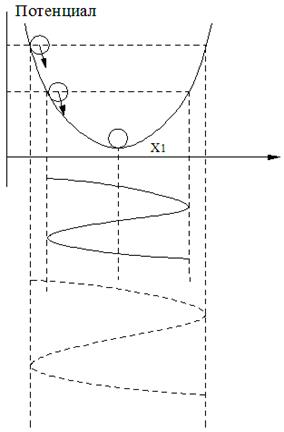 б) б) |
 в) в) |
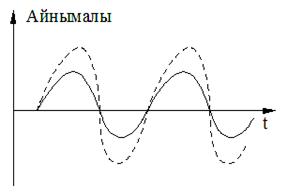
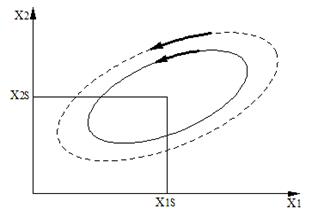
Сурет 5.1 – Ляпунов бойынша орнықтылыққа үш көзқарас: сурет 5.1а – стандартты Xs күйінің ауытқуы барлық уақытта шектеулі қалады; сурет 5.1б – материалдық нүктенің потенциалдық шұңқырдағы қозғалысы үшін әртүрлі екі алғашқы мән көрсетілген; сурет 5.1в – фазалық кеңістікте әртүрлі екі қоздыруға сәйкес стандартты (x1s, x2s) күй орбиталары көрсетілген.
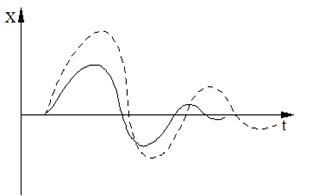
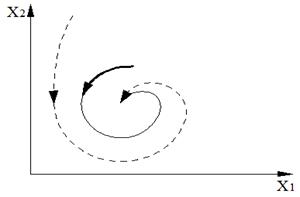
Сурет 5.2 – Асимптотикалық орнықтылық туралы екі көрсетілу: а) Х күй айнымалысының уақыт бойынша өзгеруі; б) аттракторға қосылатын фазалық траекториялар
Жағдай 3. X(t) күйі қоздырылмаған қозғалыс Xs маңында қалмайды. Дәлірек айтқанда, Xs әр аймағы үшін сондай алғашқы қоздыру бар болады, ол үшін X(t) амплитудасы әр уақытта, алдын ала еркін берілген шама ε0 үнемі кіші болып қала алмайды. Онда Xs қоздырылмаған (стационарлық) күйі орнықсыз деп айтамыз (сурет 5.3).
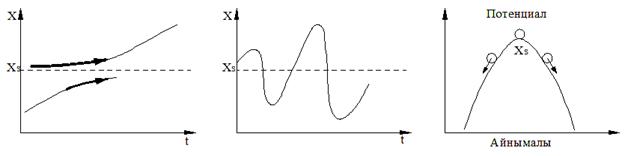
Сурет 5.3
Жағдай 4. X(t) күйі стандартты Xs күйінің белгілі бір аймағында қалатын болады, егер қоздырушы әсер белгілі бір деңгейдегі мәннен аспаса және қоздырушы бұл деңгейден асқан жағдайда Xs алшақтайды (қашықтайды). Онда Xs күйі локальды орнықты, бірақ глобальды орнықсыз деп айтамыз. Басқа жағынан, егер орнықтылық, алғашқы қоздырулардың кез келген амплитудасында орын алса, онда глобальды орнықтылық туралы айтамыз, сонымен қатар Xs күйі бұл жағдайда глобальды аттрактор болады (сурет 5.4).
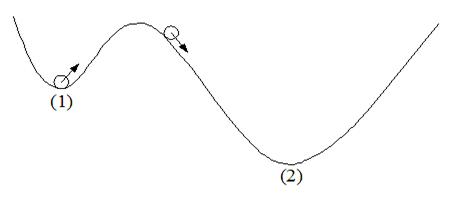
Сурет 5.4 – Глобальдық және локальдық орнықтылықтарға түрлендіру. Шар, ойыс (1) жылжып келе жатқан, онда қалуы мүмкін немесе ойыс (2) өтіп кетуі мүмкін, оның алғашқы кинетикалық энергиясы аз немесе соңғы өтпелі деңгейден асуына жеткілікті болуына байланысты.
Жалпы, бейсызықты стационарлық емес жүйелер үшін орнықтылықтың көптеген анықтамалары бар: тепе-теңдік нүктенің орнықтылығы және қозғалыстың орнықтылығы; Ляпунов бойынша орнықтылық және асимптотикалық орнықтылық; «кішкенедегі» және «үлкендегі» орнықтылық; бастапқы шарт бойынша орнықтылық және қоздырушы әсер бойынша орнықтылық. Сызықтық стационарлық жүйелер үшін бұл анықтамалардың барлығы да дәл түйіседі және мұндай жүйелер үшін жай ғана орнықтылық жөнінде айтатын боламыз.
