Кирхгофтың екінші заңы бойынша 4 страница

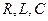параметрлар және кернеу 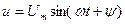берілген болсын, ал ізденіп жатқан шама – тоқ.

(3.7) дифференциалды теңдеудің шешуі синусоидалды функцияны береді,

,

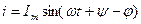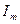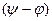мұнда және -тоқтың әлі белгісіз амплитудасы және басты фазасы, берілген синусоидалы кернеуге комплексті функция 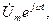ал ізденіп жатқан синусоидалды тоққа-комплексті функция 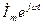сәйкесті болады.

Онда (4.7) теңдеуді мына түрде көрсетуге болады,

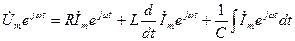(3.8)

Дифференциалдайды және интегралдауды өткізіп, табамыз;

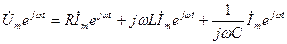(3.9)

(3.9) теңдеудің барлық бөліктерін көбейткіш 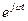қысқартып алгебралық комплексті теңдеуді табамыз:

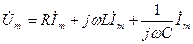(3.10)

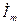тоқты жақшаның сыртына шығарғанда, болады:

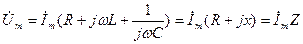(3.11)

мұнда 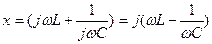-реактивтік кедергі; (3.12)

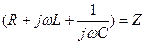-комплексті толық кедергі (3.13)

(3.11) теңдеудің екі жағы бөлсек, комплексті әсерлік мәндер үшін Омның заңын шығарамыз,

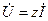(3.14)

Комплексті кедергіні тригонометриялық және көрсеткіш түрлері,

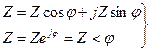(3.15)

мұнда 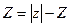-комплексті санның модулі, ал 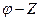комплексті санның аргументі,

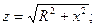
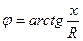(3.16)

(3.11) теңдеу бойынша тоқтың комплексті амплитудасы

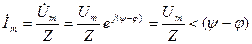
мұнда 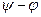-тоқтың басты фазасы.

Олай болса, ізденіп жатқан тоқ тригонометриялы түрде

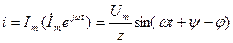(3.17)

бұл бұрынғы табылған (2.35) теңдеумен бірдей болып шықты яғни нәтижелерді бір-бірімен толық біртектес.

3.4-суретте (3.13) теңдеудің комплекті жазықтықта геометриялық талдау берілген. 3.4,а-сурет тізбектің реактивтік кедергісі индуктивтік түріне жатады 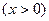, ал оған сәйкес тоқ кернеуден фаза бойынша қалып қалады 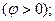3.4,б-сурет тізбектің реактивтік кедергісі сыйымдылық түріне жатады 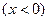, ал оған сәйкес тоқ кернеуден фаза бойынша озып кетеді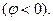

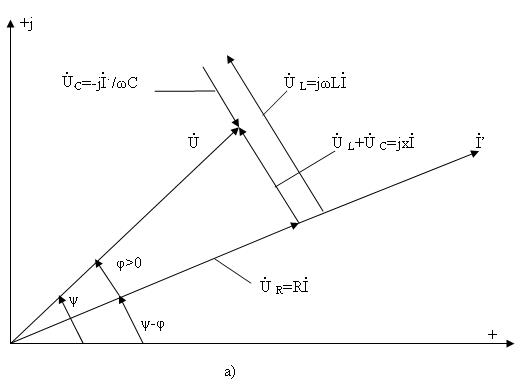
3.4-сурет. (а) және 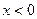(b) кезде 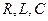тізбекті қосылған

үшін векторлық диаграммалар.

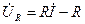кедергідегі кернеу ( 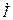тоқпен біртектес), 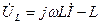индуктивтіктегі кернеу ( 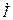тоқтан 90° бұрышқа қалып қалады).

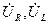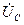және векторлардың геометрикалық қосындысы тізбекке ынта салынған кернеудің векторын береді:

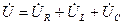
Катеттері 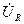және 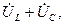гипотенузасы 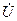-ға тең тұра бұрышты – кернеулер ұшбұрышы деп аталады.

б) 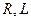және 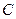-нің параллельді қосылуы.

Кирхгофтың бірінші заңына сәйкесті комплексті әсерлік мәндер үшін жазамыз:

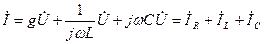(3.18)

мұнда 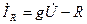кедергідегі тоқ ( 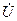кернеумен фаза бойынша біртектес);

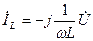-индуктивтіктегі тоқ (кернеуден 90° қалады);

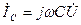-сыйымдылықтағы тоқ (кернуден 90° озады).

Көрініс

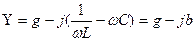(3.19)

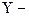қаралып жатқан тізбектің комплексті өткізгіштігі; және 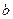-тізбектің активтік және реактивтік өткізгіштері.

Теңдеу

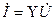(3.20)

Омның заңын комплексті түрде көрсетеді.

Комплексті өткізгіштіктің тригонометриялық және көрсеткіш түрлері,

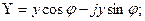
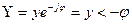(3.21)

мұнда 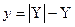комплекс санның модулі, ал 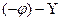комплекс санының аргументі.

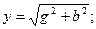
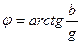(3.22)

(3.20) теңдеу бойынша тоқтың комплексті амплитудасы,

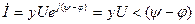
ал бұл мынадай синусоидалды тоққа сәйкес,

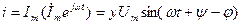(3.23)

3.5-суретте (3.17) теңдеудің комплекстік жазықтықта геометрикалық талдау берілген. 3.5,а-сурет тізбектің реактивтік өткізгіштігі индуктивтік түріне жатады 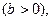ал оған сәйкес тоқ кернеуден фаза бойынша қалып қалады 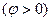; 3.5,б-сурет тізбектің реактивтік өткізгіштігі сыйымдылық түріне жатады ал оған сәйкес тоқ кернеуден фаза бойынша озып кетеді

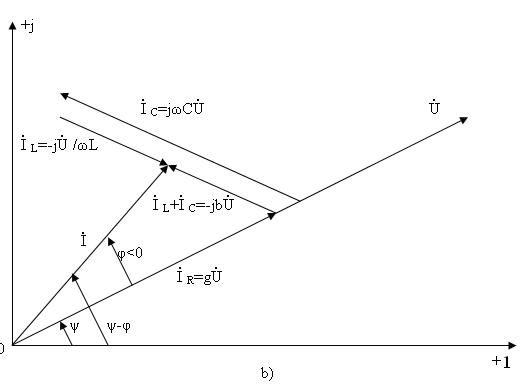
3.5-сурет. (а) және (б) кезде параллельді қосылған тізбек үшін векторлық диаграммалар.

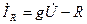кедергідегі тоқ ( 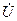кернеумен біртектес); 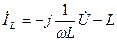индуктивтіктегі тоқ ( 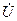кернеуден 90° қалып қалады); 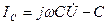сыйымдылықтағы тоқ ( 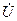кернеуден 90° озып кетеді).

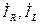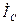және векторлардың геометриялық қосындысы тізбектегі жалпы тоқ 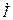-дің векторын береді:

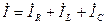
Катеттері 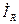және 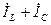, гипотенузасы 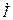-ға тең тұра бұрышты ұшбұрыш – тоқтардың ұшбұрышы.

Егер де тізбектің бөлігінің комплексті кедергісі берілсе, онда сол бөлігінің комплексті өткізгіштігі тең:

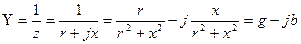(3.24)

Егер де тізбектің бөлігінің комплесті өткізгіштігі берілсе, онда сол бөлігінің комплексті кедергісі тең:

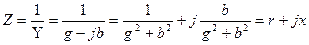(3.25)

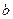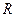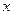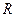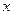Өткізгіштің әрбір қосындысына ( және ) активтік кедергі -ға және реактивті кедергі -ке тәуелді, ал кедергі әрбір қосындысы ( және ) активтік өткізгіштік -ға және реактивтік өткізгіштік -ға тәуелді.

3.3 Комплекстік түрдегі электрлік қуат

Тізбек арқылы синусойдалды тоқ өтіп жатыр және тоқтың бағытымен кернеудің бағыты біртектес (3.6-сурет)

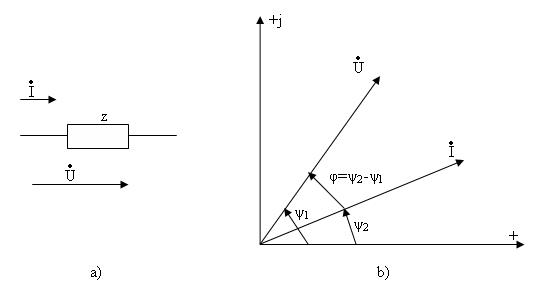
3.6-сурет. Тоқ және кернеудің болымды бағыттары (а) және векторлық диаграммасы (b).

Комплексті тоқ және кернеу тең:

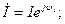
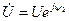
Тоқтың кернеуге қарай фазалық ығысу басты фазалардың айырымына тең:

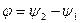
Кернеудің комплексін 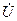тоқ 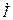-мен түйіндес 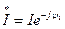комплекстік мәнге көбейтеміз,

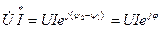
Бұдан комплекстік қуат шығады:

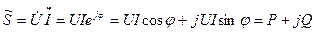(3.26)

Сонымен, 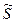комплекстік мәннің нақты бөлігі активтік қуатты белгілейді, ал жорамал бөлігі тізбекке түсетін реактивтік қуатты белгілейді.

Комплекстік қуаттың модулі 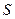толық қуатқа тең.

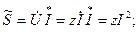
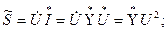
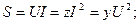
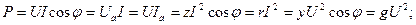
3.4 Потенциалды (типографиялық) диаграмма

Бұл диаграмма берілген тізбектің потенциалы нөлге тең бір нүктеге қарай бөлек нүктелерді комплекстік потенциалдары салынған. Кернеу түсуі векторлардың орналасу тәртібі диаграммада сұлбадағы тізбек элементтер орналасу тәртібіне қатал сәйкес. Әрбір кейінгі элементің кернеу векторына аяғы алдынғы элементтің кернеу векторының басына жалғасады. Бұлай кернеулердің векторлық диаграммасын құрғанда электр тізбектің әрбір нүктесіне потенциалды диаграммада белгілі нүкте сәйкес.

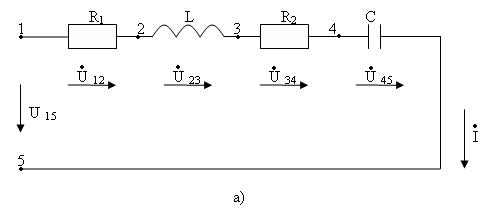
3.7(а) -сурет. Тізбектің сүлбесі

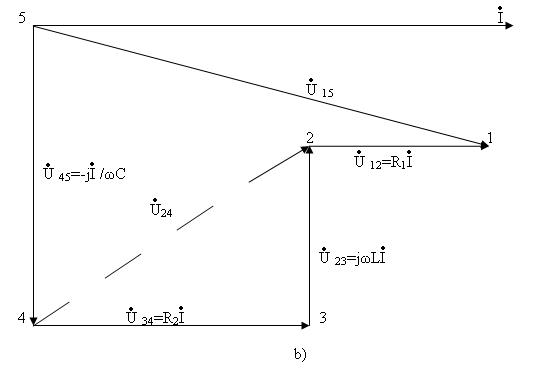
3.7-сурет. Тізбектің сүлбесі (а) және потенциалды диаграммасы (b).

Сүлбені айналып өту тоқтың болымды бағытына қарсы.

Сүлбеде элементтердің орналасу тәртібіне сәйкес диаграммада кернеулердің векторлары бейнелеген:

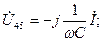
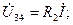
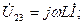
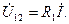
Векторлардың басы мен аяқтары (3.7,b-сурет) сүлбеде алынған (3.7,а-сурет) нүктелердің нөмірлеріне сәйкес номерленген.

Сүлбенің қандайда болған екі нүктенің арасындағы кернеу, мысалы, сүлбенің 2-4 бөлігінде потенциалдық диаграммада диаграмманың 2 және 4 нүктелерін қосатын және диаграммада 4 нүктеден 2 нүктеге бағытталған 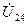векторымен белгіленеді.

Сонымен, диаграммада кернеу векторы жоғары (азайтылған) потенциалы бар нүктеге бағытталады, ал сүлбеде кернеу жоғары потенциалы бар нүктеден төмен потенциалы бар нүктеге қарай бағытталған тілімен көрсетіледі.

Төртінші тарау

4 Электр тізбектердегі резонанс

4.1 Тармакталмаған тізбектегі резонанс (кернеулер резонансы)

Индуктивтік орауыштары және конденсаторлары бар тізбектерде кіріс кедергісі немесе кіріс өткізгіштігі нөлге тең болғандағы ережені резонанас деп атайды.

Кернеулер резонансы индуктивтігі және сыйымдылығы бар тізбектеп қосылған участіктерден құралған электр тізбекте байқалады.

Кернеулер резонансы кезде тізбектің бір бөлігінде индуктивтік кедергі онымен тізбектеп қосылған бөлігінде сыйымдылық кедергімен өтемделеді. Бұның нәтижесінде тізбектегі реактивтік кедергі және реактивтік қуат нөлге тең болады.

Элементтер тізбектеп қосылған тізбекті (4.1-сурет) жиі тербелмелі контур деп атайды.

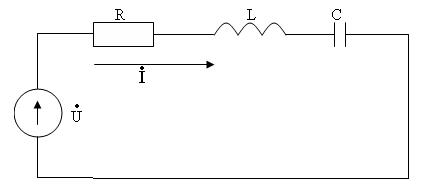
4.1-сурет. Тізбекті тербелмелі контур.

Мұндай тізбектің комплекстік кедергісі жиіліктен тәуелді:

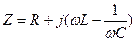(4.1)

Кернеулер резонансы орнатылады егер де мындай теңдік болса

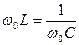(4.2)

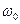-резонанстық бұрыштық жиілік, оның шамасы (4.2) теңдеуден тең:

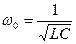(4.3)

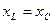кезде индуктивтіктегі және сыйымдылықтағы фаза бойынша қарсы кернеулердің мәндері бір-біріне тең (4.2-сурет), сондықтан кернеулер резонансы деп атайды.

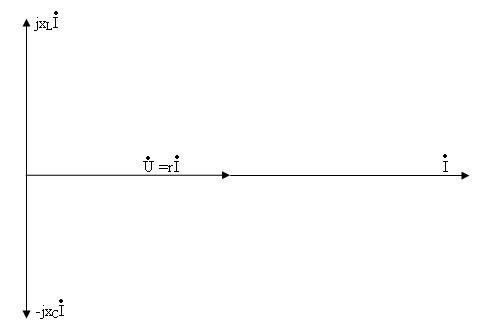
4.2-сурет. Кернеулер резонанстың векторлық диаграммасы.

Резонанс ережеге жету үшін көздің жиілігі немесе тізбектің параметрлерін ( 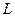немесе 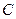) өзгерту керек.

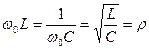(4.4)

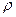-тізбектің (контурдың) сипаттамалық кедергісі деп аталады.

Индуктивтіктегі немесе сыйымдылықтағы кернеудің резонанас кезінде тізбекке ынта салған кернеуге қатынасын:

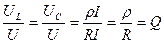(4.5)

конурдың сапалығы немесе резонанстың коэффициенті деп атайды.

Резонанс кезде толық кедергі 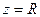, ал тізбектің қысқыштарындағы кернеу активтік кедергідегі кернеуіне тең. Сол себептен тоқ берілген 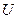кернеу кезде өте үлкен 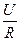мәнге жетеді. Сонымен бірге индуктивтіктегі және сыйымдылықтағы кернеулер резонанс кезде тізбектің қысқыштарындағы кернеуден едәуір үлкен болды.

Тізбектің магнит және электр өрістердің қосынды энергиясы резонанс кезде тең:

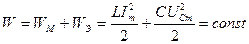, (4.6)

яғни магнит және электр өрістердің энергиясы уақыт бойынша өзгермейді. Электр өрістің энергиясының азаюы магнит өрістің энергиясының үлкеюімен өтеді және керсінше.

Тізбекке (4.1-сурет) кернеу 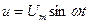салынып тұр. Оның амплитудасы тұрақты, ал жиілігі -ден -ке дейін шектерде өзгеріп тұр.

Жиіліктің өзгеруі тізбектің параметрлерін өзгертеді, яғни реактивтік кедергіні және 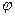бұрышын (комплекстік кедергінің аргументі).

Тізбектің параметрлерінің жиіліктен тәуелділіктері тізбектің жиілік сипаттамалары деп, ал тоқтың және кернеудің мәндерінің жиіліктен тәуелділіктері – резонанстық қисықтар деп аталады.

4.3-суретте жиілік сипаттамалар, ал 4.4-суретте резонанстық қисықтар көрсетілген.

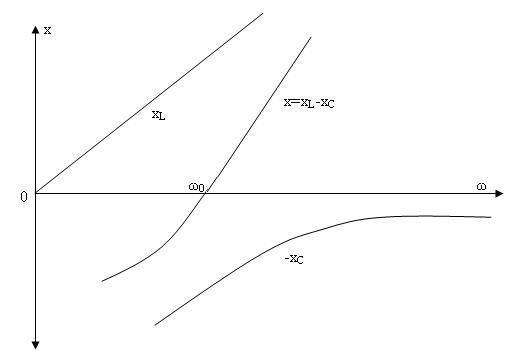
4.3-сурет. Жиілік сипаттамалар.

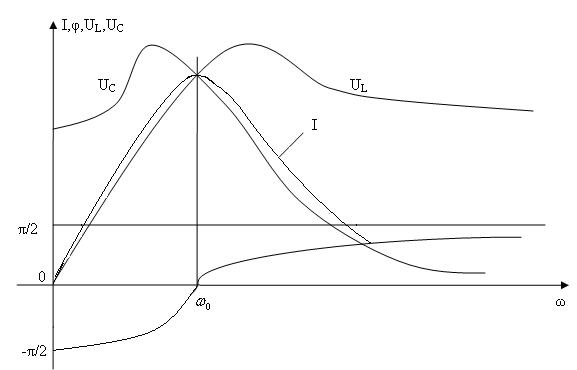
4.4-сурет. Резонанстық қисықтар.

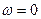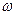
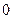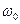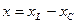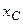
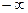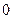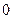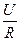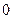кезде кернеу уақат бойынша өзгермейді, сондықтан тоқ нөлге тең. Жиілік -ден -ге дейін өзгергенде сыйымдылық түрлі болады да -ден -ге дейін өзгереді. Сондықтан тоқ -ден ең үлкен мәнге дейін өседі, ал кернеумен тоқтың арасындағы фаза ығысу -ден -ге дейін өзгереді.

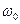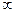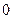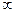Жиілік -ден -ге дейін өскенде реактивтік кедергі -ден -ге дейін өседі және индуктивтік түрлі болады. Соның салдарынан, тоқ максималды мәннен 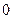-ге дейін азаяды, ал бұрыш 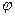нөлден 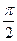-ге дейін үлкееді.

Индуктивтіктегі кернеу 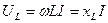, яғни екі көбейткіште жиілікке тәуелді. Жиілік 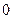-ден 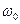-ге дейін өзгергенде кернеу 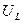өседі.

Сыйымдылықтағы кернеу 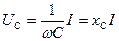. Жиілік 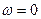кезде тоқ жоқ, сондықтан 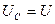. Жиілік 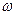нөлден өскенде 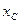өне бойы төмендейді. Кернеу 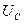алдымен өседі де 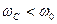кезде максимумға жетеді, себебі тоқ өседі. Содан кейін 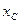азайғандықтан 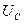төмендейді, 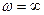кезде 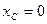, ал сол себептен .

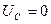4.2 Тармакталған тізбектегі резонанс (тоқтардың резонансы)

Екі параллельді тармақтары бар: біреуі – кедергімен және индуктивтікпен, екіншісі-кедергімен және сыйымдылықпен тізбекті қосылған сүлбені қарап шығайық.(4.4-сурет).