Gо to 1

шагm_D

20 х_i = х_i + 1

y_i = y_i + 1

_i = _i+ 2х_i - 2у_i+ 2

Gо to 1

Finish

Переменная предела устанавливается в нуль для окончания работы алгоритма на горизонтальной оси, в результате генерируется окружность в первом квадранте. Если необходим лишь один из октантов, то второй октант можно получить с помощью установки Предел =Integer (R/sqrt(2)), а первый - с помощью отражения второго октанта относительно прямой у = х (рис. 5.1). Блок-схема алгоритма приводится на рис. 5.5.

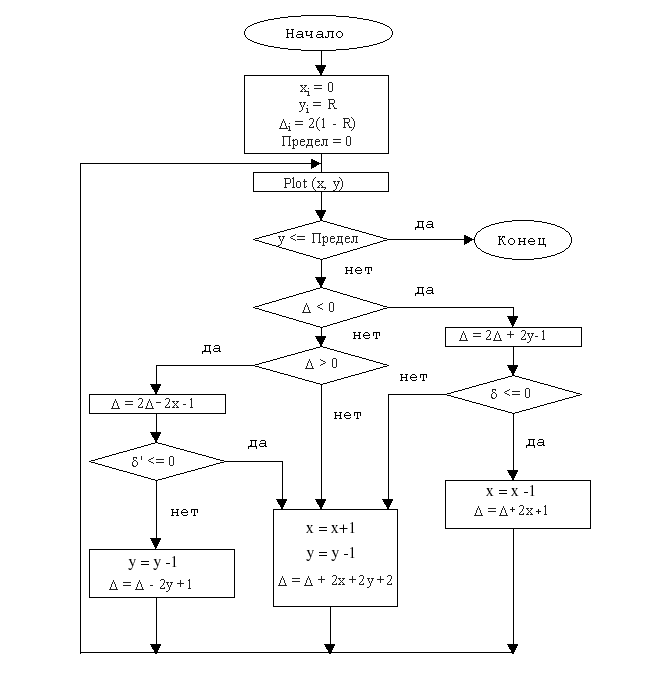Рис. 5.5. Блок-схема пошагового алгоритма Брезенхема для генерации окружности в первом квадранте.

Пример 5.1. Алгоритм Брезенхема для окружностию

Рассмотрим окружность радиусом 8 с центром в начале координат. Генерируется только первый квадраннт.

начальные установки

x = 0

y = 8

= 2(1-8) = -14

Предел = 0

Пошаговое выполнение основного цикла

1 Plot (0,8)

yi > Предел (продолжать)

i < 0 go to 2

2 go to 10

10 x = 0+1 = 1

i = -14 +2 + 1 = -11

go to 1

1 Plot (1,8)

yi > Предел (продолжать)

i < 0 go to 2

2 go to 10

10 x = 1+1 = 1

i = -11 +2(2) + 1 = -6

go to 1

1 Plot (2,8)

...

Продолжать

Результаты всех последовательных проходов алгоритма сведены в таблицу. Список пикселов выбранных алгоритмов состоит из (0,8), (1,8), (2,8), (3,7), (4,7), (5,6), (6,5), (7,4), (7,3), (8,2), (8,1), (8,0).

Plot	i		'	x	y
	-14
(0,8)
	-11	-13
(1,8)
	-6	-7
(2,8)
	-12
(3,7)
	-3
(4,7)
	-3
(5,6)
(6,5)
			-11
(7,4)
(7,3)
			-7
(8,2)
(8,1)
(8,0)

алгоритм завершен.

Результаты показаны на рис.5.6. вместе с реальной окружностью. Алгоритм легко обобщается для других квадрантов или дуг окружностей.

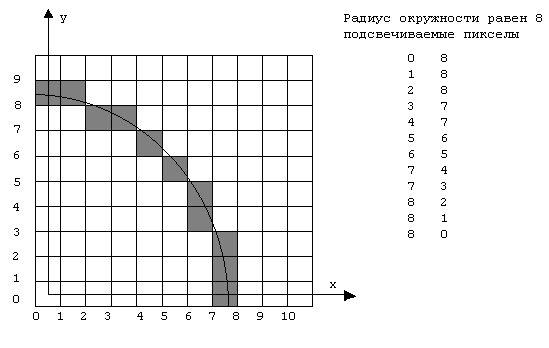Рис. 5.6. Результаты работы пошагового алгоритма Брезенхема генерации окружности.