Обеспечение устойчивости решения системы нормальных уравнений при плохо обусловленной информационной матрице

По экспериментальным данным из приложения 3 методом наименьших квадратов найти оценки регрессионных коэффициентов регрессионной модели 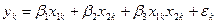и сравнить их с истинными значениями, приведенными в приложении 3.

Проверить наличие мультиколлинеарности, вычислив меру обусловленности матрицы нормальной системы уравнений. Найти корреляционную матрицу и установить источник мультиколлинеарности.

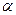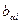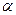Используя метод регуляризации, установить мультиколлинеарность. Для определения параметра регуляризации построить гребневый след – график зависимости оценок от . Указать значение параметра 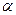, при котором оценки стабилизируются.

С учетом истинных значений регрессионных коэффициентов, приведенных в приложении 3, построить зависимость квадратичной ошибки оценок коэффициентов от параметра регуляризации 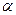и найти оптимальное значение параметра регуляризации.

Указать оценки регрессионных коэффициентов, соответствующих оптимальному значению параметра регуляризации, сравнить их с истинными значениями и оценить погрешности.

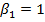
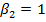
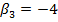
Таблица 1

k	x1k	x2k	yk
	-1	-1,971	-10,908
	-0,765	-1,511	-6,859
	-0,530	-1,063	-4,057
	-0,295	-0,6	-1,537
	-0,060	-0,114	-0,198
	0,175	0,344	0,587
	0,410	0,833	-0,340
	0,645	1,274	-1,310
	0,880	1,763	-3,531
		2,003	-5,036

Решение:

Матрица регрессоров имеет вид:

	-1	-1,971	1,971
	-0,765	-1,511	1,155915
	-0,530	-1,063	0,03339
	-0,295	-0,6	0,177
F=	-0,060	-0,114	0,00684
	0,175	0,344	0,0602
	0,410	0,833	0,34153
	0,645	1,274	0,82173
	0,880	1,763	1,55144
		2,003	2,003

	-1	-0,765	-0,53	-0,295	-0,06	0,175	0,41	0,645	0,88
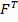=	-1,971	-1,511	-1,063	-0,6	-0,114	0,344	0,833	1,274	1,763	2,003
	1,971	1,155915	0,56339	0,177	0,00684	0,0602	0,34153	0,82173	1,55144	2,003

Информационная матрица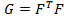

4,3459	8,652045	0,842348
8,652045	17,22641	1,761993
0,842348	1,761993	12,78425

Матрица дисперсий ковариаций C= :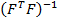

4448,534	-2235,84	15,04297
-2235,84	1123,792	-7,56872
15,04297	-7,56872	0,130208

	-12,051	-7,392	27,446	31,847	-11,924	10,271	-33,415	33,210	-3,731	0,285
C 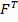=	5,925	3,617	-13,861	-16,043	5,986	-5,143	16,841	-16,623	1,966	-0,042
	0,132	0,079	0,146	0,127	-0,039	0,037	-0,093	0,167	0,096	0,144

МНК оценки коэффициентов регрессионной модели

9,840

-3,428

-3,986

Модель принимает вид

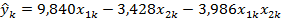
Сравним полученные оценки b с истинными значениями 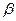, вычислив относительные погрешности:

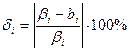
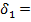884% 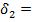442,8% 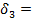0,35%

Как видно, оценки b₁, и b₂ несут на себе непозволительно большую погрешность, которая серьезно исказит предсказанные по модели значения. Попробуем это исправить. Для начала проверим наличие мультиколлинеарности, вычислив меру обусловленности матрицы 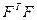, которая является правой частью в системе уравнения МНК.

Выберем норму вида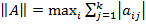

Мера обусловленности матрицы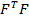

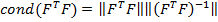= 27,64044* 2227,741= 61575,74

Слишком большое значение меры обусловленности свидетельствует о плохой обусловленности информационной матрицы. Установим ее источник. Стандартизируем регрессионную модель, чтобы потом вычислить ее корреляционную матрицу R.

Процесс стандартизации для элементов матрицы F и y_k выглядит следующим образом:

, , ,

, , .

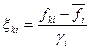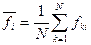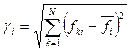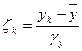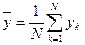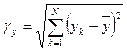В результате получим значения, приведенные в таблице:

k	ξ1k	ξ 2k	ξ 3k	ζk
	-0,503	-0,499	0,480	-0,708
	-0,390	-0,388	0,126	-0,330
	-0,277	-0,280	-0,131	-0,069
	-0,164	-0,168	-0,299	0,166
	-0,051	-0,051	-0,373	0,291
	0,062	0,060	-0,350	0,365
	0,175	0,178	-0,228	0,278
	0,288	0,285	-0,019	0,188
	0,401	0,403	0,298	-0,020
	0,459	0,461	0,494	-0,160

	-0,503	-0,390	-0,277	-0,164	-0,051	0,062	0,175	0,288	0,401	0,459
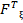=	-0,499	-0,388	-0,280	-0,168	-0,051	0,060	0,178	0,285	0,403	0,461
	0,480	0,126	-0,131	-0,299	-0,373	-0,350	-0,228	-0,019	0,298	0,494

Вычислим корреляционную матрицу.

		0,999963	0,092827
R=	0,999963		0,097933
	0,092827	0,097933

Таким образом, источником мультиколлинеарности является сильная корреляция между ξ_1k и ξ_2k ил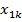и и 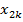. det R= 0,00005.

Устраним мультиколлинеарность, применив метод регуляризации.

Регуляризованные оценки вычисляются по формуле

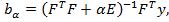
где α – параметр регуляризации.

Определим его двумя способами, предварительно составив таблицу, в которой приведем значения 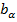и значения квадратичной ошибки регрессионных коэффициентов в зависимости от α. Последнюю можно вычислить по формуле:

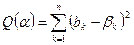
Первый способ определения параметра регуляризации предусматривает построение «гребневого следа» (графика зависимости 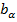от α) и определения по нему значения α, при котором оценки стабилизируются.

alpha	b1	b2	b3	Q
	9,840468	-3,42836	-3,986	97,76448
0,001	2,022663	0,500809	-4,01211	1,295179
0,002	1,3789	0,824264	-4,01396	0,174644
0,003	1,140062	0,944202	-4,01444	0,022939
0,004	1,015495	1,006706	-4,01454	0,000496
0,005	0,939012	1,045044	-4,01447	0,005958
0,006	0,887269	1,070946	-4,01431	0,017946
0,007	0,849929	1,08961	-4,01411	0,03075
0,008	0,821708	1,103691	-4,01388	0,042732
0,009	0,799627	1,114685	-4,01362	0,053488
0,01	0,781876	1,123504	-4,01336	0,06301
0,011	0,767293	1,13073	-4,01308	0,071414
0,012	0,755098	1,136756	-4,01279	0,078843
0,013	0,744747	1,141855	-4,0125	0,085433
0,014	0,73585	1,146223	-4,0122	0,091305
0,015	0,728119	1,150005	-4,0119	0,096562

Построим графики для 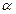из [0,002; 0,015]

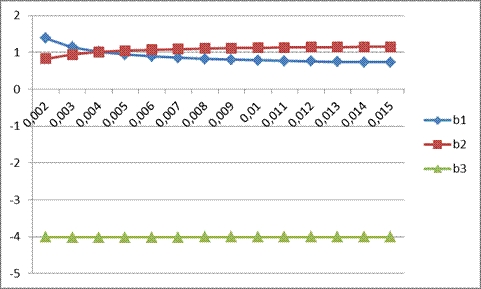
Как видно, оценки стабилизируются при α=0,008.

Найдем параметр регуляризации вторым способом, который заключается в поиске минимального значения квадратичной ошибки.

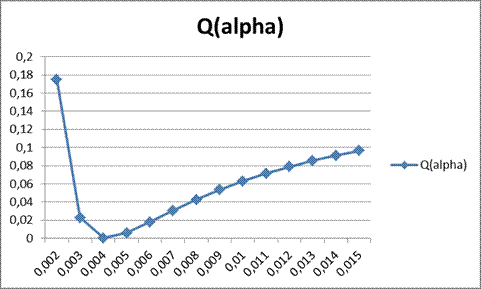
Таким образом, при α=0,004 получили наилучшие результаты регуляризации. Значит, данное значение α является оптимальным.

Запишем оценки регрессионных коэффициентов, соответствующие оптимальному значению параметра регуляризации α=0,004:

	1,015
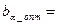	1,007
	-4,015

Модель будет иметь вид:

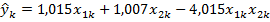
Сравним 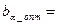с истинными значениями β, вычислив относительную погрешность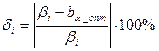

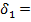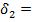1,5% 0,7% 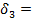0,735%

Видим значительное улучшение результатов по сравнению с результатами, полученными при оценивании коэффициентов простым МНК.