Линейные регрессионные модели с гетероскедастичными остатками
При оценке параметров уравнения регрессии применяется метод наименьших квадратов (МНК). При этом делаются определенные предпосылки относительно случайной составляющей 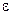 .
.
В модели
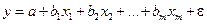
случайная составляющая 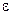 представляет собой ненаблюдаемую величину. После того как произведена оценка параметров модели, рассчитывая разности фактических и теоретических значений результативного признака y, можно определить оценки случайной составляющей
представляет собой ненаблюдаемую величину. После того как произведена оценка параметров модели, рассчитывая разности фактических и теоретических значений результативного признака y, можно определить оценки случайной составляющей 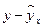 . Поскольку они не являются реальными случайными остатками, их можно считать некоторой выборочной реализацией неизвестного остатка заданного уравнения, т.е.
. Поскольку они не являются реальными случайными остатками, их можно считать некоторой выборочной реализацией неизвестного остатка заданного уравнения, т.е.  .
.
При изменении спецификации модели, добавлении в нее новых наблюдений выборочные оценки остатков  могут меняться. Поэтому в задачу регрессионного анализа входит не только построение самой модели, но и исследование случайных отклонений
могут меняться. Поэтому в задачу регрессионного анализа входит не только построение самой модели, но и исследование случайных отклонений  , т.е. остаточных величин.
, т.е. остаточных величин.
При использовании критериев Фишера и Стьюдента делаются предположения относительно поведения остатков  :
:
– остатки представляют собой независимые случайные величины и их среднее значение равно 0;
– они имеют одинаковую (постоянную) дисперсию;
– они подчиняются нормальному распределению.
После построения уравнения регрессии проводится проверка наличия у оценок  (случайных остатков) тех свойств, которые предполагались. Связано это с тем, что оценки параметров регрессии должны отвечать определенным критериям. Они должны быть несмещенными, состоятельными и эффективными. Эти свойства оценок, полученных по МНК, имеют чрезвычайно важное практическое значение в использовании результатов регрессии и корреляции.
(случайных остатков) тех свойств, которые предполагались. Связано это с тем, что оценки параметров регрессии должны отвечать определенным критериям. Они должны быть несмещенными, состоятельными и эффективными. Эти свойства оценок, полученных по МНК, имеют чрезвычайно важное практическое значение в использовании результатов регрессии и корреляции.
Несмещенность[1] оценки означает, что математическое ожидание остатков равно нулю. Если оценки обладают свойством несмещенности, то их можно сравнивать по разным исследованиям.
Оценки считаются эффективными, если они характеризуются наименьшей дисперсией. В практических исследованиях это означает возможность перехода от точечного оценивания к интервальному.
Состоятельность оценок характеризует увеличение их точности с увеличением объема выборки. Большой практический интерес представляют те результаты регрессии, для которых доверительный интервал ожидаемого значения параметра регрессии 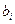 имеет предел значений вероятности, равный единице. Иными словами, вероятность получения оценки на заданном расстоянии от истинного значения параметра близка к единице.
имеет предел значений вероятности, равный единице. Иными словами, вероятность получения оценки на заданном расстоянии от истинного значения параметра близка к единице.
Указанные критерии оценок (несмещенность, состоятельность и эффективность) обязательно учитываются при разных способах оценивания. Метод наименьших квадратов строит оценки регрессии на основе минимизации суммы квадратов остатков. Поэтому очень важно исследовать поведение остаточных величин регрессии  . Условия, необходимые для получения несмещенных, состоятельных и эффективных оценок, представляют собой предпосылки МНК, соблюдение которых желательно для получения достоверных результатов регрессии.
. Условия, необходимые для получения несмещенных, состоятельных и эффективных оценок, представляют собой предпосылки МНК, соблюдение которых желательно для получения достоверных результатов регрессии.
Исследования остатков  предполагают проверку наличия следующих пяти предпосылок МНК:
предполагают проверку наличия следующих пяти предпосылок МНК:
1) случайный характер остатков;
2) нулевая средняя величина остатков, не зависящая от 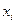 ;
;
3) гомоскедастичность – дисперсия каждого отклонения  , одинакова для всех значений x;
, одинакова для всех значений x;
4) отсутствие автокорреляции остатков – значения остатков  распределены независимо друг от друга;
распределены независимо друг от друга;
5) остатки подчиняются нормальному распределению.
Если распределение случайных остатков  не соответствует некоторым предпосылкам МНК, то следует корректировать модель.
не соответствует некоторым предпосылкам МНК, то следует корректировать модель.
Прежде всего, проверяется случайный характер остатков  – первая предпосылка МНК. С этой целью стоится график зависимости остатков
– первая предпосылка МНК. С этой целью стоится график зависимости остатков  от теоретических значений результативного признака (рис. 2.1). Если на графике получена горизонтальная полоса, то остатки
от теоретических значений результативного признака (рис. 2.1). Если на графике получена горизонтальная полоса, то остатки  представляют собой случайные величины и МНК оправдан, теоретические значения
представляют собой случайные величины и МНК оправдан, теоретические значения 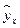 хорошо аппроксимируют фактические значения y.
хорошо аппроксимируют фактические значения y.
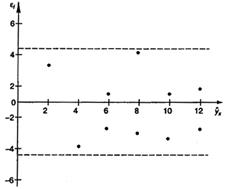
Рис. 2.1. Зависимость случайных остатков от теоретических значений .
Возможны следующие случаи, если  зависит от
зависит от 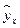 то:
то:
1) остатки  не случайны (рис. 2.2а);
не случайны (рис. 2.2а);
2) остатки  не имеют постоянной дисперсии (рис. 2.2б);
не имеют постоянной дисперсии (рис. 2.2б);
3) остатки  носят систематический характер (рис. 2.2в).
носят систематический характер (рис. 2.2в).
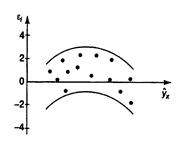 | 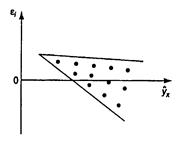 | 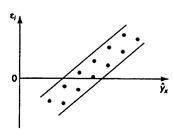 |
| а | б | в |
Рис. 2.2. Зависимость случайных остатков 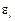 от теоретических значений от теоретических значений 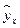 . . |
В этих случаях необходимо либо применять другую функцию, либо вводить дополнительную информацию и заново строить уравнение регрессии до тех пор, пока остатки  не будут случайными величинами.
не будут случайными величинами.
Вторая предпосылка МНК относительно нулевой средней величины остатков означает, что 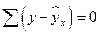 . Это выполнимо для линейных моделей и моделей, нелинейных относительно включаемых переменных.
. Это выполнимо для линейных моделей и моделей, нелинейных относительно включаемых переменных.
Вместе с тем, несмещенность оценок коэффициентов регрессии, полученных МНК, зависит от независимости случайных остатков и величин x, что также исследуется в рамках соблюдения второй предпосылки МНК. С этой целью наряду с изложенным графиком зависимости остатков  от теоретических значений результативного признака
от теоретических значений результативного признака 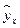 строится график зависимости случайных остатков
строится график зависимости случайных остатков  от факторов, включенных в регрессию
от факторов, включенных в регрессию 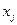 (рис. 2.3).
(рис. 2.3).
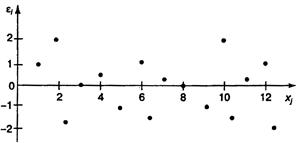
Рис. 2.3. Зависимость величины остатков от величины фактора .
Если остатки на графике расположены в виде горизонтальной полосы, то они независимы от значений 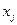 . Если же график показывает наличие зависимости
. Если же график показывает наличие зависимости  и
и 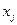 , то модель неадекватна. Причины неадекватности могут быть разные. Возможно, что нарушена третья предпосылка МНК и дисперсия остатков не постоянна для каждого значения фактора
, то модель неадекватна. Причины неадекватности могут быть разные. Возможно, что нарушена третья предпосылка МНК и дисперсия остатков не постоянна для каждого значения фактора 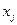 . Может быть неправильна спецификация модели и в нее необходимо ввести дополнительные члены от
. Может быть неправильна спецификация модели и в нее необходимо ввести дополнительные члены от 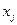 , например
, например 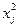 .
.
Предпосылка о нормальном распределении остатков позволяет проводить проверку параметров регрессии и корреляции с помощью F- и t-критериев. Вместе с тем, оценки регрессии, найденные с применением МНК, обладают хорошими свойствами даже при отсутствии нормального распределения остатков, т.е. при нарушении пятой предпосылки МНК.
Совершенно необходимым для получения по МНК состоятельных оценок параметров регрессии является соблюдение третьей и четвертой предпосылок.
В соответствии с третьей предпосылкой МНК требуется, чтобы дисперсия остатков была гомоскедастичной. Это значит, что для каждого значения фактора 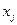 остатки
остатки  имеют одинаковую дисперсию. Если это условие применения МНК не соблюдается, то имеет место гетероскедастичность. Наличие гетероскедастичности можно наглядно видеть из поля корреляции (рис. 2.4).
имеют одинаковую дисперсию. Если это условие применения МНК не соблюдается, то имеет место гетероскедастичность. Наличие гетероскедастичности можно наглядно видеть из поля корреляции (рис. 2.4).
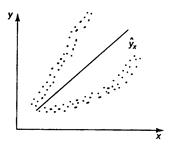 | 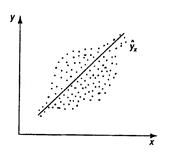 | 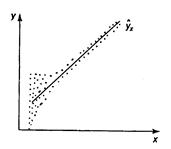 |
| а | б | в |
| Рис. 2.4. Примеры гетероскедастичности. |
На рис. 2.4 изображено: а – дисперсия остатков растет по мере увеличения x; б – дисперсия остатков достигает максимальной величины при средних значениях переменной x и уменьшается при минимальных и максимальных значениях x; в – максимальная дисперсия остатков при малых значениях x и дисперсия остатков однородна по мере увеличения значений x.
Наличие гомоскедастичности или гетероскедастичности можно видеть и по рассмотренному выше графику зависимости остатков  от теоретических значений результативного признака
от теоретических значений результативного признака 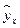 . Так, для рис. 2.4а зависимость остатков от
. Так, для рис. 2.4а зависимость остатков от 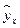 представлена на рис. 2.5.
представлена на рис. 2.5.
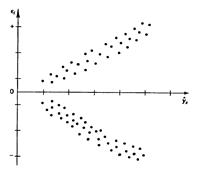
Рис. 2.5. Гетероскедастичность: большая дисперсия для больших значений .
Соответственно для зависимости, изображенной на полях корреляции рис. 2.4б и 2.4в, гетероскедастичность остатков представлена на рис. 2.6 и 2.7.
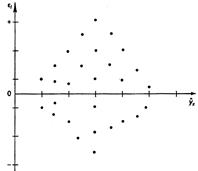
Рис. 2.6. Гетероскедастичность, соответствующая полю корреляции на рис. 2.4б.
Рис. 2.7. Гетероскедастичность, соответствующая полю корреляции на рис. 2.4в.
Для множественной регрессии данный вид графиков является наиболее приемлемым визуальным способом изучения гомо- и гетероскедастичности.
При построении регрессионных моделей чрезвычайно важно соблюдение четвертой предпосылки МНК – отсутствие автокорреляции остатков, т.е. значения остатков  , распределены независимо друг от друга. Автокорреляция остатков означает наличие корреляции между остатками текущих и предыдущих (последующих) наблюдений[2]. Коэффициент корреляции между
, распределены независимо друг от друга. Автокорреляция остатков означает наличие корреляции между остатками текущих и предыдущих (последующих) наблюдений[2]. Коэффициент корреляции между  и
и 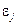 , где
, где  – остатки текущих наблюдений,
– остатки текущих наблюдений, 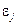 – остатки предыдущих наблюдений (например,
– остатки предыдущих наблюдений (например, 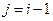 ), может быть определен как
), может быть определен как
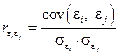 ,
,
т.е. по обычной формуле линейного коэффициента корреляции. Если этот коэффициент окажется существенно отличным от нуля, то остатки автокоррелированы и функция плотности вероятности 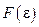 зависит от j-й точки наблюдения и от распределения значений остатков в других точках наблюдения.
зависит от j-й точки наблюдения и от распределения значений остатков в других точках наблюдения.
Отсутствие автокорреляции остаточных величин обеспечивает состоятельность и эффективность оценок коэффициентов регрессии. Особенно актуально соблюдение данной предпосылки МНК при построении регрессионных моделей по рядам динамики, где ввиду наличия тенденции последующие уровни динамического ряда, как правило, зависят от своих предыдущих уровней.
При несоблюдении основных предпосылок МНК приходится корректировать модель, изменяя ее спецификацию, добавлять (исключать) некоторые факторы, преобразовывать исходные данные для того, чтобы получить оценки коэффициентов регрессии, которые обладают свойством несмещенности, имеют меньшее значение дисперсии остатков и обеспечивают в связи с этим более эффективную статистическую проверку значимости параметров регрессии.
