Изменение параметров потока при прохождении через СУ. Потери энергии в СУ, способы уменьшения потерь энергии

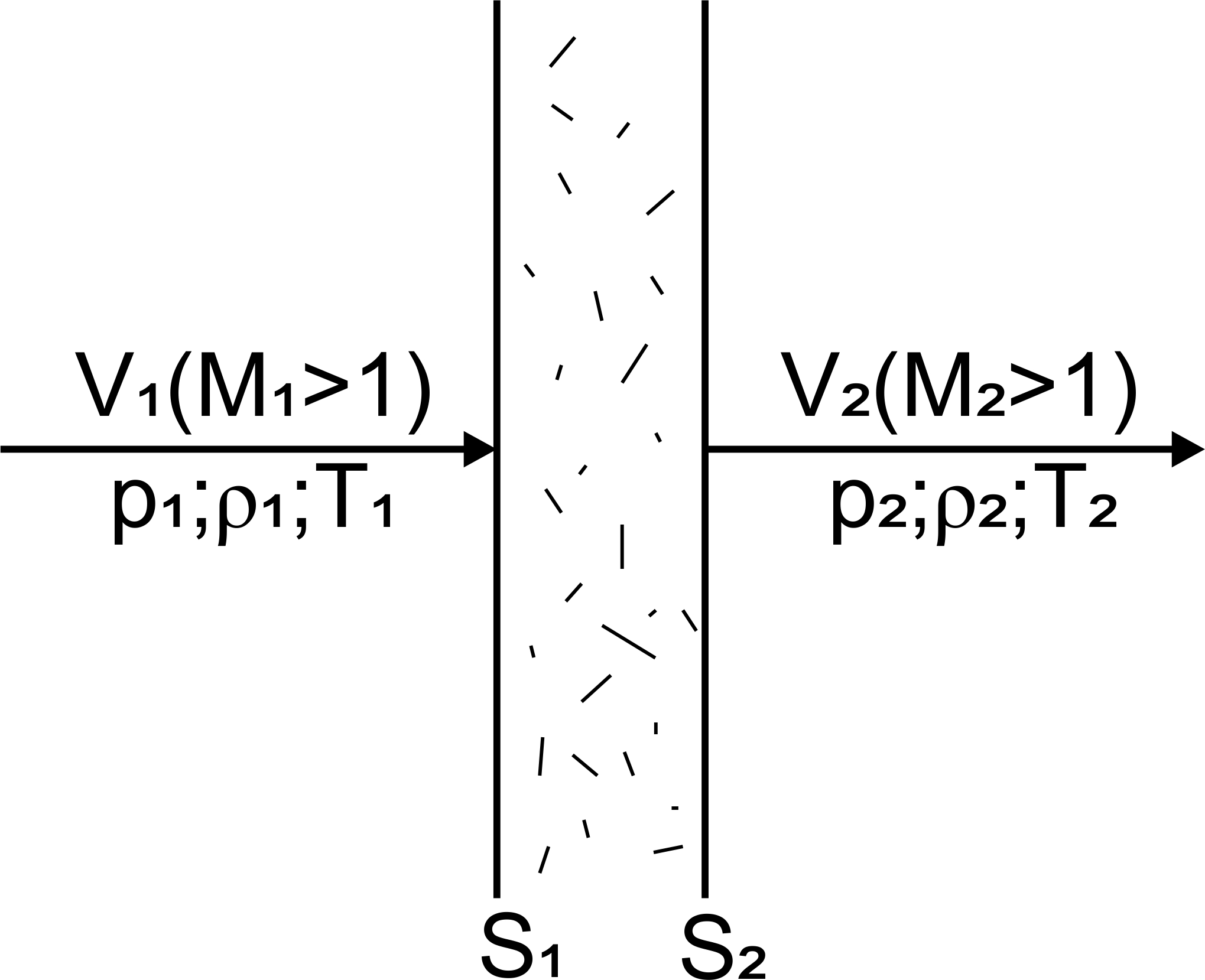
Рассмотрим прохождение потока через скачок уплотнения (рис.2.7). Так как толщина скачка очень мала ( 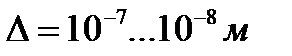), то будем считать что .

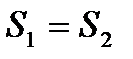Рис. 2.7 Изменение параметров потока при прохождении через скачок уплотнения

Используя уравнение неразрывности

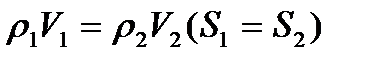, (2.2)

уравнение энергии:

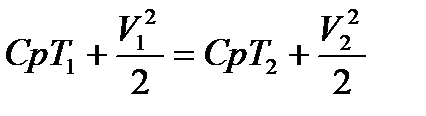, (2.3)

уравнение количества движения:

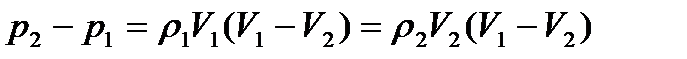. (2.4)

получим (без вывода) кинематическое соотношение для прямого скачка уплотнения:

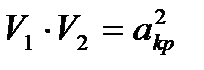, (2.5)

разделив на ,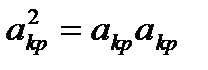

имеем

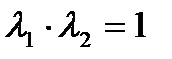, (2.6)

где 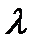- приведенная скорость .

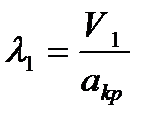Если 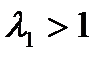, то из кинематического соотношения следует, что 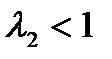. То есть на прямом скачке сверхзвуковое течение всегда переходит в дозвуковой поток.

Математически возможно обратное соотношение: если 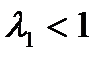, то из кинематического соотношения следует, что 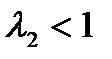. Однако, в природе скачков разрежения не существует.

Если кинематическое соотношение выражает связь между скоростями до и после скачка, то динамическое соотношение – связь термодинамических параметров (оно справедливо как для прямого, так и для косого скачков).

Используя те же уравнения (2.2 – 2.4) для получения динамического соотношения, имеем

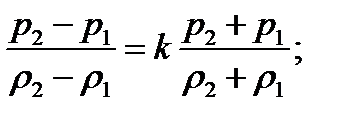(2.7)

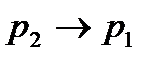Если , а 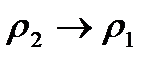, то мощность скачка уменьшается. Получим из левой части уравнения (2.7)

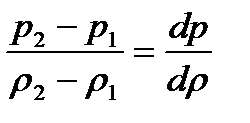, (2.8)

Или подставляя (2.8) в (2.7)

.

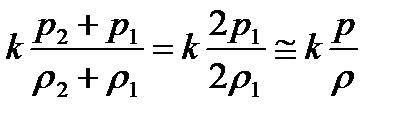Отсюда получим

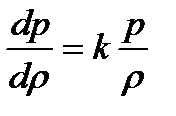. (2.9)

Полученная формула (2.9) – формула для квадрата скорости звука (для слабых возмущений)

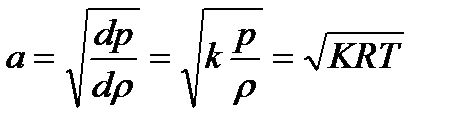. (2.10)

Значит, при уменьшении интенсивности СУ или ударных волн, они превращаются в слабые звуковые волны или малые возмущения.

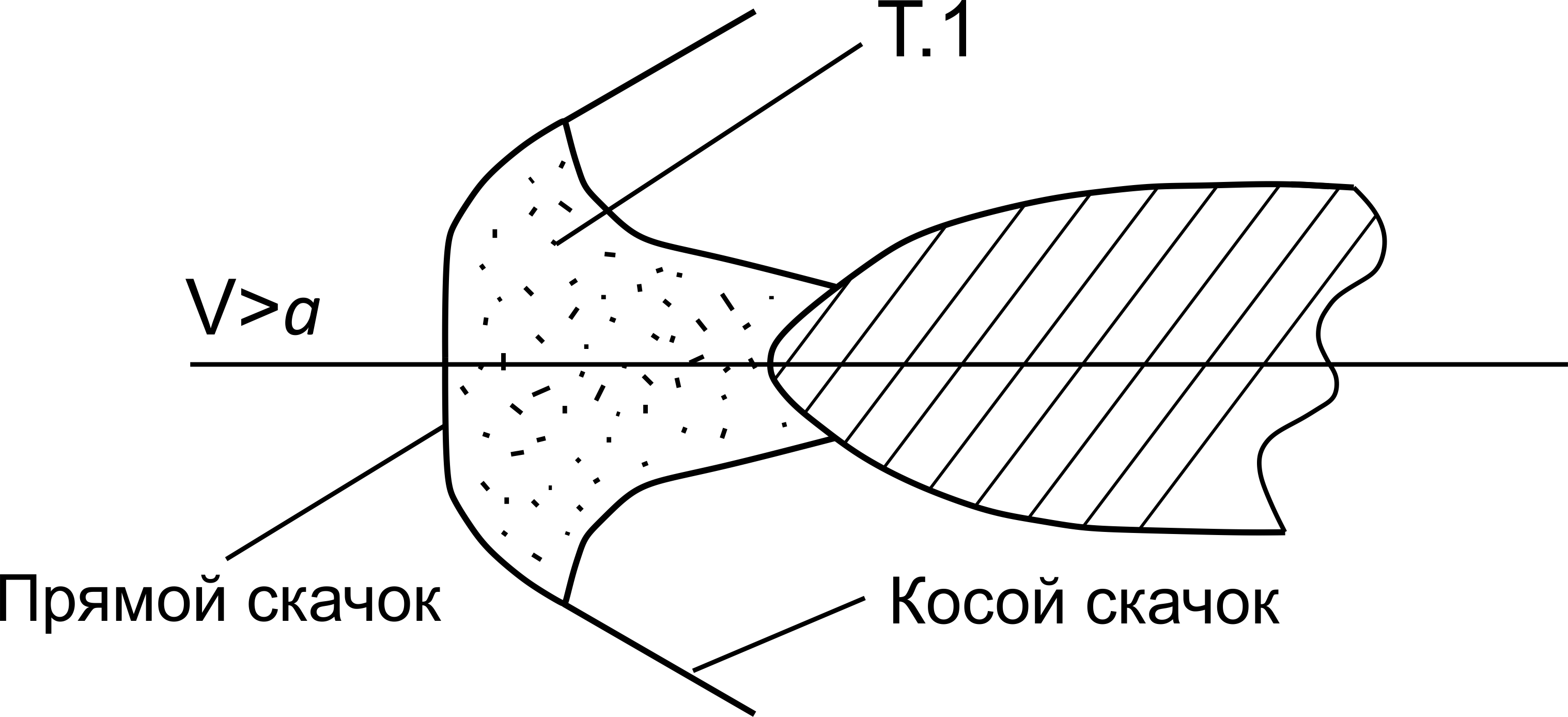
Появление СУ на поверхностях самолета приводит к значительным потерям полного давления (кинетической энергии) воздушного потока. При этом часть кинетической энергии воздуха используется на его сжатие, а другая переходит в тепло (необратимые тепловые потери). Это так называемая составляющая общего сопротивления – волновое сопротивление. Потери в прямом скачке уплотнения определяются резким торможением потока в скачке (рис.2.8), и необходимостью разворота струек при обтекании затупленного тела (например, обычного дозвукового профиля крыла).

При этом за прямым скачком (в точке Т1) поток дозвуковой (V < a), что определяется кинематическим соотношением (2.6).

В случае натекания на острую входную кромку (рис. 2.9) образуется уже косой СУ, и потери существенно меньше: такого резкого торможения струек не возникает, поток остается сверхзвуковым V > a (в точке Т2).

Рис. 2.8 Образование прямого СУ при натекании на затупленную кромку ВС

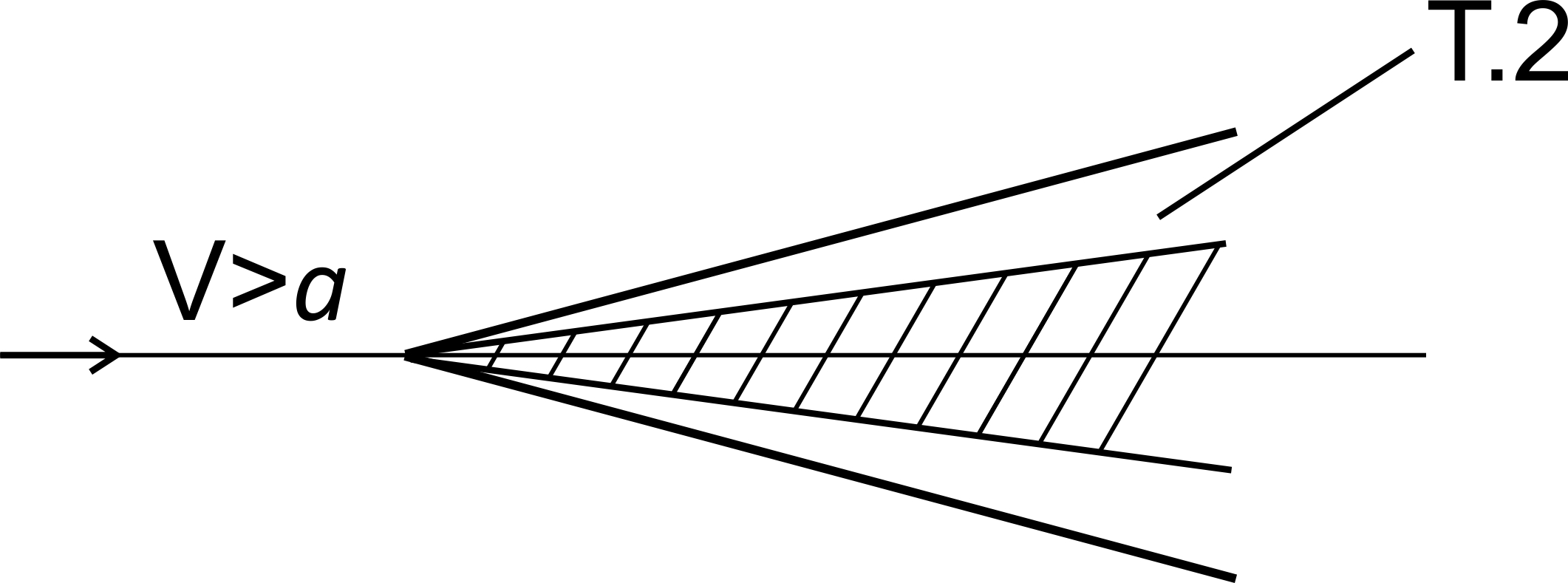
Рис. 2.9 Образование косого СУ при натекании на острую кромку ВС

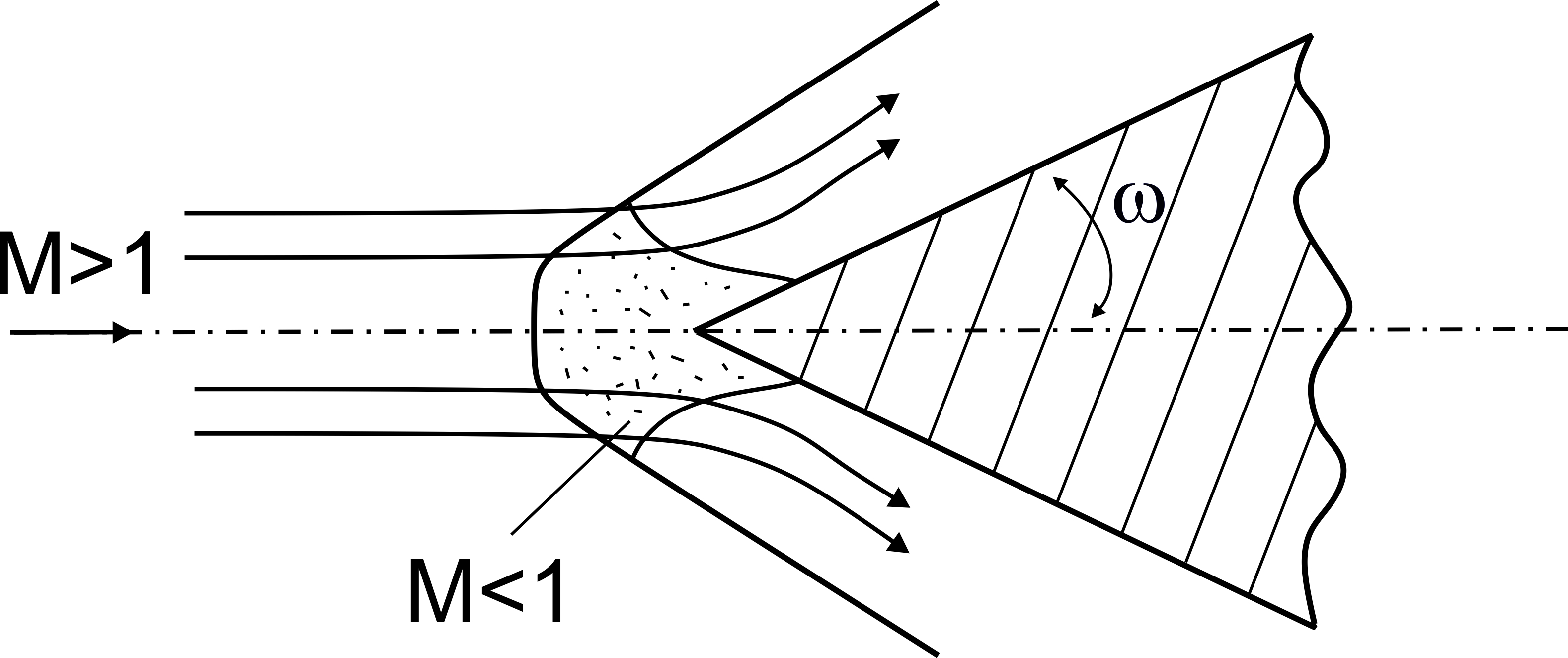
Однако, острые входные кромки ВС под большим углом конусности (рис. 2.10) образуют комбинированный СУ: комбинацию прямого (в средней части) и косого СУ. Здесь комбинированный скачок более мощный, чем один косой, и потери на нем также велики.

Рис. 2.10 Образование комбинированного СУ при натекании на острую кромку ВС

Для того, чтобы уменьшить мощность СУ, необходимо посадить скачок на острую кромку носовой части ВС или крыла. Последнее определяется критическим углом раствора конуса 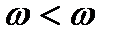_доп (или клина). В этом случае возникает присоединенный косой скачок, потери в котором меньше (рис. 2.9).

При полете с M<1,5 потери в СУ невелики. При M>1,5, чтобы уменьшить потери реализуют систему косых скачков, заканчивающуюся слабым прямым скачком. Конструктивно это достигается, например, установкой в диффузор ГТД центрального тела (рис. 2.11).

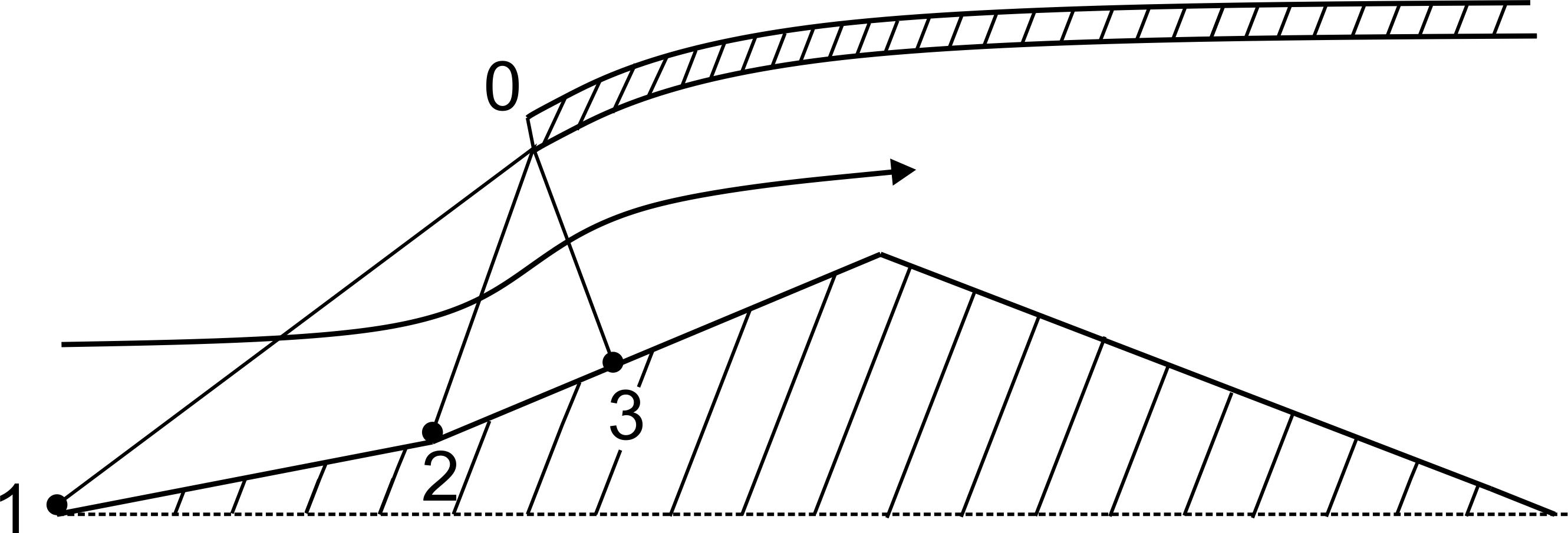
Рис. 2.11 Реализация системы косых СУ для уменьшения потерь