Множественная линейная регрессия

Значения экономических переменных определяются обычно вли­янием не одного, а нескольких объясняющих факторов. В таком случае зависимость y=f(x) означает, что х - вектор, содержащий т компонентов: х = (х₁, х₂, ... , х_m). Задача оценки статистической взаимосвязи переменных у и х = (х₁, х₂, ... , х_m) формулируется аналогично случаю парной регрессии. Записывается функция у = f(a,х)+e, где a - вектор параметров, e - случайная ошибка. По данным наблюдений выборки размерности n требуется оценить значения параметров a, то есть провести параметризацию выбранной формулы (спецификации) зависимости.

Мы будем говорить о линейной зависимости у от х, то есть о множественной линейной регрессии. Теоретическое уравнение рег­рессии имеет вид:

у = a₀+a₁х₁ +a₂х₂ + ... +a_mх_m + e.

Здесь a - вектор неизвестных параметров размерности (т + 1). Пусть имеется п наблюдений вектора х и зависимой переменной у. Для того, чтобы формально можно было решить задачу, то есть найти некоторый наилучший вектор параметров, должно быть п ³ т+1. Если это условие не выполняется, то можно найти бесконечно много разных векторов коэффициентов, при которых линейная формула связывает между собой х и у для имеющихся наблюдений абсолютно точно. Если, в частном случае, п = т+1 (например, при двух объясняющих переменных в уравнении у = a₀+a₁х₁ +a₂х₂ и трех наблюдениях), то оценки коэффициентов a рассчитываются един­ственным образом - путем решения системы линейных уравнений.

Функция ЛИНЕЙН()

Чтобы вычислить прямую линию, которая наилучшим образом аппроксимирует имеющиеся данные, используется статистическая функция ЛИНЕЙН(). Функция возвращает массив, который описывает полученную прямую. ЛИНЕЙН может также возвращать дополнительную регрессионную статистику. Отчет по регрессии располагается в заранее выделенном диапазоне ячеек следующим образом:

an	…	a2	a1	a0
sn	…	s2	s1	s0
R2	sey
F	k
SSreg	SSresid

se_y - Стандартная ошибка для оценки y.

F - F-статистика, или F-наблюдаемое значение. F-статистика используется для определения того, является ли наблюдаемая взаимосвязь между зависимой и независимой переменными случайной или нет.

k - Степени свободы. Степени свободы полезны для нахождения F-критических значений в статистической таблице. Для определения уровня надежности модели нужно сравнить значения в таблице с F-статистикой, возвращаемой функцией ЛИНЕЙН.

SSreg - Регрессионная сумма квадратов.

SSresid - Остаточная сумма квадратов.

Проводя регрессионный анализ, Microsoft Excel вычисляет для каждой точки квадрат разности между прогнозируемым значением y и фактическим значением y. Сумма этих квадратов разностей называется остаточной суммой квадратов. Затем Microsoft Excel подсчитывает сумму квадратов разностей между фактическими значениями y и средним значением y, которая называется общей суммой квадратов (регрессионная сумма квадратов + остаточная сумма квадратов). Чем меньше остаточная сумма квадратов по сравнению с общей суммой квадратов, тем больше значение коэффициента детерминации R², который показывает, насколько хорошо уравнение, полученное с помощью регрессионного анализа, объясняет взаимосвязи между переменными.

Пример 2. Используя множественный регрессионный анализ, оценить цену офисного здания в заданном районе на основе описанных переменных (см. пример1).

Выполнение.

Для нахождения уравнения регрессии с помощью функции ЛИНЕЙН() необходимо выполнить следующие шаги.

1. Озаглавьте область будущего отчета, введя в клетку G1: Регрессионный анализ. Выделите диапазон G2:K9. Размер диапазона выбирается следующим образом. Число строк – одна, если требуется получить только коэффициенты регрессии, пять, если необходимо получить дополнительную статистику. Число столбцов соответствует числу переменных.

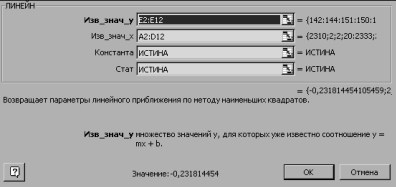
2. Выберите функцию ЛИНЕЙН() из раздела статистические и заполните окно диалога.

3. Диалоговое окно функции « ЛИНЕЙН»

Известные_значения_y - это множество значений y, которые уже известны (E2:E12).

Известные_значения_x - это множество значений x, которые уже известны для соотношения (A2:D12). Массив известные_значения_x может содержать одно или несколько множеств переменных при условии, что они имеют одинаковую размерность с массивом известные_значения_y.

Конст - это логическое значение, которое указывает, требуется ли, чтобы константа a₀ была равна 0. Если конст имеет значение ИСТИНА или опущено, то a₀ вычисляется обычным образом. Если конст имеет значение ЛОЖЬ, то a₀ полагается равным 0 и значения a₁ подбираются так, чтобы выполнялось соотношение y = a₁x.

Статистика - это логическое значение, которое указывает, требуется ли вернуть дополнительную статистику по регрессии. Если статистика имеет значение ИСТИНА, то функция ЛИНЕЙН возвращает дополнительную регрессионную статистику. Если статистика имеет значение ЛОЖЬ или опущена, то функция ЛИНЕЙН возвращает только коэффициенты a_i.

3. Функция ЛИНЕЙН() является формулой массива. Поэтому после заполнения окна диалога и нажатия ОК, необходимо комбинацией Shift-Ctrl-Enter завершить заполнение выделенного диапазона.

ЛИНЕЙН(E2:E12;A2:D12;ИСТИНА;ИСТИНА) возвращает следующие результаты.

-0,23181	2,7092	12,61839	0,025561	56,58702
0,013728	0,54907	0,413939	0,005618	12,66169
0,996544	1,004233	#Н/Д	#Н/Д	#Н/Д
432,4997		#Н/Д	#Н/Д	#Н/Д
1744,676	6,050904	#Н/Д	#Н/Д	#Н/Д

Теперь может быть получено уравнение множественной регрессии

y = a₁×x₁ + a₂×x₂ + a₃×x₃ + a₄×x₄ + a₀:

y = 0,03x₁ + 12,62x₂ + 2,71x₃ – 0,02x₄ + 56,59

По этому уравнению застройщик может определить оценочную стоимость здания под офис в том же районе, которое имеет площадь 2500 квадратных метров, три офиса, два входа, зданию 25 лет, используя следующее уравнение:

y = 0,03*2500 + 12,62*3 + 2,71*2 - 0,02*25 + 56,59 = 175,37 тыс.$.