Определение характеристик одноканальной СМО с ожиданием без ограничения на вместимость блока ожидания

Стационарный режим функционирования данной СМО существует при для любого и когда , система алгебраических уравнений, описывающих работу СМО при для любого , имеет вид:

(2.11)

Решение данной системы уравнений имеет вид:

,

(2.12)

где .

Определим характеристики одноканальной СМО с ожиданием, без ограничения на длину очереди:

– среднее число находящихся в системе клиентов (заявок) на обслуживание:

;

(2.13)

– средняя продолжительность пребывания клиента в системе:

;

(2.14)

– среднее число клиентов в очереди на обслуживание:

;

(2.15)

– средняя продолжительность пребывания клиента в очереди:

.

(2.16)

Аппаратура и материалы

Микрокалькулятор, программное обеспечение MS Excel.

Указания по технике безопасности

При выполнении работы студенты должны руководствоваться общими для учебных аудиторий правилами техники безопасности.

Методика и порядок выполнения работы

Согласно исходным данным (таблица 1.1), расчитать:

– вероятность отказа в обслуживании заявки;

– относительную пропускную способность;

– абсолютную пропускную способность;

– среднее число находящихся в системе заявок;

– среднее время пребывания заявки в системе;

– среднюю продолжительность пребывания клиента в очереди;

– среднее число заявок в очереди;

– Сделать выводы.

Содержание отчета и его форма

Отчет должен содержать:

6.1 Расчет вероятности отказа в обслуживании заявки;

6.2 Расчет относительной пропускной способности;

6.3 Расчет абсолютной пропускной способности;

6.4 Расчет среднего числа находящихся в системе заявок;

6.5 Расчет среднего времени пребывания заявки в системе;

6.6 Расчет средней продолжительности пребывания клиента в очереди;

6.7 Расчет среднего числа заявок в очереди;

6.8 Выводы.

Контрольные вопросы и защита работы

7.1 В чем сущность одноканальной системы массового обслуживания с ожиданием?

7.2 Каковы состояния одноканальной системы массового обслуживания с ожиданием?

7.3 Как будет описываться стационарный процесс в системе массового обслуживания с ожиданием?

7.4 В чем особенность одноканальной СМО с ожиданием без ограничения на вместимость блока ожидания?

7.5 Как будет описываться стационарный режим функционирования СМО с ожиданием без ограничения на вместимость блока ожидания?

Защита работы проводится в устной форме, состоит в предоставлении студентом правильно выполненного отчета по работе, коротком докладе и в ответах на вопросы, представленные выше.

Практическое занятие 14.

Определение характеристик многоканальной системы массового обслуживания с отказами

Цель и содержание

Цель работы – приобрести навыки моделирования многоканальной системы массового обслуживания с отказами.

В результате выполнения работы студенты должны:

1. Определить вероятность отказа в обслуживании заявки;

2. Определить относительную пропускную способность;

3. Определить абсолютную пропускную способность;

4. Определить среднее число каналов, занятых обслуживанием;

5. Сделать выводы.

Теоретическое обоснование

В подавляющем большинстве случаев на практике системы массового обслуживания являются многоканальными и, следовательно, модели с 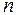обслуживающими каналами (где ), представляют несомненный интерес.

Процесс массового обслуживания, описываемый данной моделью, характеризуется интенсивностью входного потока 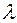, при этом параллельно может обслуживаться не более 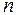клиентов (заявок). Средняя продолжительность обслуживания одной заявки равняется . Входной и выходной потоки являются пуассоновскими. Режим функционирования того или иного обслуживающего канала не влияет на режим функционирования других обслуживающих каналов системы. Причем, длительность процедуры обслуживания каждым из каналов является случайной величиной, подчиненной экспоненциальному закону распределения. Конечная цель использования 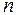параллельно включенных обслуживающих каналов заключается в повышении (по сравнению с одноканальной системой) скорости обслуживания требований за счет обслуживания одновременно клиентов.

Состояния данной СМО имеют следующую интерпретацию:

– все каналы свободны;

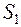– занят один канал, остальные свободны;

.................

– заняты ровно каналов, остальные свободны;

.................

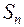– заняты все 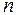каналов, заявка получает отказ в обслуживании.

Уравнения Колмогорова для вероятностей состояний системы ,..., , ..., будут иметь следующий вид:

(3.1)

Начальные условия решения системы:

, .

Стационарное решение системы имеет вид:

(3.2)

где .

Формулы для вычисления вероятностей называются формулами Эрланга.

Определим вероятностные характеристики функционирования многоканальной СМО с отказами в стационарном режиме:

– вероятность отказа:

,

(3.3)

т. к. заявка получает отказ, если приходит в момент, когда все 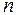каналов заняты. Величина характеризует полноту обслуживания входящего потока,

– вероятность того, что заявка будет принята к обслуживанию (она же – относительная пропускная способность системы 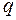) дополняет до единицы:

;

(3.4)

– абсолютная пропускная способность:

;

(3.5)

– среднее число каналов, занятых обслуживанием ( ):

.

(3.6)

Величина характеризует степень загрузки СМО.

Аппаратура и материалы

Микрокалькулятор, программное обеспечение MS Excel.