Потенциальная энергия деформации
Внешние силы, приложенные к упругому телу и вызывающие изменение геометрии тела, совершают работу W на соответствующих перемещениях. Одновременно с этим в упругом теле накапливается потенциальная энергия его деформирования U. При действии динамических внешних нагрузок часть работы внешних сил превращается в кинетическую энергию движения частиц тела К. Приняв энергетическое состояние системы до момента действия данных сил равным нулю, и в условиях отсутствия рассеивания энергии, уравнение баланса энергии можно записать в следующем виде:
W = U + K. (2.11)
При действии статических нагрузок К = 0, следовательно,
W = U. (2.12)
Это означает, что при статическом нагружении работа внешних сил полностью преобразуется в потенциальную энергию деформации. При разгрузке тела производится работа за счет потенциальной энергии деформации, накопленной телом. Таким образом, упругое тело является аккумулятором энергии. Это свойство упругого тела широко используется в технике, например, в заводных пружинах часовых механизмов, в амортизирующих рессорах и др. В случае простого растяжения (сжатия) для вывода необходимых расчетных зависимостей потенциальной энергии деформации рассмотрим решение следующей задачи.
На рис. 2.9, а изображен растягиваемый силой Р стержень, удлинение которого соответствует отрезку 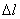 , ниже показан график изменения величины удлинения стержня
, ниже показан график изменения величины удлинения стержня 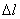 в зависимости от силы Р (рис. 2.9, б). В соответствии с законом Гука этот график носит линейный характер.
в зависимости от силы Р (рис. 2.9, б). В соответствии с законом Гука этот график носит линейный характер.
Пусть некоторому значению силы Р соответствует удлинение стержня 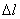 . Дадим некоторое приращение силе DР - соответствующее приращение удлинения составит
. Дадим некоторое приращение силе DР - соответствующее приращение удлинения составит 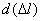 . Тогда элементарная работа на этом приращении удлинения составит:
. Тогда элементарная работа на этом приращении удлинения составит:
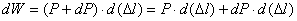 , (2.13)
, (2.13)

Рис.2.9
вторым слагаемым, в силу его малости, можно пренебречь, и тогда
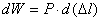 . (2.14)
. (2.14)
Полная работа равна сумме элементарных работ, тогда, при линейной зависимости “нагрузка - перемещение”, работа внешней силы Р на перемещении 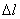 будет равна площади треугольника ОСВ (рис. 2.9), т.е.
будет равна площади треугольника ОСВ (рис. 2.9), т.е.
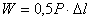 . (2.15)
. (2.15)
В свою очередь, когда напряжения 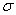 и деформации
и деформации 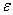 распределены по объему тела V равномерно (как в рассматриваемом случае) потенциальную энергию деформирования стержня можно записать в виде:
распределены по объему тела V равномерно (как в рассматриваемом случае) потенциальную энергию деформирования стержня можно записать в виде:
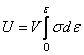 . (2.16)
. (2.16)
Поскольку, в данном случае имеем, что 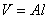 ,
, 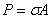 и
и 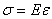 , то
, то
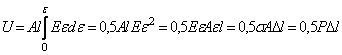 , (2.17)
, (2.17)
т.е. подтверждена справедливость (2.12).
С учетом (2.8) для однородного стержня с постоянным поперечным сечением и при Р = const из (2.17) получим:
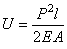 . (2.18)
. (2.18)
Единицей измерения потенциальной энергии деформации является 1Hм = 1Дж.
