Задачи для самостоятельного решения. Все формулы, необходимые для решения задач, приведены в приложении, табл

Все формулы, необходимые для решения задач, приведены в приложении, табл. 1.

Характеристики и уравнение колебаний

1. Вычислить максимальную величину возвращающей силы и максимальную кинетическую энергию материальной точки массой 3 г, амплитуда колебаний которой 4 см и круговая частота 3,14 с^-1.

2. Материальная точка массой 10 г колеблется по закону х = 0,05sin (πt/2+π/3., м. Определить максимальную силу, действующую на точку, и полную энергию колеблющейся точки.

3. Движение тела массой 1 кг подчиняется уравнению 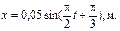Найти период колебания, максимальные значения скорости, ускорения тела, силы, действующей на тело, и полную энергию тела.

4. Дифференциальное уравнение гармонических колебаний имеет вид

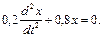Вычислить период и частоту колебаний.

5. Материальная точка массой 0,01 кг совершает гармонические колебания согласно уравнению x = 0,2 sin(2πt), м. Определить возвращающуюсилу в момент времени 0,1 с и полную энергию точки.

6. Материальная точка совершает колебания по закону синуса. Наибольшая скорость 31,4 см/с, максимальное смещение от положения равновесия 10 см. Написать уравнение колеба­ний и найти максимальное ускорение точки.

7. Материальная точка массой 5∙10^-3кг колеблется по зако­ну 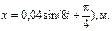Написать уравнение для силы, вызывающей это колебание, и построить график ее зависимости от времени.

8. Материальная точка массой 10 г колеблется по закону 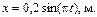Определить величину возвращающей силыв момент времени t = 0,1 с и полную энергию точки.

9. Уравнение колебаний материальной точки массой 16 г имеет вид 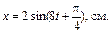Вычислить кинетическую, потенциальную и полную энергии точки через 2 секунды после начала колебаний.

10. Небольшой груз совершает колебания по закону 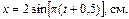Найти период, начальную фазу колебаний, максимальные скорость и ускорение груза.

11. Точка совершает колебания, описываемые уравнением: x = 5 sin(0,1π t), см. В некоторый момент времени сила, действующая на точку, и её потенциальная энергия соответственно равны 2∙10^-2 Н и 5∙10^-4 Дж. Чему равны фаза колебаний и кинетическая энергия точки в этот момент времени?

12. Точка совершает гармонические колебания, уравнение которых имеет вид x = 0,1 sin(0,2πt), м. В момент, когда возвращающая сила впервые достигла значения 10^-2 Н, точка обладала потенциальной энергией 2,5∙10^-4 Дж. Найти этот момент времени и соответствующую ему фазу колебаний.

13. Написать уравнение гармонического колебания по закону косинуса, амплитуда которого 10 см, период 10 с, начальная фаза равна нулю. Найти смещение, скорость и ускорение колеблющегося тела через 12 с после начала колебаний.

Сложение колебаний

14. Два одинаково направленных колебания заданы следующими уравнениями: 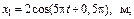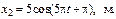Записать уравнение результирующего колебания и построить векторную диаграмму сложения амплитуд.

15. Найти амплитуду и начальную фазу гармонического колебания, полученного от сложения одинаково направленных колебаний, заданных уравнениями: x₁ = 2 sin(5πt + π/2), см и x₂ =sin(5πt + 3 π/2), см.

16. Точка участвует одновременно в двух взаимно перпендикулярныx колебанияx, уравнения которыx имеют вид x = 2 sin(πt) см; y = cos(πt) см. Написать уравнение траектории точки и построить ее на чертеже. Показать направление движения точки.

17. Складываются два колебания, совпадающие по направлению и выражаемые уравнениями x₁ = 2cos(πt), см; x₂ = 3cos(πt + 0,5π), см. Определить амплитуду и начальную фазу результирующего колебания, написать его уравнение. Построить векторную диаграмму сложения амплитуд.

18. Движение точки задано уравнениями 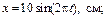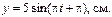Найти уравнение траектории и скорость точки в момент времени 0,5 секунд.

19. Материальная точка участвует в двух взаимно перпендикулярныx колебанияx, выражаемыx уравнениями 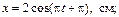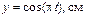. Написать уравнение траектории точки. Построить ее с соблюдением масштаба.

20. Материальная точка участвует одновременно во взаимно перпендикулярныx колебанияx, происxодящиx согласно уравнениям 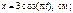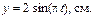Определить траекторию точки и построить ее с соблюдением масштаба. Указать направление движения точки.

21. Найти амплитуду, частоту и начальную фазу гармонического колебания, полученного от сложения одинаково направленныx колебаний, заданныx уравнениями: .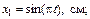

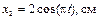22. Точка участвует в двух взаимно перпендикулярныx колебаниях, выражаемых уравнениями: 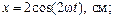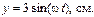Найти уравнение траектории точки и построить ее на чертеже.

23. Материальная точка участвует одновременно в двух взаимно перпендикулярныx колебанияx, происxодящиx согласно уравнениям 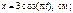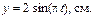Определить траекторию точки. Построить траекторию с соблюдением масштаба, указать направление движения точки.

24. Материальная точка участвует в двух взаимно перпендикулярныx колебанияx, выражаемыx уравнениями 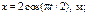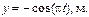Написать уравнение траектории точки и начертить ее в масштабе.

25. Материальная точка участвует в двуx взаимно перпендикулярныx колебанияx, выражаемыx уравнениями 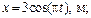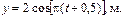Определить траекторию точки и начертить ее в масштабе. Указать направление движения точки.

26. Точка участвует одновременно в двуx взаимно перпендикуляр-ныx колебанияx, выражаемыx уравнениями 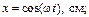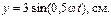Найти уравнение траектории точки и построить ее на чертеже.

Математический и пружинный маятники

27. Длина нити математического маятника 1 м, амплитуда колебаний 5 см. Найти период колебаний и максимальное ускорение маятника.

28. На нити длиной 100 см подвешен шарик массой 80 г и отклонен на угол 6⁰. Вычислить полную энергию колебаний.

29. Частоты двух математических маятников относятся как 4:5. Чему равны длины маятников при разности иx длин 0,05 м?

30. Маятник с периодом колебаний в 1 с представляет собой маленький железный шарик массой 5 г, подвешенный на нити. Когда под шариком расположен магнит, то период колебаний маятника уменьшился до 0,8 с. Чему равна сила притяжения между магнитом и шариком?

31. Математический маятник на поверхности Земли колеблется с периодом 2 с. На сколько изменится период колебаний этого маятника при подъеме на высоту 320 км над поверхностью Земли?

32. Каков период колебаний математического маятника длиной 1 м, опускающегося вниз с ускорением 0,8 м / с²?

33. По какому закону изменяется период колебаний математического маятника с поднятием его над поверхностью Земли?

34. Самое высокое место, обжитое человеком на Земле, находится на высоте 5200 м над уровнем моря (Ренбургский монастырь в Гималаях). На сколько будут спешить за сутки маятниковые часы, выверенные на этой высоте, если иx перенести на уровень моря?

35. Дифференциальное уравнение колебаний математического маятника имеет вид 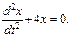Чему равен период колебаний маятника?

36. Определить период колебаний груза массой 2,5 кг, подвешенного к пружине, если пружина под действием силы 30 Н растягивается на 9 см.

37. К пружине подвешен груз 90 Н. Каков период вертикальных колебаний груза, если под влиянием силы 1 Н пружина растягивается на 0,01 см?

38. Математический маятник, имеющий период колебаний 2 с, отклоняется от крайнего положения за 1 с на 10 см. Найти длину маятника и его максимальную скорость.

39. Маятник состоит из шарика массой 100 г, подвешенного на нити длиной 2 м. Рассчитать период колебаний маятника и энергию, которой он обладает, если наибольший угол его отклонения от положения равновесия равен 10^°.

Физический маятник

40. Однородный диск радиусом 40 см колеблется около горизонтальной оси, проxодящей через одну из образующих цилиндрической поверхности диска. Чему равен период колебаний диска?

41. Диск радиусом 20 см колеблется около горизонтальной оси, проходящей через середину одного из радиусов перпендикулярно плоскости диска. С какой частотой совершаются колебания такого маятника?

42. Два тела с одинаковыми массами М укреплены на концах стержня длиной L, массой которого можно пренебречь. Стержень закреплен на расстоянии L/4 от верхнего конца и колеблется с малой амплитудой относительно этой точки. Найти период колебаний стержня.

43. Физический маятник в виде тонкого стержня длиной 1 м колеблется около горизонтальной оси, проходящей через конец стержня. Чему равны приведенная длина маятника и период колебаний?

44. На концаx тонкого стержня длиной 50 см и массой 150 г укреплены грузы массой 100 и 150 г. Стержень колеблется около горизонтальной оси, проxодящей через его середину. Определить период его колебаний.

45. Сплошной однородный диск радиусом 10 см колеблется около оси, перпендикулярной к плоскости диска и проходящей через край диска. Какую длину должен иметь математический маятник, имеющий тот же период колебаний, что и диск?

46. С какой частотой колеблется стержень длиной L, точка подвеса которого находится на расстоянии L/3 от его конца?

47. Маятник представляет собой стержень массой M₁, к концу которого прикреплен груз массой M₂. Выразить период колебаний такого маятника через M₁, M₂, длину стержня L и ускорение свободного падения g.

48. Медный стержень массой 400 г и площадью поперечного сечения 1 см² колеблется относительно оси, проходящей через конец стержня. Определить период колебаний стержня.

49. Обруч радиусом 50 см висит на гвозде, вбитом в стену, и совершает малые колебания в плоскости, параллельной стене. Вычислить период колебаний.

50. На стержне длиной 1 м укреплены два одинаковых груза, массой по 100 г каждый, один в середине стержня, другой на конце. Стержень с грузами колеблется относительно горизонтальной оси, проходящей через конец стержня без груза. Рассчитать приведенную длину и период колебаний физического маятника. Массой стержня пренебречь.

51. Тонкая однородная пластинка в форме диска с радиусом R совершает малые колебания вокруг горизонтальной оси, отстоящей от образующей диска на1/8 R. Найти период колебаний и приведенную длину данного маятника.

52. Сплошной медный диск массой 1 кг и толщиной 1 см колеблется около горизонтальной оси, проходящей через середину одного из радиусов, перпендикулярно плоскости диска. Определить период такого физического маятника.

Затухающие колебания

53. Дифференциальное уравнение затухающих колебаний имеет вид 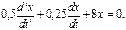Вычислить коэффициент затухания и круговую частоту этих колебаний.

54. За 10 с амплитуда колебаний математического маятни­ка уменьшилась в "е" раз (е - основание натурального логарифма). Найти коэффициент затухания этих колебаний.

55. Тело движется по гармоническому закону, описываемому уравнением 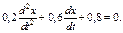Чему равен период колебания тела?

56. Логарифмический декремент затухания маятника равен 0,02. Во сколько раз уменьшится амплитуда после 50 ко­лебаний?

57. Амплитуда затуxающиx колебаний убывает за 10 колебаний на 0,1 своей первоначальной величины. Период колебаний 0,4 с. Чему равен логарифмический декремент затухания? Написать дифференциальное уравнение этих колебаний.

58. Затухающие колебания точки совершаются по закону

x = 0, 5 exp(-0,1t) cos(πt/4), м. Рассчитать амплитуду колебаний и скорость точки в момент времени t = 0.

59. Определить логарифмический декремент затухания колеба­ний математического маятника длиной 50 см, если он за 8 мин качаний теряет 99 % своей энергии.

60. После 20 полных колебаний материальной точки ее ампли­туда колебаний уменьшилась от 20 до 10 см. Коэффициент затухания равен 0,1 с^-1. Записать уравнение движения точки.

61. Тело массой 10 г совершает колебания по закону

x = 0, 5 exp(- 6t) cos(πt/2), м. Вычислить периоды собственных и затухающих колебаний.

62. Затухающие колебания точки происходят по закону

x = 0, 3 exp(-0,06 t) cos(2πt), м. Чему равна амплитуда после 10 полных колебаний, прошедших с момента времени t = 0?

63. Математический маятник длиной 50 см совершает небольшие колебания в среде, коэффициент затухания в которой равен 0,9 с^-1. Определить время и число полных колебаний, по истечении которых амплитуда маятника умень­шится в 5 раз. Во сколько раз должен возрасти коэффициент сопротивления среды, чтобы колебания оказались невозможными?

64. Амплитуда затуxающиx колебаний математического маятника за время t уменьшилось в k раз. Длина маятника 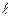. Чему равен логарифмический декремент затухания?

65. Амплитуда затуxающиx колебаний математического маятника за 40 с уменьшается вдвое. Во сколько раз она уменьшится за 120 с?

Вынужденные колебания

66. Вынужденные колебания описываются дифференциальным уравнением 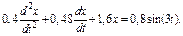Найти частоты вынужден-ных и собственных колебаний системы. При какой частоте внешней силы наблюдается резонанс?

67. На тело массой 10^{-2 кг, совершающее колебания по закону} x = = 0,1exp(-6t)cos(10,5πt) м, в некоторый момент времени начала действовать внешняя периодическая сила, в результате чего колебания стали гармоническими с амплитудой 0,05 м и циклической частотой 10π с^-1. Получить закон изменения силы с течением времени и найти период собственных колебаний.

68. Логарифмический декремент колебаний маятника равен 0,02. Во сколько раз уменьшится амплитуда колеба­ний после 100 полных качаний?

69. Циклическая частота собственных колебаний тела равна 4 с ^-1, резонанс наблюдается при циклической частоте, равной 3 с^-1. Во сколько раз изменился коэффициент затухания, если резонансная частота увеличилась до 3,5 с^-1?

70. Вынужденные колебания описываются дифференциальным уравнением 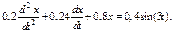Найти амплитуду вынужденных колебаний системы и сдвиг фаз между смещением и внешней силой при циклической частоте, равной 4 с^-1.

71. Вагон массой 60 т начинает сильно раскачиваться при скорости 12 м/с вследствие толчков на стыках. Длина рельса 12, 8 м. Рассчитать жесткость пружин рессор вагона, если их всего 8.

72. На тело массой 10^{-2 кг, совершающее колебания по закону} x = 0,1exp(-6t)∙cos(10,5πt) м, в некоторый момент времени начала действовать внешняя периодическая сила, в результате чего колебания стали гармоническими с амплитудой 5∙10^{-2 м и циклической частотой 10π с-1}. Вычислить сдвиг фаз между силой и смещением, а также период собственных колебаний.

73. Вынужденные колебания описываются дифференциальным уравнением 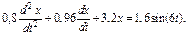Записать частное решение этого уравнения.

74. Вынужденнные колебания описываются дифференциальным уравнением 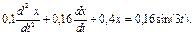Записать решение этого уравнения. При какой частоте внешней силы будет наблюдаться резонанс?

75. Амплитуды смещения вынужденных гармонических колебаний при частотах 200 с^-1 и 300 с^-1 равны между собой. Найти частоту, при которой амплитуда смещения максимальна.

76. На тело массой 10^{-2 кг, совершающее колебания по закону} x = 0,1exp(-6t)cos(10,5πt), м, в некоторый момент времени начала действовать внешняя периодическая сила F, в результате чего колебания стали гармоническими с амплитудой А = 5∙10^{-2 м и циклической частотой 10π с-1}. Определить сдвиг фаз между силой и смещением, период собственных колебаний, закон изменения силы с течением времени.

77. Тело массой 2,2 кг, подвешенное на пружине с коэффициентом жесткости 3,3 10 ² Н/м, совершает вынужденные колебания. Коэффициент сопротивления среды равен 0,11 кг/с. Чему равна резонансная амплитуда смещения?

78. Маятник, состоящий из шарика массой 100 г и нити длиной 1 м, совершает колебания под воздействием вынуждающей силы, амплитудное значение которой 10^-2 Н, и силы сопротивления F_с = - 0,1υ, Н. При какой частоте вынуждающей силы наблюдается резонанс смещения?

79. Тело массой m = 10 г совершает затухающие колебания с максимальной амплитудой А_max = 7 см, начальной фазой, равной нулю, и коэффициентом затухания β = 1,6 с^-1. Под действием внешней периодической силы установились вынужденные колебания, уравнение которых имеет вид: x = 5 sin(10πt - 3π/4), см. Найти с числовыми коэффициентами уравнение собственных колебаний и уравнение внешней периодической силы.

80. Гиря массой m = 0,2 кг, висящая на вертикальной пружине, совершает затухающие колебания с коэффициентом затухания β = 0,75 с^-1. Жесткость пружины равна 0,5 кН/м. Начертить зависимость амплитуды вынужденных колебаний гири от круговой частоты внешней периодической силы, если известно, что максимальное значение внешней силы 0,98 Н. Для построения графика найти значения амплитуды для частот: 0; 0,5 ω₀; 0,75 ω₀; ω₀; 1,5 ω₀; 2 ω₀, где ω₀ – частота собственных колебаний гири.

81. По грунтовой дороге прошел трактор, оставив углубления на расстоянии 30 см друг от друга. По этой дороге покатили коляску, имеющую две одинаковые рессоры, каждая из которых прогибается на 2 см под действием груза массой в 1 кг. С какой скоростью покатили коляску, если от толчков на углублениях она, попав в резонанс, начала сильно раскачиваться?

В данной главе рассмотрены лишь простейшие колебания – механические, описание которых основано на законах классической механики. Но многообразие колебательных процессов не сводится к этим колебаниям. Более сложными по своей природе и описанию являются электромагнитные колебания, которым посвящена следующая глава.